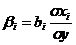Задачи КРА, условия применения

Условия применения корреляционно-регрессионного анализа (КРА).

1 - достаточно большой объем статистической совокупности.

2 - объем совокупности должен быть в 6-8 раз (идеально в 10 раз) больше,

числа факторов включаемых в анализ.

3 - изучаемая совокупность должна быть однородна.

4 - признаки включаемые в анализ должны иметь количественное выражение

(возможно включение фиктивных переменных по атрибутивному признаку).

5 - методы корреляции и регрессии ориентированы на закон нормального распределения.

Комплексный корреляционно-регрессионный анализа предполагает:

1 - глубокий теоретический анализ изучаемого объекта или процесса, в ходе которого выявляются внешние и внутренние связи и зависимости, определяются факторы влияющие на состояние и изменение изучаемого объекта.

2 - на основе элементарных статистических приемов выдвигается гипотеза о наличии или отсутствии корреляционной зависимости между исследуемыми признаками.

3 - на основе показателей корреляции делается вывод о наличии или

отсутствии статистически значимых связей и зависимостей.

4 - на основе уравнения регрессии оценивается сила влияния признаков-факторов на результат, осуществляемый ранжирование факторов по силе влияния на результат.

5 - практическое использование результатов КРА и прогнозирование на основе регрессионных моделей.

Перечисленные задачи решаются с использованием корреляции и регрессии.

Поскольку, у этих методов одна общая цель и много общих вычислительных процедур, анализ проводимый с их использованием называется корреляционно-регрессионный анализ (КРА).

Приемами, которыми позволяют выдвинуть гипотезу о наличии или

отсутствии связей:

1 - построение параллельных рядов.

2 - построение групповых и корреляционных таблиц (небольшая

неоднородная групповая таблица).

3 - построение поля корреляции (графическое изображение корреляционной зависимости).

ОХ - значение признака-фактора.

ОУ - значение признака-результата.

. .

. · .

· . · ·

· . .

· ·

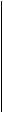
Точки на графике соответствуют значению признака-результата при конкретном значении признака-фактора.

На основании изображения поля корреляции, можно сделать предположение о направленности корреляционной зависимости, о наличии или отсутствии связи, а также о степени тесноты корреляционной зависимости, о форме зависимости.

. . . · . · . . · . · . · · · . . ..

. · . · . . · . . · . . · . · . · ·. .

· . · · · . . · . · . · . . .· .· . .· ·.

· . . · . · . · . · . · . . · · ·. . .· ·

· · . . · · · ·. · · ·

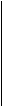
прямая обратная нелинейная зависимость

зависимость зависимость зависимость отсутствует

Практические задачи, решаемые с помощью корреляционно-регрессионный анализа (КРА):

1 - наличие причинно-следственной связи, однозначно определяется зависимая переменная (т.е. признак-результат), и независимая переменная (т.е. признак-фактор).

признак-результат - следствие (объем пр-ва)

признак-фактор - причина (производительность)

2 - наличие взаимосвязи между признаками, изменение одного признака ведет к изменению другого признака, но при этом однозначно не определить, что причина, а что следствие.

3 - наличие ложной корреляции. Ложная корреляция - параллельное изменение двух признаков обусловленное одновременным влиянием на них третьего признака.

Показатели тесноты связи.

Показатели корреляции позволяют подтвердить или опровергнуть наличие корреляционной зависимости между изучаемыми признаками, а также измерить степень тесноты корреляционной зависимости.

Первый коэффициент корреляции - парный коэффициент корреляции Пирсена.

Коэффициент корреляции строится исходя из оценки совместного варьирования двух признаков.

(yi-y)*(xi-x) - среднее произведение этих признаков - ковариация.

Показатель ковариации трудно интерпретировать содержательно, поэтому на практике статистического анализа практически не используется.

Путем стандартизации показатели ковариации получаем коэффициент корреляции Пирсена.

r- коэффициент корреляции Пирсена.

r=[å(yi-y)*(xi-x)/n*6y*6x]

r=(yi*xi-x*у)/(6y*6x)

Парный коэффициент корреляции изменяется в пределах от 0 до 1 по модулю (0£|х|£1)

Коэффициент корреляции может быть отрицательным и положительным.

Знак коэффициента корреляции характеризует направленность зависимостей.

Если коэффициент корреляции отрицательный, то зависимость между изучаемыми признаками обратная.

Если коэффициент корреляции положительный, то зависимость между изучаемыми признаками прямая.

Близость коэффициента корреляции к нулю означает отсутствие связи.

Близость коэффициента корреляции к единице означает, что связь тесная.

Если коэффициент корреляции равен единице, то связь функциональная.

0£|r|£0,3 - связь практически отсутствует

0,3£|r|£0,5 - связь заметная

0,5£|r|£0,7 - связь умеренная

|r|>0,7 - связь тесная

Значимость коэффициента корреляции от объема изучаемых признаков.

(28. Множественный и частный коэффициент)Парный коэффициент корреляции оценивает тесноту связи между парой признаков. При изучении множественной зависимости множественный коэффициент корреляции, кот. характеризует степень тесноты связей между признаком-результатом или некоторыми признаками-факторами.

r - коэффициент детерминации, характеризует долю объясненной дисперсии признака-результата.

Объясненная дисперсия - факторная дисперсия, т.е. дисперсия признака-результата обусловленная вариацией признака-фактора.

r =0,78, т.е. вариация оборота продукции на 78% связано с производительностью труда.

При двухфакторной модели связей множественный коэффициент корреляции - Ry1x1x2

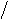2 2 2 2 2 2

Ry1x1x2=Ö(rух1+rух2-2rух1*rух2*rх1х2)/(1-rх1х2)

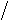Если число анализируемых факторов больше 2, то множественный коэффициент корреляции

2 2

Ry1x1x2xn=Ösф/sобщ

На основе факторной и общей дисперсии.

R - множественный коэффициент детерминации, характеризует долю объемной (факторной) дисперсии, результативного признака в общей дисперсии признака-результата.

Множественный коэффициент корреляции изменяется в пределах от 0 до 1.

При изучении множественной корреляционной зависимости часто возникает необходимость рассчитать частные коэффициенты корреляции, которые оценивают степень тесноты с одним из анализируемым фактором при условии эллеминирования влияния других факторов, включенных в анализ.

Эллеминирование выполняется путем закрепления значений фактора на определенном (как правило на среднем уровне) уровне.

При изучении двухфакторной корреляционной зависимости рассчитывают 2 коэффициента частной корреляции.

2 2

Ryx1,x2=(ryx1-ryx2*rx1x2)/[(1-ryx2)*(1-rx1x2)

Данный коэффициент оценивает тесноту зависимости у от х1 при условии эллеминирования (х2).

2 2

Ryx2,x1=(ryx2-ryx1*rx1x2)/[(1-ryx1)*(1-rx1x2)

Оценивает тесноту связи между (у) и фактором (х2), при условии эллеминирования влияния фактора х(1).

Рассмотренные выше коэффициенты корреляции дают надежные оценки при наличии линейной зависимости между признаком-результатом и признаками-факторами.

Если связь между изучаемыми признаками нелинейная, то при оценке тесноты связи предпочтение следует отдать показателю корреляционному отношению.

Если корреляционное отношение считается по результатам регрессионного анализа, то оно называется теоретическое.

Если по результатам аналитической группировки: эмпирическое.

Теоретическое корреляционное отношение - это отношение факторной дисперсии к общей дисперсии результативного признака.

2 2

h=sфакт/sобщ

2 2

sобщ=å(yi-y)/n

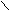2 2

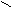
sфакт=å(yi-y)/n

у- теоретическое значение

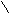
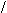2 2

sост=å(yi-y)/n

Остаточная дисперсия - это дисперсия признака-результата обусловленная прочими факторами не включенными в анализ.

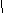
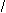
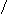2 2

h=Öå(yi-y)/å(yi-y)

Теоретически корреляции изменилась от 0 до1. Чем ближе значение корреляционного отношения к 1, тем теснее зависимость между изучаемыми признаками.

h - коэффициент детерминации и характеризует долю дисперсионного результативного признака, объясненную вариацией анализируемого признака-фактора, т.к. рассчитывается как отношение дисперсии факторной к общей результативного признака.

Эмпирическое корреляционное отношение рассчитывается по данным аналитической группировки, как отношение межгрупповой дисперсии к общей дисперсии результативного признака.

Сравнивая значение коэффициента корреляции с теоретическим корреляционным отношением можно сделать вывод о правомерности использования уравнения линейной зависимости для описания связи между изучаемыми признаками, т.к. в условиях линейной зависимости величина коэффициента корреляции относительно совпадает.

Индекс корреляции (r)- показывает тесноты связи.

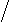2 2

r=Ö1-sост/sобщ

Расчет показателя вариации следует предварять анализам корреляционного поля с целью выявления «выбросов».

Если на поле корреляции выделяются 2 и более группы, то говорят, что в изучаемой совокупности присутствуют кластеринг.

В этом случае совокупность разбивается на группы (кластеринг) показывается корреляции и анализ ведется в разрезе отдельных групп.

Парная линейная регрессия.

Задачи: регрессионный анализ лежит в сфере установленных форм зависимости, определенными факторами регрессии, использования уравнения для оценки неизвестных значений зависимой переменной.

у - признак-результат, зависимая переменная

х - признак-фактор, независимая переменная

Существует достаточно важная характеристика связей с точки зрения взаимодействия фактора.

Если характерная связь 2-х признаков - парная, если более 2-х - множественная.

(30 вопрос)Для характерного изменения влияния (х) на вариацию (у) служат методы регрессионного анализа.

В случае парной линейной зависимости строится регрессионная модель: yi=a0+a1xi+еi, где i=1,...,n

n-число наблюдений;

а0, а1 - неизвестные характеристики уравнения;

еi- ошибка случайной переменной (у).

При подстановки (х) получаем парное уравнение регрессии.

уiтеор=a0+a1xi

уiтеор- рассчитанное значение результативного признака;

а0, а1 - рассчитанные с помощью значений различных мат. методов и процедур. Наиболее распространен - метод наибольших квадратов.

Оценки а0, а1 наименьшим образом получаются когда å(yi-yiтеор)®min

Сумма квадратов отклонения эмпирических значений зависимых переменных от вычисления по уравнению регрессии должны ®min.

dF/da=0

dF/da0=0

2 2

a1=(ху-х*у)*/х-(х)

2 2 2

х-(х)=sх

Форма представляется в виде уравнения регрессии.

Уравнение регрессии - определенная математическая функция, которая описывает связь между зависимой и независимой переменной.

Простейший вид уравнения регрессии - парная линейная регрессия.

у=а+bх

у - признак-результат (зависимая переменная)

х - признак-фактор (независимая переменная)

а, b - параметры уравнения.

Эта запись предполагает, что значение признака-результата (у) полностью определяются значениями признака-фактора (х).

у=а+bхi+ei

ei - ошибка (остаток) регрессии

Если на поле координат нанести поле корреляции в виде точек, координаты которого определяются значениями признака-результата и признака-фактора у каждой единиц совокупности. (69 квартир, т.е. 69 точек) И построить линию регрессии.

ei - разница между фактическими и теоретическими значениями у.

ei - разница по вертикали между точкой на поле корреляции и точкой на линии регрессии.

Т.к. в соц.-экон. явлениях функциональная зависимость отсутствует, то ошибка выборки уравнения регрессии будет всегда.

Парная регрессия широко используется на практике (как и парная корреляции), т.к. часто имеется фактор доминирующий среди множества факторов определяющих признак-результат, а также нередко возникает необходимость оценить влияние одного конкретного фактора.

Чтобы воспользоваться уравнением регрессии нужно рассчитать его параметры.

Самый распространенный метод вычисления параметров регрессии - метод наименьших квадратов (МНК).

Суть МНК - удается получить такие значения параметров, при которых минимизируется сумма квадратов отклонений расчетных или теоретических значений признака-результата от их фактических значений.

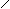2

S=å(yi-y)®min

Рассмотрим S как f(a,b) проводят дифференцирование приравнивая частичные производные к нулю и строят систему нормальных уравнений.

df/da=0 df/db=0

Решение системы нормальных уравнений позволяет найти параметры a и b.

2

b=(x*y-x*y)/sx

sx - дисперсия признака-фактора.

у=а-bх

Пример: при оценке зарплаты от величины прожиточного минимума.

у=0,77+0,92х ® (0,77 - а, 0,92 - b)

у - зарплата по регионам

х - величина прожиточного минимума

Параметр а - содержательно не интерпретируется.

Параметр b - коэффициент регрессии и характеризует на сколько единиц своего измерения изменяется признак-результат при изменении признака фактора на 1 своего измерения.

0,92 - при изменении величины прожиточного минимума на 1 рубль, величина зарплаты увеличится на 92 копейки.

Знак при коэффициенте регрессии характеризует направленность зависимости.

(+) - зависимость прямая

(-) - зависимость обратная

Множественная регрессия.

Построение уравнения множественной регрессии обусловлено ожиданием на изучаемые социально-экономические явления изучением нескольких факторов и желанием исследователя оценить их совокупное влияние на изучаемое явление. Общая запись:

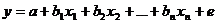
n – число факторов

Параметры фактора называются условно чистыми. Их можно было бы назвать чистыми, если бы в уравнение можно было включить все факторы, определяющие признак результат. Но, как правило, это невозможно, т.к. число факторов (х) включенных в анализ ограничивается объектом изучаемой совокупности, а также могут быть факторы, влияние которых просто неизвестно.

Чистые коэффициенты регрессии интерпретируются аналогично парным коэффициентам регрессии, но их значения не совпадают. Несовпадение коэффициентов парной и множественной регрессии для одних и тех же факторов обусловленных тем что в парной регрессии не учитывается связь между факторами, и если фактор(площадь кухни) тесно связан с фактором (площадь квартиры), то в уравнении парной регрессии при оценке одного фактора учитывается другой.

Коэф. регресси во множ. регрессии характеризует влияние конкретного фактора на результат при условии, что остальные факторы останутся неизменными, т.е. их влияние иллюстрируется, т.е. во множ. уравнение мы получаем очищенную оценку влияния конкурентного фактора.

Коэф. регрессии характеризует силу связи между (х) и (у).

При построение уравнения множ. Регрессии имеется возможность ранжировать факторы по степени их влияния на (у), однако (х) – именованные величины, и могут быть выражены в разных единицах измерения, следовательно, непосредственно ранжированы быть не могут.

Возможность оценить и ранжировать (у) дает переход к относительным характеристикам, в качестве которых могут быть использованы так называемые 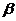- коэффициенты или коэффициент эластичности(Е). 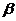- коэффициенты используются для построение уравнения регрессии стандартном виде. Он раскладывается как коэф. регрессии умноженный на отношение среднеквадратического отклонения (х) на среднеквадратическое отклонение (у). Е- коэф-т рассчитывается: