Полная группа событий. Ее отличия от ПЭС.

ТЕОРИЯ ВЕРОЯТНОСТЕЙ.

Пространство элементарных событий. Примеры.

Множество всех взаимоисключающих исходов опыта называют ПЭС.

Кидают монетку. ПЭС – это герб или решка.

Четные или нечетные числа.

Свойства событий.

- Перестановочные свойства

A+B=B+A A+(B+C)=(A+B)+C

AB=BA A(BC)=(AB)C

- Свойства константы поглощения

A+Ω=Ω AΩ=A

A+Ø=A AØ=Ø

Ø+Ω=Ω ØΩ=Ø

- Свойства дополнений

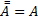
Ā+A=Ω

Ā•A=Ø

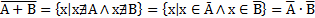
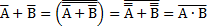
- Свойства разности

A-B=A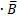

A-B={x|x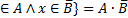

- Симметрическая разность

A∆B={x|(x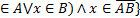

(A+B)•(Ā+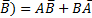

- Дистрибутивные

A(B+C)=AB+AC

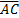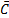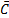A(B-C)=AB-AC AB-AC=AB· =AB(Ā+ )=AB =А(В-С)

Операции над событиями.

- сумма событий

C=A+B состоит из исходов, входящих или в А, или в B, или в A и B

- произведение событий

C=AB состоит из исходов, одновременно входящих в A и B

- разность событий

C=A-B состоит из исходов, входящих в A, но не входящих в B

- симметрическая разность

С=A∆B состоит из исходов, входящих либо в А, либо в B, но не входящих в AB

- дополнение

События делят на достоверные и обозначают Ω

Невозможное обозначается ᴓ

Случайное – A,B, C..

Пусть дана Ω и A – его подмножество

Дополнение A – это разность Ω и A

Полная группа событий. Ее отличия от ПЭС.

Пусть дана система событий попарносовместных и такая, что сумма событий равна Ω, такая система называется полной группой.

Совместность и несовместность событий. Несовместность в совокупности.

Пусть даны два события A и B. Они несовместны, если их произведение есть невозможное событие.

Пусть дана система событий {A₁, A₂, ..., A_n} будем говорить, что события этой системы попарно несовместны, если для любых i,k: A_i•A_k=Ø; i≠k

Пусть дана системы событий. Будем говорить, что она несовместима в совокупности, если произведение A₁•A₂•...•A_n=Ø

Модель классической вероятности. Свойства классической вероятности.

Пусть дано пространство Ω и функция p: пространство вещественных чисел

Ω: p: ΩàR Ω={w₁…w_n}

Свойства:

1. p(w_i)≥0 любое w_i?Ω

2. p(w₁)+…+p(w_n)=1

Свойства:

1. Вероятность достоверного

p(Ω)=cardΩ/cardΩ=1

2. Вероятность не возможного

p(Ø)=cardØ/cardΩ=0/cardΩ=0

3. Два не совместных события

AB=Ø

à p(AB)=card(A+B)/cardΩ=cardA/cardΩ+cardB/cardΩ=p(A)+p(B)

4. Два совместных события

AB=Ø

p(A+B)=card(A+B)/cardΩ=cardA+cardB-cardAB / cardΩ=p(A)+p(B)-p(AB)

5. Событие A инициазирует событие B

AсB à p(A)≤p(B)

6. Следует из предыдущих свойств

p(A)?[0,1]

7. p(Ā)=1-p(A)

Элементы комбинаторики - перестановки, сочетание, размещение

Количество всех возможных перестановок набора из n элементов - n-факториал.

Пусть дан набор из n элементов, то поднаборы из m элементов выбраны из исходных n и отличающиеся между собой только составом элементов, называют сочетаниями из n по m:

Пусть дан набор из n элементов, то поднаборы из m элементов, взятые из исходных n, отличающиеся между собой не только составом, но и порядком внутри, называют размещения ми из n по m:

Геометрическая вероятность. Примеры.

Если вероятность попадания случайно брошенной материальной точки на некоторый объект qсΩ не зависит от расположения области q в Ω, а определяется только ее мерой, то такая вероятность называется геометрической и определяется:

Теорема умножения событий.

A₁, A₂, … , A_n ? δ-алгебра

p(A₁ • A₂ • … • A_n)=p(A₁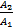)•p( )•p( 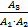)•…•p( )

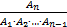Схема испытаний Бернулли.

Система независимых испытаний, где в каждом опыте системы события появляются с постоянной вероятностью, называют схемой испытаний Бернулли:

P_n(m)= 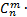p^m q^n-m

ТЕОРИЯ ВЕРОЯТНОСТЕЙ.

Пространство элементарных событий. Примеры.

Множество всех взаимоисключающих исходов опыта называют ПЭС.

Кидают монетку. ПЭС – это герб или решка.

Четные или нечетные числа.

Свойства событий.

- Перестановочные свойства

A+B=B+A A+(B+C)=(A+B)+C

AB=BA A(BC)=(AB)C

- Свойства константы поглощения

A+Ω=Ω AΩ=A

A+Ø=A AØ=Ø

Ø+Ω=Ω ØΩ=Ø

- Свойства дополнений

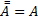
Ā+A=Ω

Ā•A=Ø

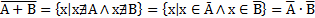
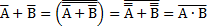
- Свойства разности

A-B=A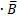

A-B={x|x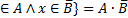

- Симметрическая разность

A∆B={x|(x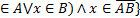

(A+B)•(Ā+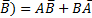

- Дистрибутивные

A(B+C)=AB+AC

A(B-C)=AB-AC AB-AC=AB· 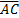=AB(Ā+ 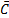)=AB 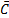=А(В-С)

Операции над событиями.

- сумма событий

C=A+B состоит из исходов, входящих или в А, или в B, или в A и B

- произведение событий

C=AB состоит из исходов, одновременно входящих в A и B

- разность событий

C=A-B состоит из исходов, входящих в A, но не входящих в B

- симметрическая разность

С=A∆B состоит из исходов, входящих либо в А, либо в B, но не входящих в AB

- дополнение

События делят на достоверные и обозначают Ω

Невозможное обозначается ᴓ

Случайное – A,B, C..

Пусть дана Ω и A – его подмножество

Дополнение A – это разность Ω и A

Полная группа событий. Ее отличия от ПЭС.

Пусть дана система событий попарносовместных и такая, что сумма событий равна Ω, такая система называется полной группой.