Вырожденное распределение и его характеристики.

Случайная величина ξ имеет вырожденное распределение с параметром а, и пишут ξ Î I_a если ξ принимает единственное значение а с вероятностью 1, то есть P(ξ=a) =1.

1) F(x)= 0 при x<a ; 1 при x³a.

2) x=a=const Þ M(x)=a; D(x)=0. Вырожденное распределение является моделью идеального измерительного прибора.

Дать определение распределению Бернулли.

Случайная величина ξ имеет распределение Бернулли с параметром р, и пишут ξÎ В_р, если ξ принимает значения 1 и 0 с вероятностями р и 1-р, соответственно. Случайная величина ξ с таким распределением равна числу успехов в одном испытании схемы Бернулли с вероятностью успеха (0 успехов или 1 успех).

Вычислить МО и дисперсию СВ. имеющей распределение Бернулли.

Таблица распределения ξ имеет вид

ξ
Р	(1-p)	p

Мат. ожидание в единичном испытании равно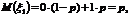

дисперсия: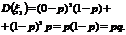

Дать определение биномиального распределения.

Говорят, что случайная величина ξ имеет биномиальное распределение с параметрами n и p, где 0£ p£ n и пишут ξ Î В_n,р, если ξ принимает значения 0, 1, …,n с вероятностями P(ξ = k) = C_n^k p^k (1-p)^n-k . Случайная величина ξ с таким распределением имеет смысл числа успехов в n испытаниях схемы Бернулли с вероятностью успеха р .

Таблица распределения ξ имеет вид

Как связаны биномиальное распределение и распределение Бернулли?

1. СВ x₁, распределённая по закону Бернулли, есть частный случай СВ с биномиальным законом распределения при n=1,.

2. В свою очередь, СВ x_n представляет собой сумму n одинаковых независимых СВ, идентичных x₁ . Поскольку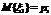

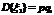
то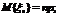

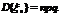
Вычислить мат. ожидание СВ., имеющей биномиальное распределение.

1). ξ₁ – СВ Бернулли

2). ξ_k - независимые, одинаково распределенные.

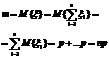
Вычислить дисперсию СВ, имеющей биномиальное распределение.

На основе выше сказанного (условия)

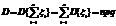
Дать определение распределения Пуассона.

Случайная величина ξ имеет распределение Пуассона с параметром λ, где λ > 0, и ξ Î П_λ, если ξ принимает значения 0, 1, 2 … с вероятностями

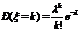
где λ – параметр распределения Пуассона. Это предельный случай биномиального распределения. (n®¥, p®0; np®l), при этом M(x)=np®l, D(x)=np(1-p)®l.

Таблица распределения ξ имеет вид

k				…
P(x=k)	e-l	le-l	l2e-l/2!	…

Вычислить мат. ожидание величины имеющей распределение Пуассона.

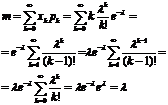
Записать формулу плотности вероятности нормального распределения. Нарисовать ее график.

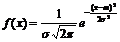
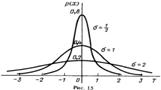
Записать формулу функции распределения нормального распределения. Нарисовать ее график.

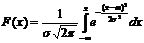
Как определяется функция Лапласа? Нарисовать ее график.

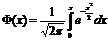
при х>5 [email protected]

Перечислить основные св-ва функции Лапласа.

1. Функция Лапласа нечётная.

2. Функция Лапласа монотонно возрастающая.

3. F(¥)= 0.5

4. F(-¥)= -0.5

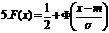
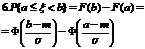
Выразить функцию распределения гауссовой случайной величины через функцию Лапласа.

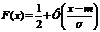
Сформулировать правило 3х сигм.

При однократном испытании значение гауссовой СВ. попадут в интервал m±3s с вероятностью, практически равной 1 (@0.997).