Как различаются детерминированные и случайные явления?
СЛУЧАЙНЫЕ ЯВЛЕНИЯ
‘’кгнннннннн
Как различаются детерминированные и случайные явления?
Зафиксируем комплекс внешних условий S и проведём эксперимент, который заключается в многократном измерении величины x. Если результат всегда повторяется (его можно предсказать со 100% точностью), то явление называется детерминированным, если результаты различны, то явление называется случайным.
2. Привести примеры детерминированных и случайных величин.
Одна и та же физическая величина в зависимости от решаемой задачи может быть принята детерминированной или случайной:
если мы рассматриваем погрешность номинала резистора, то мы принимаем сопротивление резисторов как случайную величину, а если мы достаём резистор из коробки с резисторами разных номиналов и рассматриваем вероятность получения резистора того или иного номинала, то в таком случае мы принимаем их сопротивление как детерминированную величину.
Что такое массовые случайные явления?
К массовым относят такие случайные явления, эксперимент с которыми можно провести неограниченное число раз.
4. Привести примеры массовых случайных величин.
Измерения сопротивления нескольких резисторов, подбрасывание монетки, извлечение разноцветных шаров из урны.
Как определяется частота исхода?
Частота исхода А:
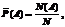
где N(A) – число выпадений А, а N-общее число проведенных экспериментов.
Почему частота исхода является случайной величиной?
Потому что она наперёд неизвестна.
Сформулировать свойство устойчивости частот.
,
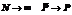где P – вероятность исхода, не является случайной величиной.
Дать определение равновозможных исходов.
Равновозможными (равновероятными) называются такие исходы, вероятности которых равны в силу реальной симметрии условий эксперимента.
Как определяется классическая вероятность?
Проведём эксперимент с n равно-возможными исходами w1,w2…wn. Тогда
,
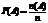где n(A) – число исходов, благоприятствующих событию А.
Когда можно использовать формулу классической вероятности?
Когда все исходы равновероятные и их число конечное.
11. Что такое урновая схема? Привести примеры.
Урновая схема применяется, когда речь идет об извлечении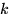 
объектов (шариков, карт и пр.) из урны (контейнера, колоды и пр.), содержащей 
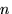объектов. При этом различают четыре схемы извлечения объектов: с возвращением и с учетом порядка, без возвращения и с учетом порядка, а также без возвращения без учета порядка и без возвращения без учета порядка.
Чему равно количество выборок в урновой схеме без возвращения?
Выбор без возвращения и без учета порядка - число сочетаний из n элементов по k элементов:
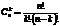
Выбор без возвращения, с учетом порядка - число размещений из n элементов по k элементов.
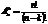
СЛУЧАЙНЫЕ СОБЫТИЯ
Какими бывают ПЭС?
Конечными (ограниченное число элементов, которые можно пересчитать); счётными (бесконечное число элементов, которые можно пронумеровать) и несчётными (неограниченное число элементов, которые невозможно пронумеровать).
18. Привести примеры конечных ПЭС.
Из урны с 3 белыми и 2 чёрными шариками наудачу извлекают 2 шарика.
ПЭС эксперимента: {ББ, БЧ, ЧБ, ЧЧ} – если порядок извлечения имеет значение, или
{ББ, ЧБ, ЧЧ} – если порядок извлечения не имеет значения.
Проводится однократное бросание монетки.
{Г, Р}
Проводится однократное бросание кубика.
{1, 2, 3, 4, 5, 6}
19. Привести примеры счётных ПЭС.
Производится бросание монеты до первого выпадения герба.
{Г, РГ, РРГ, …, Р…РГ, …}
Производится стрельба по мишени до первого попадания.
{По, ПрПо, ПрПрПо, …, Пр…ПрПо}
Из множества натуральных чисел выбирают одно.
{1, 2, 3, 4, …}
20. Привести примеры несчётных ПЭС.
Производится стрельба по мишени, попадание гарантировано.
{(х,у) х2 + у2 <= R2}
Производится стрельба по мишени, попадание не гарантировано.
{(х,у) х, у Є (-¥; +¥)}
ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
УСЛОВНАЯ ВЕРОЯТНОСТЬ
Привести формулу Байеса.
Доказать формулу Байеса.
Требуется найти вероятность события 
, если известно что В произошло. Согласно теореме умножения имеем:
.
Отсюда
; используя формулу полной вероятности, находим 
НЕЗАВИСИМЫЕ ИСПЫТАНИЯ.
72.Привести пример независимых испытаний.
Примером является Урновая схема с возвращением
Что такое схема Бернулли?
Схемой Бернулли называется последовательность n независимых испытаний в каждом из которых может осуществляться A или Ā, причем вероятность успеха не изменяется в процессе испытаний.
74. Привести пример последовательности испытаний, описанных схемой Бернулли.
Многократное бросание кости, при котором успехом считается выпадание 5 или 6 (вероятность успеха p=1/3)
Записать формулу Бернулли.
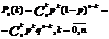
Обосновать ответ.
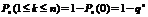
Противоположное событие – неуспех в каждом из n испытаний, вероятность qn
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.
СЛУЧАЙНЫЙ ВЕКТОР.
ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН.
130. Сформулировать задачу преобразования СВ.
По ФР F(x1,x2,…xn) совокупности СВ (x1,x2,…,xn) определить ФР F(y1,y2,…yk) величин h1=f1(x1,x2,…,xn),h2=f2(x1,x2,…,xn),…, hk=fk(x1,x2,…,xn)
131 Привести общий подход к решению задачи преобразования случайной величины
Искомая функция распределения определяется равенством
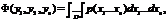D: {fi(x1,x2,…,xn)<yi, i=1..k}
В случае дискретных СВ решение даётся с помощью n-мерной суммы, также распространённой на область D.
Какой смысл имеет МО СВ?
МО – среднее значение СВ, которое не всегда совпадает с каким-то значением дискретной СВ.
Как определяется дисперсия
Дисперсия D(ξ) = M(ξ–M(ξ))2 есть «среднее значение квадрата отклонения СВ ξ от своего среднего.
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ.
Математическая статистика.
СЛУЧАЙНЫЕ ЯВЛЕНИЯ
‘’кгнннннннн
Как различаются детерминированные и случайные явления?
Зафиксируем комплекс внешних условий S и проведём эксперимент, который заключается в многократном измерении величины x. Если результат всегда повторяется (его можно предсказать со 100% точностью), то явление называется детерминированным, если результаты различны, то явление называется случайным.
2. Привести примеры детерминированных и случайных величин.
Одна и та же физическая величина в зависимости от решаемой задачи может быть принята детерминированной или случайной:
если мы рассматриваем погрешность номинала резистора, то мы принимаем сопротивление резисторов как случайную величину, а если мы достаём резистор из коробки с резисторами разных номиналов и рассматриваем вероятность получения резистора того или иного номинала, то в таком случае мы принимаем их сопротивление как детерминированную величину.