Математическое ожидание функции одного случайного аргумента.

Пусть Y = φ(X) – функция случайного аргумента Х, и требуется найти ее математическое ожидание, зная закон распределения Х.

1) Если Х – дискретная случайная величина, то

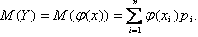
Пример 3. Найдем M(Y) для примера 1: M(Y) = 47·0,1 + 69·0,2 + 95·0,3 + 125·0,4 = 97.

2) Если Х – непрерывная случайная величина, то M(Y) можно искать по-разному. Если известна плотность распределения g(y), то

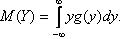
Если же g(y) найти сложно, то можно использовать известную плотность распределения f(x):

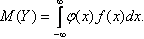
В частности, если все значения Х принадлежат промежутку (а, b), то

№37 Ф-я двух случ аргументов, закон расп-я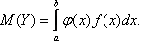

Если каждой паре возможных значений случайных величин Х и Y соответ-ствует одно возможное значение случайной величины Z, то Z называют функцией двух случайных аргументов X и Y : Z = φ(X, Y).

Рассмотрим в качестве такой функции сумму Х + Y. В некоторых случаях можно найти ее закон распределения, зная законы распределения слагаемых.

1) Если X и Y – дискретные независимые случайные величины, то для определения закона распределения Z = Х + Y нужно найти все возможные значения Z и соответствующие им вероятности.

3) Если X и Y – непрерывные независимые случайные величины, то, если плотность вероятно-сти хотя бы одного из аргументов задана на (-∞, ∞) одной формулой, то плотность суммы g(z) можно найти по формулам

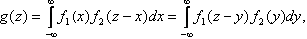
где f₁(x), f₂(y) – плотности распределения слагаемых. Если возможные значения аргументов неотрицательны, то

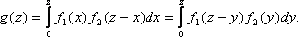
Замечание. Плотность распределения суммы двух независимых случайных величин называют композицией.

№38 Закон больших чисел: неравенство Чебышева

Вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине меньше положительного числа не меньше чем :

p( | X — M(X)| < ε ) ≥ D(X) / ε².

Доказательство. Пусть Х задается рядом распределения

Х х1 х2 … хп р р1 р2 … рп	х1	х2	…	хп
р	р1	р2	…	рп

Так как события |X — M(X)| < ε и |X — M(X)| ≥ ε противоположны, то р ( |X — M(X)| < ε ) + + р ( |X — M(X)| ≥ ε ) = 1, следовательно, р ( |X — M(X)| < ε ) = 1 - р ( |X — M(X)| ≥ ε ). Найдем р ( |X — M(X)| ≥ ε ).

D(X) = (x₁ — M(X))²p₁ + (x₂ — M(X))²p₂ + … + (x_n — M(X))²p_n . Исключим из этой суммы те слагаемые, для которых |X — M(X)| < ε. При этом сумма может только уменьшиться, так как все входящие в нее слагаемые неотрицательны. Для определенности будем считать, что отброшены первые k слагаемых. Тогда

D(X) ≥ (x_k+1 — M(X))²p_k+1 + (x_k+2 — M(X))²p_k+2 + … + (x_n — M(X))²p_n ≥ ε² (p_k+1 + p_k+2 + … + p_n).

Отметим, что p_k+1 + p_k+2 + … + p_n есть вероятность того, что |X — M(X)| ≥ ε, так как это сумма вероятностей всех возможных значений Х, для которых это неравенство справедливо. Следовательно, D(X) ≥ ε² р(|X — M(X)| ≥ ε), или р (|X — M(X)| ≥ ε) ≤ D(X) / ε². Тогда вероятность противоположного события p( | X — M(X)| < ε ) ≥ D(X) / ε², что и требо-валось доказать.

№39 Теоремы Чебышева и Бернули

Теоремы Чебышева и Бернулли.

Рассмотрим последовательность случайных величин 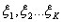(2).

Введем среднее арифметическое: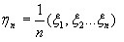

Запишем математическое ожидание: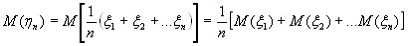

Обозначим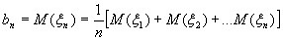

Def: говорят, что для последовательности выполняется закон больших чисел, если для любого 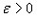справедливо равенство: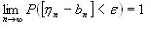

О равенстве (3) также говорят, что среднее арифметическое случайных величин в вероятностном смысле (по вероятности) сходится к среднему арифметическому их математических ожиданий.

Если последовательность случайных величин (2) удовлетворяет закону больших чисел, то, как видно из равенства (3), среднее арифметическое ведет себя фактически как величина неслучайная, поскольку ее значение в вероятностном смысле как угодно мало отличается от числа (среднего арифметического математического ожидания случайной величины ).

Теорема Чебышева: пусть случайные величины последовательности (2) таковы, что:

1) Они попарно независимы.

2) Имеют конечное математическое ожидание.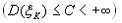

3) Имеют равномерно ограниченные дисперсии

Тогда к последовательности применим закон больших чисел.

Доказательство.

Оценим дисперсию: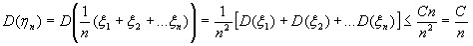

Применим неравенство (1):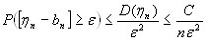

Левую часть выразим через вероятность противоположного события: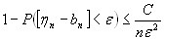

Умножим обе части на (-1):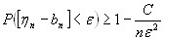

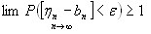
С другой стороны: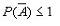

На основании двух предыдущих формул получаем формулу (3)

Теорема Бернулли: относительная частота события “А” в вероятностном смысле сходится к вероятности этого события:

(4)

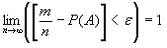
Доказательство.

С каждым испытанием свяжем случайную величину .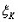

Тогда число наступлений события “А” в “n” независимых испытаний будет равно: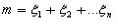

Покажем, что к этой последовательности применим закон больших чисел (равенство 3). Проверим выполнение условий теоремы Чебышева:

1) 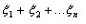– попарно независимы.

2)

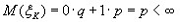
3)

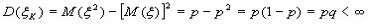
Таким образом в силу теоремы Чебышева к последовательности случайных величин { 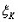} применим закон больших чисел, выражаемый равенством (3). В данном случае среднее арифметическое: 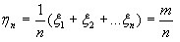– относительная частота.

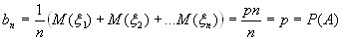В силу (3) получаем равенство (4).

№40 Оценка отклонения распределения НСВ от нормального коэффициента ассиметрии и эксцесса

Коэффициент асимметрии задает степень асимметричности плотности вероятности относительно оси, проходящий через ее центр тяжести. Коэффициент асимметрии определяется третьим центральным моментом распределения. В любом симметричном распределении с нулевым математическиможиданием, например, нормальным, все нечетные моменты, в том числе итретий, равны нулю, поэтому коэффициент асимметрии тоже равен нулю.
Степень сглаженности плотности вероятности в окрестности главного максимума задается еще одной величиной - коэффициентом эксцесса. Он показывает, насколько острую вершину имеет плотность вероятности по сравнению с нормальным распределением. Если коэффициент эксцесса большенуля, то распределение имеет более острую вершину, чем распределениеГаусса, если меньше нуля, то более плоскую.
Для расчета коэффициентов асимметрии и эксцесса в MathCAD имеютсядве встроенные функции.
- kurt (x) - коэффициент эксцесса (kurtosis) выборки случайных данных х;
- skew(x) - коэффициент асимметрии (skewness) выборки случайных данных X .

№41 Распределение «хи-квадрат»

Пусть х₁,х₂,…,х_n-независ. Норм.расп-е случ.величины с нулевым матем.ожиданием и сред.квадрат.отклонением=1,тогда закон расп-я суммы кварт.величин(Х-квадрат) х²=х₁ ²+х₂²+…+х_n² назв. Законом Х-квадрат с nстепенями свободы. Плотность расп-я этого закона опред:

0, при х<0

f(x) (e^-x/2*x^n/2-1)/2^n/2+Г’(n/2)^x ≥0

№42 распределение Стьюдента

Пусть х₀,х₁,…,х_n-независ. Норм.расп-е случ.величины с нулевым матем.ожиданием и сред.квадрат.отклонением=1, тогда величина опред по ф-ле:Т=( х₀/SÖ^m_n=1*x²/n) назв. Величиной имеющей расп-е Стьюдента с n-степенями свободы

Плотность имеет вид f(x)= b_n(1+ x²/2)^-((n+1)/n)

b_n=Г((n+1)/2)/Гn/2*pÖn

№43 Распределение Фишера-Снедекора

Пусть х₁,х₂,…,х_n ,у₁,у₂,…,у_n независ. Норм.расп-е случ.величины с нулевым матем.ожиданием и сред.квадрат.отклонением=1, тогда случ величина ,заданная ф-лой F_nm=((Sx_i ²/n)/S y_j ²/m) назв. Случ величиной, имеющей расп-е Фишера-Снедекора с n и m степенями свободы, плотность расп-я имеет вид

F(x)= 0,при x£0

C₀ *(x^(n-2)/2/(n+n x^(p+2)/2),для х>0

C₀=Г(((n+m)/2)*n^n/2 *m ^m/2 ))Г ^n/2Г ^m/2

№44 Система двух случайных величин. Закон расп-я.Ф-я расп-я. Свойства функции расп-я

Законом расп-я назв перечень возможных значений двумерн величины , т.е А(x_i,у_i) и их соотв. Вероятностей Р(x_i,у_i). Обычно закон задают таблицей с двойным ходом.1строка-все возможн.значения. составляющие х.1 столбец- все возможн.значения. составляющие у клетки на их пересечении (x_i,у_i) заполняют соответств. Вероятность , причем кол-вл знач-й х,у могут быть различными, т.к событие х=у_i и у=у_i образуют полную группу , то сумма вероятностей помещенных во всех клетках =1.

Ф-я расп-я:

Пусть х,у пара действительных чисел, вероятность события состоит в том, что составляющая х примет знач-е меньше х; составляющая у примет знач-е меньше у. X<x; Y<y. обозначение Р(X<x; Y<y)=F(x;y) – ф-я расп-я

Свойства функции расп-я

1.Значения ф-и расп-я удовлетв. Неравенству 0< F(x;y)<1

2. Ф-я F(x;y) явл. Неубывающей ф-ей.

3. Имеют место след соотношения:1)F(-∞; y)=0 2) F(x;-∞)=0 3) F(-∞;-∞)=0 4) F(+∞;+∞)=1

4. При у=∞, ф-я расп-я с-мы становиться ф-ей расп-я составляющей х. При х=∞, ф-я расп-я с-мы становиться ф-ей расп-я составляющей у

№45 Система двух случайных величин: плотность совместного расп-я вероятностей, нахождение ф-и расп-я по плотности расп-я, свойства двумерной плотности расп-я

Плотность совм.расп-я вероятностей назв частную производную второго порядка, смешанная по переменным х, у