Понятие плотности распределения, функция плотности НСВ

Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f (х) - первую производную от функции распределения F (х): f (х)= F'(х)

Из этого определения следует, что функция распре­деления F(х) является первообразной для плотности распре­деления f (х): F(х)=ò f (х).

Функцию f (х) можно называть дифференциальной функцией

Таким образом, зная интегральную функцию (функцию распределения) можно найти дифференциальную функцию(функцию плотности) и наоборот по формулам:f (х)= F'(х) F(х)=ò f (х).

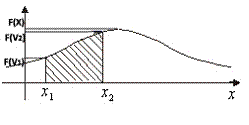
Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл

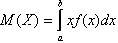
Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:

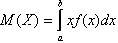
При этом, конечно, предполагается, что несобственный интеграл сходится.
Свойства математического ожидания НСВ аналогичны свойствам математического ожидания ДСВ.

Дисперсией непрерывной случайной величины называется математическое ожидание квадрата ее отклонения.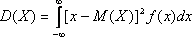

По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется формула:

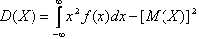
№32 Нормальное расп-е

Это такое расп-е случ.велечины Х, плотность Р которого опис. Формулой f(x)=(1/d(x)*Ö2p)*exp(-(x-M(x)² )/(2d²(x), где d(х)- сред.квадрат.отклонение, М(х)-матем.ожидание

№33 Нормальное расп-е: 1)вероятность попадания в заданный интервал, вероятность заданого отклонения

1)Если случайная величина Х задана плотностью распределения f(x), то вероятность того, что Х примет значение, принадлежащее заданному интервалу, вычисляется по формуле . Подставив в формулу значение плотности распределения из для нормального распределения N(a, s) и сделав ряд преобразований, вероятность того, что Х примет значение, принадлежащее заданному интервалу [x₁, x₂], будет равна:

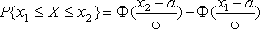Где а-мат.ожидание

2)

P (|X–a| ≤ e) = 2Ф(e/s) = 2Ф(t), где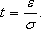

№34 Показательное расп-е НСВ: график, ф-я расп-я, плотность расп-я, матем ожидание, дисперсия

№35 Показательное расп-е: ф-я надежности, показательный закон надежности, характеристичесткое свойство этого закона

Функция надежности

Будем называть элементом некоторое устройство независимо от того, "простое" оно или "сложное".

Пусть элемент начинает работать в момент времени t₀=0, а по истечении времени длительностью t происходит отказ. Обозначим через Т непрерывную случайную величину - длительность времени безотказной работы элемента. Если элемент проработал безотказно (до наступления отказа) время, меньшее t то, следовательно, за время длитель­ностью t наступит отказ.

Таким образом, функция распределения F (t)=P(T<t) определяет вероятность отказа за время длитель­ностью t. Следовательно, вероятность безотказной работы за это же время длительностью t, т. е. вероятность про­тивоположного события Т > t, равна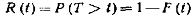

Функцией надежности R (t) называют функцию, определяющую надежность работы элемента за время длительностью t: