Аналитическое продолжение Г-функции.
F(z),f(z) аналитична в D1D1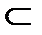 
D в D1 функции неразличимы 
F(z) аналитически продолжает f(z) на D
F(z)=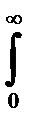 
e-ttz-1dt= 
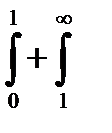e-t= 
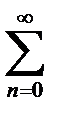(-1)tn/(n)! |tz-1|=tx-1ограничена
F1=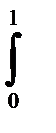 
e-ttz-1dt= 
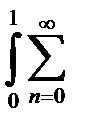(-1)ntn+z-1/(n)! dt= 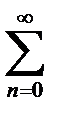(-1)n/(n)!*tn+z/n+z|01=
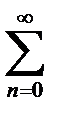= (-1)n/(n)!*1/(n+z)
Особые точки n=-z
Г(x)= 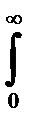e-ttx-1dt
Г(x+1)=xГ(x) Rez>0 Г(z+1)=zГ(z)
Г(z)=Г(z+1)/zRez>-1 z 
0
Г(z+2)=z2Г(z) Rez>-2 z 
0,1
Вопросы к экзамену по математическому анализу
(2 курс, 3 семестр)
1. Свойства сходящихся числовых рядов.
2. Критерий Коши. Необходимое условие сходимости числовых рядов.
3. Признаки сравнения числовых рядов.
4. Признаки Коши и Даламбера.
5. Интегральный признак сходимости.
6. Абсолютная и условная сходимость числовых рядов.
7. Признак Лейбница для знакочередующихся рядов.
8. Признак Дирихле.
9. Переместительное свойство абсолютно сходящихся рядов.
10. Критерий Коши равномерной сходимости функциональных последовательностей.
11. Критерий Коши равномерной сходимости функциональных рядов.
12. Признаки Вейерштрасса и Дирихле.
13. Непрерывность суммы равномерно сходящегося функционального ряда (РСФР).
14. Почленное интегрирование РСФР.
15. Почленное дифференцирование РСФР.
16. Предел последовательности комплексных чисел. Необходимое и достаточное условие.
17. Кривые и области на комплексной плоскости. Основные определения.
18. Предел функции комплексной переменной (ФКП).
19. Непрерывность ФКП.
20. Основные элементарные ФКП.
21. Дифференцирование ФКП. Условие Коши-Римана (теорема).
22. Условия Коши в полярных координатах.
23. Теорема о существовании сопряженной гармонической функции.
24. Геометрический смысл производной гармонической функции.
25. Общие свойства конформных отображений.
26. Круговое свойство дробно-линейной функции.
27. Принцип сохранения симметрии при дробно-линейном отображении.
28. Конформное отображение дробно-линейной функцией:
а) верхней полуплоскости на единичный круг
б) единичного круга на единичный круг.
29. Конформные отображения элементарными функциями (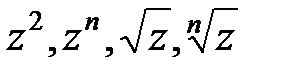 
).
30. Конформные отображения функциями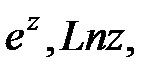 
функцией Жуковского.
31. Интегральная теорема Коши для односвязной области.
32. Аналитичность интеграла с переменным верхним пределом.
33. Интегральная теорема Коши для многосвязной области.
34. Интегральная формула Коши.
35. Теорема о бесконечной дифференцируемости аналитической функции.
36. Теорема Морера.
37. Принцип максимума модуля.
38. Теорема Лиувилля.
39. Основная теорема алгебры.
40. Равномерная сходимость рядов ФКП.
41. Непрерывность суммы равномерно сходящихся рядов ФКП.
42. Почленное интегрирование равномерно сходящихся рядов ФКП.
43. 1 теорема Вейерштрасса.
44. 2 теорема Вейерштрасса.
45. Теорема Абеля.
46. Круг и радиус сходимости степенного ряда.
47. Теорема Тейлора.
48. Теоремы о нулях аналитической функции (теорема об изолированности
нулей аналитической функции и следствие).
49. Теорема Лорана.
50. Неравенство Коши.
51. Классификация изолированных особых точек аналитической функции.
52. Ряд Лорана в окрестности устранимой особой точки.
53. Ряд Лорана в окрестности полюса.
54. Теорема Сохоцкого.
55. Вычисление вычетов аналитической функции.
56. Основная теорема теории вычетов.
57. Вычисление определенных интегралов с помощью теории вычетов.
58. Теорема единственности.
59. Аналитическое продолжение Г-функции.
Лектор Ильинкова Н.И