Круговая диаграмма напряженного состояния

При расчете на прочность деталей, работающих в условиях сложного напряженного состояния, необходимым условием является определение главных напряжений. Однако это не означает, что всегда нужно решать кубическое уравнение, т.к. в большинстве встречающихся на практике случаях одна из площадок является главной, тогда положение двух других главных площадок определяется довольно просто (Рис.9.7).

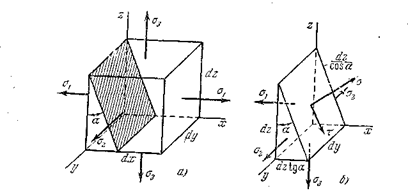
Рис. 9.7

Рассмотрим равновесия прямоугольной призмы, показанной на рис. 9.7. Составим сумму проекций сил на направления 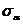и

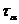
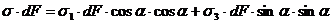
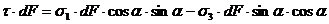
Откуда

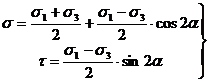(9.10)

Обозначим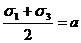

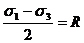
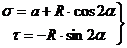(9.10а)

Уравнения (9.10) и (9.10а) в координатах 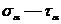представляют собой уравнение окружности в параметрической форме. Роль параметра играет угол 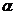. Эту окружность принято называть кругом напряжений Мора (Рис. 9.8).

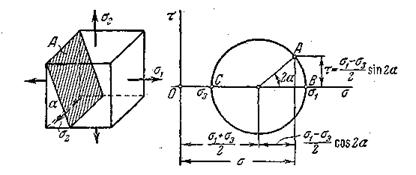
Рис. 9.8

Каждой наклонной площадке, определенной углом 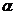(рис. 9.8) на окружности соответствует некоторая точка, которую называют изображающей точкой 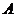. Координаты этой точки .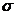

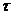Экстремальные касательные напряжения

Прежде всего, укажем, что формулы 9.10 пригодны для плоского напряженного состояния, причем наклонные площадок, параллельны одной из главных осей. Действительно, из рис. 9.9 видно, что 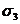не дает проекций на плоскость 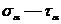. Таким образом формулы 9.10 остаются в силе.

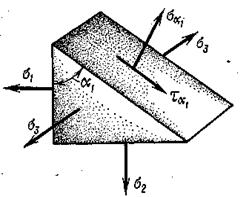
Рис. 9.9

Построим поочередно три круга Мора для семейства площадок параллельных осям 1.2.3 (Рис. 9.10).

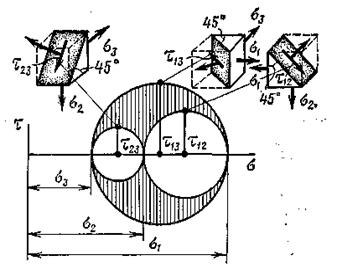
Рис. 9.10

Отмеченные точки являются вершинами кругов, которые соответствуют диагональным площадкам наклонным под углом 45⁰ к главным осям. В теории упругости доказывается, что для произвольно наклонных площадок (не параллельных ни одной из главных осей) нормальное и касательное напряжения определяются координатами точек заштрихованной области.

Как видно из рис. 9.10 максимальные касательные напряжения равны

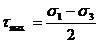(9.11)

Переход тела из упругого состояния в пластическое иногда связывают с величиной 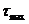, и поэтому наряду с главными напряжениями 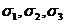оно является важной характеристикой напряженного состояния.

Октаэдрические площадки. Октаэдрические напряжения

Площадка равно наклоненная к главным осям ( 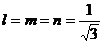), носит название октаэдрической. Напряжения, действующие на ней — октаэдрическими (рис.9.11).

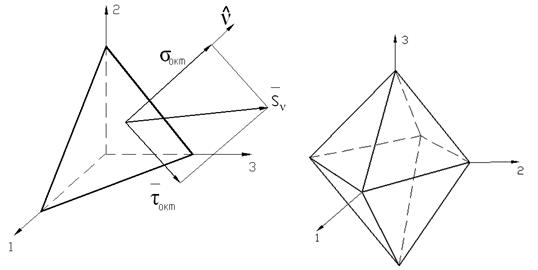
а) б)

Рис. 9.11

Для такой площадки:

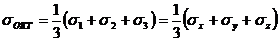(9.12)

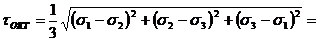
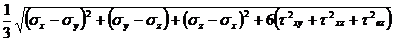(9.13)

Величина

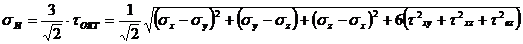(9.14)

носит название интенсивности напряжений.

При изучении вопросов пластичности общая деформация материала в окружности точки разделяется на деформацию изменения объема и формы. С 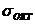связывают изменения объема, а с 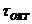изменения формы.

Деформированное состояние

Изменение формы тела связано с перемещением его точек. Расстояние между положением точки до деформации и после деформации 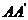называют полным перемещением (Рис. 9.12).

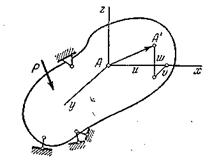
Рис. 9.12

Составляющие вектора полного перемещения по осям обозначим через .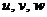

Рассмотрим два ребра параллелепипеда 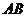и 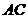. Для простоты на

рис. 9.13 показан отдельно.

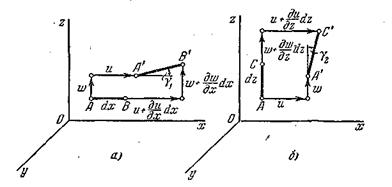
Рис. 9.13

После деформации отрезок 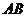занял положение 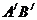. Составляющие вектора перемещений точки 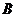отличаются от составляющих вектора перемещений точки 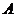на величины, соответствующие координате точки 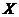. Точка 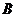переместилась вдоль оси 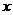на величину 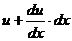, а по оси .

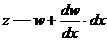Аналогично и с ребром .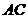

Относительное удлинение ребра 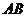по оси x равно

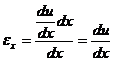по аналогии .

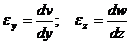Угол поворота 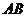в плоскости 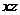равен

.

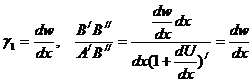Угол поворота отрезка АС в плоскости 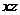равен

.

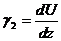Сумма углов 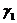и 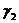представляет собой изменение прямого угла ВАС, т.е. угла сдвига в плоскости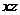

.

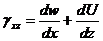Аналогично можно записать выражение углов сдвига и в двух других плоскостях. Окончательно имеем связь между перемещениями и деформациями в точке:

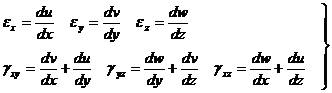(9.15)

Совокупность деформаций, возникающих по различным осям и в различных плоскостях, проходящих через данную точку, носит название деформированного состояния в точке (тензор).

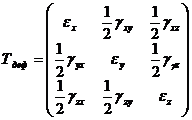(9.16)

Анализ деформированного состояния показывает, что оно обладает свойствами аналогичными свойствам напряженного состояния.

Среди семейства осей, которые могут быть проведены через данную точку, существует три взаимно перпендикулярные оси, в системе которых угловые деформации равны нулю. Эти оси называются главными осями деформаций, а линейные деформации в этой системе — главными деформациями.

Главные деформации определяются из кубического уравнения

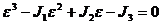, (9.17)

где

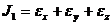
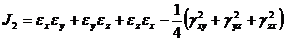
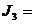
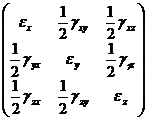
Из сопоставления с напряженным состоянием видно, что аналогом нормального напряжения здесь является линейная деформация, аналогом касательного напряжения половина угла сдвига.

Наряду с линейными и угловыми деформациями в сопротивлении материалов часто определяют объемную деформацию.