Напряжения в брусе при чистом изгибе
Рассмотрим наиболее простой из изгибов — чистый. В этом случае изгибающий момент по длине балки остается постоянным, а перерезывающая сила равна нулю. Так в средней части балки, показано на рис. 5.2, возникает изгиб.
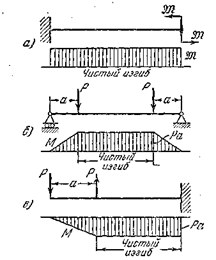
Рис. 5.2
Изучим закон распределения напряжений в поперечном сечении бруса при чистом изгибе.
Будем полагать, что поперечное сечение имеет хотя бы одну ось симметрии и нагрузки приложены в плоскости, проходящей через нее.
Если на боковую поверхность бруса, находящегося в условиях чистого изгиба, нанести ортогональную сетку (рис. 5.3), то линии перпендикулярные к оси бруса 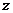 переместятся в плоскости, но останутся прямыми.
переместятся в плоскости, но останутся прямыми.
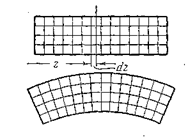
Рис. 5.3
Можно предполагать, что и поперечные сечения плоские до деформации останутся плоскими и после деформации, т.е. справедлива гипотеза плоских сечений Бернулли.
Образование деформаций при чистом изгибе может рассматриваться как результат поворота плоских поперечных сечений друг относительно друга (рис. 5.3). Рассмотрим два смежных сечения, отстоящих один от другого на расстоянии 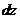 (рис. 5.4).
(рис. 5.4).
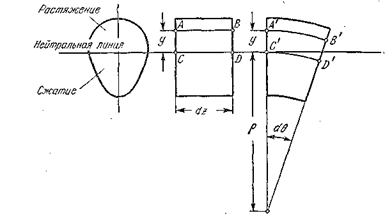
Рис. 5.4
Примем левое сечение условно за неподвижное. Тогда в результате поворота правого сечения на угол 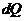 верхние слои удлинятся, а нижние — укоротятся. Очевидно, существует слой, в котором удлинения отсутствуют. Назовем его нейтральным слоем. Отметим его отрезком
верхние слои удлинятся, а нижние — укоротятся. Очевидно, существует слой, в котором удлинения отсутствуют. Назовем его нейтральным слоем. Отметим его отрезком 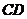 . В результате поворота сечений изменение кривизны нейтрального слоя будет следующим:
. В результате поворота сечений изменение кривизны нейтрального слоя будет следующим:
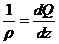 .
.
Произвольно взятый отрезок 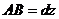 (рис. 5.4) получим приращение длины
(рис. 5.4) получим приращение длины 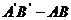 . Так как сечения остаются плоскими,
. Так как сечения остаются плоскими,
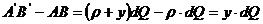 ,
,
где 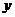 — расстояние от рассматриваемого отрезка
— расстояние от рассматриваемого отрезка 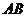 до нейтрального слоя
до нейтрального слоя 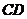 . Положение этого слоя пока неизвестно.
. Положение этого слоя пока неизвестно.
Относительное удлинение слоя 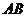 равно
равно
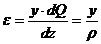 . (5.4)
. (5.4)
Если предположить, что продольные волокна бруса не давят друг на друга, то каждое из них находится в условиях простого растяжения или сжатия.
В этом случае справедлив закон Гука
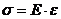 .
.
Подставляя 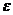 из предыдущей формулы, имеем
из предыдущей формулы, имеем
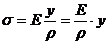 . (5.5)
. (5.5)
Таким образом, при чистом изгибе напряжения меняются в поперечном сечении по линейному закону.
Геометрическое место точек в сечении удовлетворяющее условию 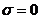 , называется нейтральной линией сечения. Нейтральная линия очевидно перпендикулярна к плоскости кривизны изогнутого бруса.
, называется нейтральной линией сечения. Нейтральная линия очевидно перпендикулярна к плоскости кривизны изогнутого бруса.
Свяжем теперь напряжения 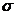 с внутренними силовыми факторами, возникающими при чистом изгибе.
с внутренними силовыми факторами, возникающими при чистом изгибе.
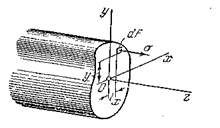
Рис. 5.5
Сумма элементарных сил 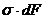 (рис.5.5) дает нормальную силу
(рис.5.5) дает нормальную силу 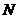 в сечении. Но при чистом изгибе
в сечении. Но при чистом изгибе 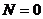 , поэтому
, поэтому 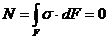 или после подстановки
или после подстановки 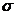 имеем
имеем 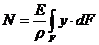 . Откуда
. Откуда 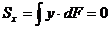 — статический момент площади относительно нейтральной оси. Так как статический момент площади равен нулю, то нейтральная линия проходит через центр тяжести сечения.
— статический момент площади относительно нейтральной оси. Так как статический момент площади равен нулю, то нейтральная линия проходит через центр тяжести сечения.
Теперь система координат 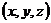 может быть конкретизирована. Начало координат поместим в центр тяжести сечения. Ось
может быть конкретизирована. Начало координат поместим в центр тяжести сечения. Ось 
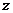 направим по нормали к сечению. Ось
направим по нормали к сечению. Ось 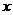 по нейтральной линии. Ось
по нейтральной линии. Ось 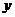 будет лежать в плоскости изменения кривизны.
будет лежать в плоскости изменения кривизны.
Пока мы рассматривали плоский изгиб, когда плоскость момента и кривизны совпадают.
При указанном случае момент элементарных сил 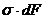 относительно оси
относительно оси 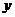 равен нулю, а относительно оси
равен нулю, а относительно оси 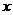 полному изгибающему моменту
полному изгибающему моменту 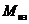 .
.
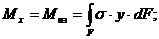
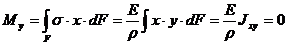 (5.6)
(5.6)
Второе выражение приводится к виду 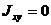 . Оно равно нулю в том случае, если плоскость изгибающего момента проходит через одну из главных осей. Такой изгиб называется плоским (прямым).
. Оно равно нулю в том случае, если плоскость изгибающего момента проходит через одну из главных осей. Такой изгиб называется плоским (прямым).
Из выражения (5.6) получаем зависимость кривизны бруса от изгибающего момента:
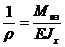 (5.7)
(5.7)
Возвращаясь к формуле (5.5) и, исключая из нее кривизну 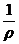 , получаем выражение для напряжения
, получаем выражение для напряжения 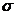 :
:
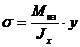 (5.8)
(5.8)
Максимальные напряжения при изгибе возникают в точках наиболее удаленных от нейтральной линии (рис. 5.6).
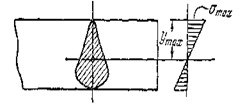
Рис. 5.6
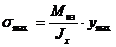 ; отношение
; отношение 
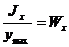 называется моментом сопротивления сечения. Таким образом,
называется моментом сопротивления сечения. Таким образом,
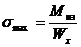 (5.9)
(5.9)
Используя последнее выражение можно записать условие прочности при изгибе
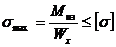 5.10)
5.10)
Моменты сопротивления простейших сечений:
— для прямоугольного сечения со сторонами 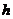 и
и 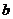
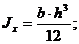
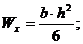
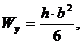
— для круглого сечения
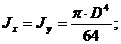
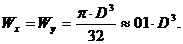
Таким образом, напряжения при изгибе обратно пропорциональны третьей степени линейных размеров сечения.
Наиболее экономичными являются сечения, для которых с наименьшей затратой материала получается наибольшая величина момента сопротивления 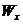 .
.
Для рационально работающей на изгиб балки необходимо, по возможности, распределить площадь подальше от нейтральной оси. Так возникли стандартные двутавровые и швеллерные тонкостенные профили, показанные на ри.5.7.
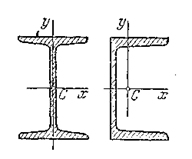
Рис. 5.7
