Частные случаи приведения пространственной системы сил

№	Значения главного вектора и главного момента	Результат приведения
		Система сил приводится к паре сил, момент которой равен главному моменту (главный момент системы сил не зависит от выбора центра приведения О).
		Система сил приводится к равнодействующей, равной , проходящей через центр О.
		Система сил приводится к равнодействующей , равной главному вектору и параллельной ему и отстоит от него на расстоянии . Положение линии действия равнодействующей должно быть таким, чтобы направление ее момента относительно центра приведения О совпадало с направлением относительно центра О.
	, причем векторы и не перпендикулярны	Система сил приводится к динаме (силовому винту) – совокупности силы и пары сил, лежащей в плоскости, перпендикулярной к этой силе.
		Система сил, приложенных к твердому телу, является уравновешивающейся.

30. Приведение к динаме. Динамой в механике называют такую совокупность силы и пары сил ( ) действующих на твердое тело, у которой сила перпендикулярна плоскости действия пары сил. Используя векторный момент пары сил , можно также определить динаму как совокупность силы и пары, у которы сила параллельна векторному моменту пары сил.

Уравнение центральной винтовой осиПредположим, что в центре приведения, принятом за начало координат, получены главный вектор с проекциями на оси координат и главный момент с проекциями При приведении системы сил к центру приведения О₁ (рис. 30) получается динама с главным вектором и главным моментом , Векторы и как образующие линаму. параллельны и поэтому могут отличаться только скалярным множителем k_0. Имеем,, так как .Главные моменты и , удовлетворяют соотношению

Подставляя , получим

Координаты точки О₁ в которой получена динама, обозначим х, у, z. Тогда проекции вектора на оси координат равны координатам х, у, z. Учитывая это, (*) можно выразить в форме

где i. j ,k - единичные векторы осей координат, а векторное произведение * представлено определителем. Векторное уравнение (**) эквивалентно трем скалярным, которые после отбрасывания можно представить в виде

Полученные линейные уравнения для координат х, у, z являются уравнениями прямой линии - центральной винтовой оси. Следовательно, существует прямая, в точках которой система сил приводится к динаме.

31 Условия и уровнения пространственной системы сил

Для равновесия пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент этой системы равнялись нулю. Достаточность: при F_o=0 система сходящихся сил, приложенных в центре при­ведения О, эквивалентна нулю, а при М_о=0 система пар сил эквивалентна нулю. Следовательно, исходная система сил эквива­лентна нулю. Необходимость: Пусть данная система сил эквивалентна нулю. Приведя систему к двум силам, заметим, что система сил Q и Р (рис. 4.4) должна быть эк­вивалентна нулю, следовательно, эти две силы должны иметь общую линию действия и должно выполняться рав-во Q=–Р. Но это может быть, если линия действия силы Р проходит через точку О, т. е. если h=0. А это значит, что главный момент равен нулю (М_о=0). Т.к. Q+Р=0, a Q=F_o+P', то F_o+P'+P=0, и, следовательно, F_o = 0. Необх и достуслравновпро­странственнойсист сил им вид: F_o=0, M_o=0 (4.15),

или, в проекциях на координатные оси, Fox=åF_kx=F_1x+F_2x+…+F_nx=0; F_Oy=åF_ky=F_1y+F_2y+...+F_ny=0; F_oz=åF_kz=F_1z+F_2z+…+F_nz=0 (4.16). M_Ox=åM_Ox(F_k)=M_Ox(F₁)+М_ox(F₂)+...+M_Ox(F_n)=0, M_Oy=åM_Oy(F_k)=M_oy(F₁)+M_oy(F₂)+…+M_oy(F_n)=0, М_oz=åМ_Оz(F_k)=М_Оz(F₁)+M_oz (F₂)+...+М_oz(F_n)=0. (4.17)

Т.о. при решении задач имея 6 ур-ий можно найти 6 неизвестных. Замечание: пару сил нельзя привести к равнодействующей. Частные случаи: 1) Равновесие пространственной системы параллельных сил. Пусть ось Z параллельна линиям действ силы (рис 4.6), тогда проекции сил на x и y равны 0 (F_kx=0 и F_ky=0), а остаётся только F_oz. А что касается моментов, то остаются только M_ox и M_oy, а M_ozотсутствует. 2) Равновесие плоской системы сил. Остаются ур-я F_ox, F_oy и момент M_oz (рис 4.7). 3) Равновесие плоской системы параллельных сил. (рис. 4.8). Остаются только 2 ур-я: F_oy и M_oz.При составлении ур-ий равновесия за центр привидения может быть выбрана любая точка.

Если система сил находится в равновесии, то ее главный вектор и главный момент равны нулю:

Эти векторные равенства приводят к следующим шести скалярным равенствам:

которые называются условиями равновесия пространственной произвольной системы сил.

32 теорема Вариньона, согласно которой моментравнодействующей системы сил относительно какого-либо центра равен геометрической сумме моментов составляющих систему сил относительно того же центра.

Рисунок 1.17

Например, момент силы F относительно точки O можно определить как алгебраическую сумму моментов сил F_x и F_y (на которые можно разложить силу F ) относительно той же точки O (рисунок 1.17). То есть

M_o(F)= -Fh = -F_x y+ F_y x, (1.8)

где F_x , F_y , x и y – проекции на оси координат силы F и радиуса-вектора r .

Центр параллельных сил

Рассмотрим систему параллельных сил {F1, F2, ..., Fn}. При повороте всех сил системы на один и тот же угол линия действия равнодействующей системы параллельных сил повернется в ту же сторону на тот же угол вокруг некоторой точки (рисунок 1.5, а).   Эта точка называется центром параллельных сил.   Согласно теореме Вариньона, если система сил имеет равнодействующую, то ее момент относительно любого центра (оси) равен сумме моментов всех сил системы относительно того же центра (оси). 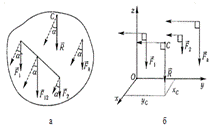  Рисунок 1.5   Для определения координат центра параллельных сил воспользуемся этой теоремой. Относительно оси x Mx(R) = ΣMx(Fk), - yCR= ΣykFk и yC = ΣykFk /ΣFk. Относительно оси y My(R) = ΣMy(Fk), - xCR = ΣxkFk и xC = ΣxkFk /ΣFk. Чтобы определить координату zC, повернем все силы на 90° так, чтобы они стали параллельны оси y (рисунок 1.5, б). Тогда Mz(R) = ΣMz(Fk), - zCR = ΣzkFk и zC = ΣzkFk /ΣFk. Следовательно, формула для определения радиус-вектора центра параллельных сил принимает вид rC = ΣrkFk /ΣFk. Свойства центра параллельных сил:   1 Сумма моментов всех сил Fk относительно точки C равна нулю ΣMC(Fk) = 0. 2 Если все силы повернуть на некоторый угол α, не меняя точек приложения сил, то центр новой системы параллельных сил будет той же точкой C.

34 Центром тяжести твердого тела называется геометрическая точка, жестко связанная с этим телом, и являющаяся центром параллельных сил тяжести, приложенных к отдельным элементарным частицам тела (рисунок 1.6).

Радиус-вектор этой точки

Рисунок 1.6

Для однородного тела положение центра тяжести тела не зависит от материала, а определяется геометрической формой тела.

Если удельный вес однородного тела γ, вес элементарной частицы тела

P_{k =} γΔV_k (P ₌ γV) подставить в формулу для определения r_C, имеем

Откуда, проецируя на оси и переходя к пределу, получаем координаты центра тяжести однородного объема

Аналогично для координат центра тяжести однородной поверхности площадью S (рисунок 1.7, а)

Рисунок 1.7

Для координат центра тяжести однородной линии длиной L (рисунок 1.7, б)

35На каждую частицу тела, находящегося вблизи поверхности Земли, действуетнаправленная вертикально вниз сила, которая называется силой тяжести. Силы тяжести каждой частицы тела, строго говоря, направлены по радиусам к центру Земли и не являются параллельными. Но для тел, размеры которых малы по сравнению с размерами Земли, непараллельность настолько незначительна, что в расчетах с большой точностью силы тяжести их частиц можно считать параллельными, сохраняющими свои значения, точки приложения и параллельность при любых поворотах тела. Поэтому, обозначив силу тяжести частицы через Рк , можно, согласно

формулам и , найти точку С, которая неизменно связана с телом и называется центром системы параллельных сил тяжести. Таким образом, центром тяжести твердого тела называется центр системы параллельных сил тяжести частиц данного тела. Точка С — это геометрическая точка, она может и не принадлежать телу, но она всегда с ним связана, например центр тяжести баскетбольного мяча, кольца и др. Выразим силу тяжести (вес) частицы тела через ее объем V. Тогда величина называется удельным весом, а величина - плотностью тела в данной точке. ("гамма"-Н/м3) ("ро"-Н*с2/м4)