Простое алгебраическое расширение как линейное пространство.

О1)Комплексное число называется алгебраическим если оно является корнем не нулевого многочлена с рациональными коэффициентами и называется трансцендентным в противном случае.

Например алгебраическими являются

1)корни многочленов 1 степени x=a/b

2) числа вида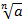

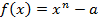
3)

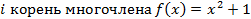
4) 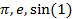не являются.

Аналогично можно определить понятие алгебраических и трансцендентных чисел.

О2) Число a называется алгебраическим относительно поля p если оно является корнем некоторого многочлена f(x) с коэффициентами из этого поля p и трансцендентным в противном случае.

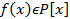
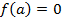
Очевидно если a является алгебраическим относительно p то оно является алгебраическим для любого поля В которое содержит p в качестве подполя.

Например число 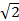алгибраическое атностильно Q по этом будет алгебраическим относительно С.

Каждое алгебраическое число является корнем многих многочленов с рациональными коэффициентами.

О3) нормированный многочлен f(x) не приводимый над полем D который имеет число a своим корнем называется минимальным многочленом числа a. А степень многочлена называется степенью Алгебраического числа a относительно поля D.

Если число a является корнем многочлена 1 степени а сам многочлен 1 степени не приводим не над каким полем. То a принадлежит D, если число a является корнем не приводимого над D многочлена f(x) степени > 1 то a не принадлежит D та как в противном случае еслиa он должно быть простым, что противоречит условию другими словами a алгебраическое относительно D самому полю не принадлежит.

Пусть a алгебраическое число относительно D и оно полю не принадлежит рассмотрим минимальное поле которое содержит в себе поле D и число a. Обозначим его D(a) такое минимальное поле называют простым алгебраическим расширением.

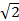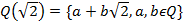Пусть дано алгебраическое число Q=Δ , . Если поле получено из поля Δ присоединением к нему конечного числа элементов то такое поле называется составным алгебраическим дополнением, Δ(A,B,C).

Т1:Простое алгебраическое расширение образованное из поля D присоединением алгебраического числа являющегося корнем не приводимого над полем D нормированного многочлена 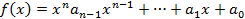(1) состоит из чисел вида

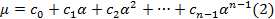
Где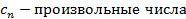

Доказательство:

Покажем, что множество чисел вида (2) содержит в себе поле D и число 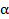. Действительно множество чисел (2) содержет в себе поле D

Положив все 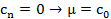которое может принять любое(все) значение из поля D.

Число 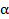также является числом вида (2) так как положив 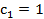а остальные 0 получим, что 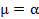. Покажем, что расширение тоже поле.(для этого проверим замкнутость этого множества относительно сложения и умножения и 9 аксиом поля).

Сумма любых (2) чисел вида (2) очевидна даст число того же вида. Покажем, что произведение 2 чисел вида (2) даст число вида (2) для этого представим 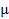как вырожение полученное в результате подстаноки 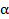в многочлен в место x.

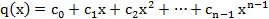
Возьмём 2 числа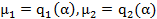

Найдем их произведение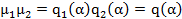

Если ст 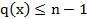, то 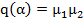- число вида (2).

Если ст 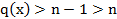то поделим с остатком многочлен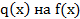

То есть наш многочлен равен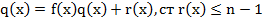

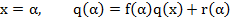
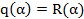
И в этом случае 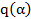являеся числом вида (2)

Покажем выполнение 9 аксиом поля .

Посмотрим на числа вида 2 как на значения многочленов вида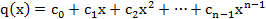

Где 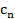–произвольные элементы поля D, и по этому выполняются аксиомы с 1 по 6.

7)Роль 1 на множестве чисел вида (2) будет играть число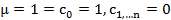

9)Коммутативность умножения следует из того, что при унижение чисел вида (2) получаем число того же вида при чем операция умножения выполняется над коэффициентами которые являются элементами поля следовательно умножение коммутативно.

8) Покажем, что для любого числа найдется обратное того же вида то есть покажем что при делении единице 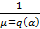будет тем же самым числом. Рассмотрим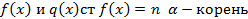

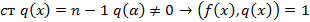
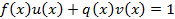
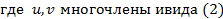
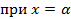
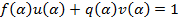
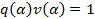
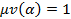
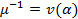
Показали, что числа вида (2) являются полем. Покажем, что это поле минимальное.

Обозначим полученное поле 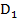покажем, что оно минимальное. C одной стороны простое алгебраическое поле. 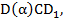с друго сторны 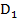состоит из чисел вида (2) 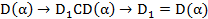таким образом простое алгебраическое расширение является минимальным полем состоящим из поля D и .

■

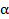Следствие: Если 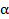корень многочлена 2 степени не приводимого над полем D то простое алгебраическое расширение состоит из чисел вида r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 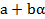где 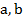элементы поля.И такое расширение называется квадратичным.

Пример 1:

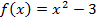этот многочлен не приводим над Q его корни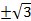

Построим алгебраическое расширение .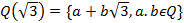

Пример 2:

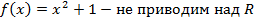
Корни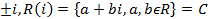

Замечание: В теореме была установлена структура элементов простого алгебраического расширения, это числа вида (2). Числа такого вида содержат произведения 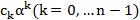, 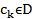такие произведения складываются а сами получены в результате умножения 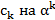.Таким образом число вида (2) представляют линейную комбинацию элементов 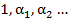скофициентами из поля D то есть на простое алгебраическое расширение можно смотреть как на линейное пространство над D. Роль базиса играют элементы 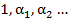.Можно доказать их линейную зависимость (в том, что мы нашли многочлен p степень которого меньше чем f, что противоречит, что f наименьшей степени).