Отыскание рациональных корней многочлена

Т1: Если рациональное число является корнем многочлена f(x) то свободный член делится на p а старший коэффициент делится на q.

Доказательство:

t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>=0 </m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 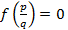по условию. Обе части этого выражения умножим на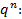

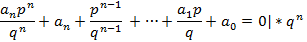
/…СБ4/

2 часть доказательства

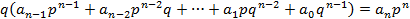
Левая часть делится на q 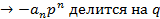g w:val="EN-US"/></w:rPr><m:t>q</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> .

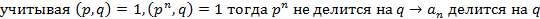Если старший член равен 1 (нормированный) то все рациональные корни этого многочлена являются целыми числами причем делителями свободного член

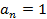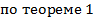
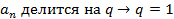, , , cследовательно корень целый.

Т2:Если рациональное число где p,q взаимно простые является

корнем многочлена f(x) то для любого целого числа k:

применима теорему о делении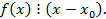

Доказательство:

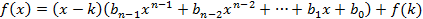
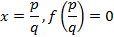
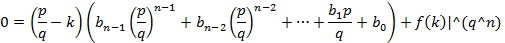
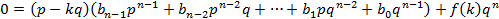
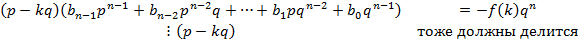
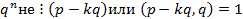
Если предположить, что (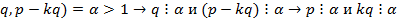

Получаем, что наша дробь сократима, что противоречит нашему условию. Мы пришли к тому, что 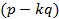делится не может следовательно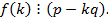

■

Следствие: Если многочлен с целыми коэффициентами нормированный то его рациональными корнями могут быть только такие целые числа для которых при любом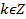

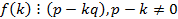
Доказательство:

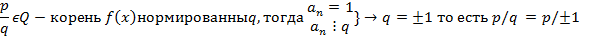
По Т2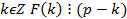

30 Т(Критерий не приводимости Эйзенштейна):

Если в многочлене с целыми коэффициентами f(x) коэффициенты все до старшего делятся на некоторое простое число p и старший коэффициент не делится на p причем 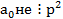, то такой многочлен не приводим над полем рациональных чисел Q.

Доказательство:

Пусть эти требования выполняются но многочлен является приводимым то есть представляется в виде произведения:

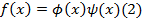
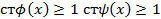
пусть

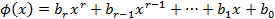
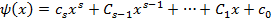
Подставим выражения для 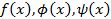в равенство(2).

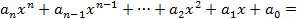
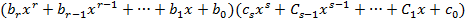
Выполним почвенное умножение в правой части равенства, приведем подобные слагаемые и воспользуемся определением равных многочленов то есть мы приравняем соответствующие коэффициенты:

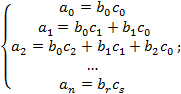
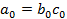По условию теоремы Учитывая, что , то 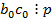, тогда либо 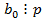или либо . По условию 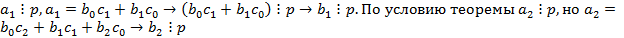. Продолжая так и далее получим, что 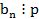от куда следует, что , что противоречит условию, что и доказывает нашу теорему. Заметим, что рассматривая второй случай также пришли к противоречию. В этом случае было бы получено, что 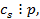что значит и 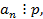что противоречит теореме.

■

Замечание: Из теоремы следует существование многочленов сколь угодно большой степени с целыми коэффициентами не приводимыми над полем Q. Например 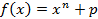является не приводимым над Q.

Пример 1:

Доказать не приводимость многочленов пользуясь критерием Эйзенштейна:

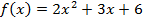
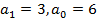
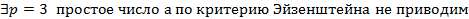
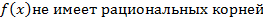
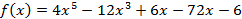
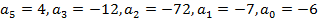
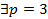
На полем Q не приводим.

Алгебраические числа.