Л1 02.09.09 Алгебра многочленов

Л1 02.09.09 Алгебра многочленов

Лит: Винбег Алгебра многочленов

Задачник практикум

Т1: Многочлены от одной переменной

Многочлены как функции действительной переменной

Рассмотри понятия многочлена или целой рациональной функции от одной переменной.

О1) функция вида:

(1) –называется многочленом

Где действительные числа, x действительная переменная, n целое число- степень многочлена.

коэффициенты, Число n называют степенью многочлена, – свободный член.

С точке зрения мат записи имеем сумму например:

- 1 степени;

-2 степени;

Частным случаем является постоянная функция f(x)=a ,a-cost.

Многочлен коэффициенты которого равны 0 называется, многочлен нулевой степени.

Заметим что над многочленами можно выполнять: сложение, вычитание, умножения в результате чего получается снова многочлен. Пусть имеется многочлен (1) и многочлен: ;(2)

тогда:

;

Произведением многочленов f и g называется сумме всевозможных произведений U*V где U любой член из f(x), а V из g(x) тогда:

;

где:

Так как сумма, разность и произведение многочленов также являются многочленом то многочлены образуют под кольцо в кольце всех функций действительного аргумента. Кольцо многочленов от действительной переменной x обозначается R[x] . Поскольку кольцо всех функций коммутативно и ассоциативно кольцо R[x] также обладает этими свойствами а значит в нем существует единичный элемент f(x)=1. Многочлены в алгебре также в связи с решением уравнений f(x)=0 где левая часть многочлен n-ной степени от одной переменной то в этом случае многочлен рассматривается как многочлен комплексной переменно. В алгебре рассматривают многочлены на более общих алгебраических системах, коэффициенты которых принадлежат произвольному кольцу, значительно отличаются от многочленов с числовыми коэффициентами.

Алгебраическое определение кольца многочленов

О1) Пусть R[x] произвольное кольцо многочленов от переменной х с коэффициентами из R назовем формальное выражение:

(1)

где n целое число выражение (1) надо рассматривать как единый символ у которого операции над отдельными частями не подразумевается будем называть коэффициентами многочлена (1) при , а для всех k>n коэффициент при равен 0 для обозначения многочлена используют .

Два многочлена будем считать равными если каждый коэффициент из равен соответствующему коэффициенту из и записывается f(x)=g(x).

Для многочленов (1) и(2) определим их сумму f(x)+g(x) и произведение f(x)*g(x) по формулам рассмотренным в §1. Эти определения согласуются с данным выше определением равенства многочленов:

f1(x)=f2(x);

g1(x)=g2(x);

f1(x)+g1(x)=f2(x)+g2(x);

f1(x)*g1(x)=f2(x)*g2(x);

Деление с остатком

Между кольцом многочленов от одной переменной и кольцом целых чисел имеется глубокая аналогия проявляющаяся в свойствах делимости, в разложении на простые множества причина аналоги состоит в том что, в обоих этих кольца выполнимо деление с остатком благодаря чему оба эти кольца являются евклидовыми.

Т(Делении с остатком): Пусть P произвольное поле, P[x] кольцо многочленов с коэффициентами из P возьмем f(x) и g(x)≠0 тогда существует единственная пара многочлена q(x),r(x) ∈P[x] удовлетворяющая условиям:

1)f(x)=g(x)q(x)+z(x)

2)ст z(x)<ст g(x).

Доказательство:

Пусть:

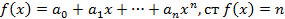
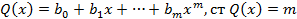
Если n<m то не полное частное равно 0 а, остаток совпадет с самим многочленом f(x).

Рассмотри когда n≥m. Построим многочлен ,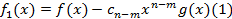

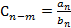
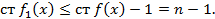Обозначим .

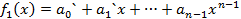Аналогично построим 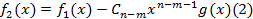. Где , .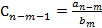

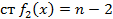Продолжая процесс построения многочленов будет получена конечная последовательность многочленов и последний многочлен будет иметь номер n-m+1 и имеет степень 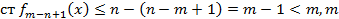-степень многочлена g(x). Последний многочлен: 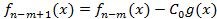. Почвенное сложение равенств (1) (2) и т.д. дает возможность выразить многочлен f(x) через g(x):

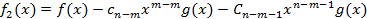
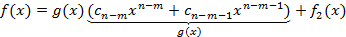
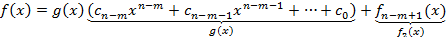
То есть наш многочлен представим в виде:

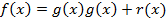
Докажем единственность такова представления методом от противного.

Предположим что, существуют такие многочлены 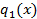и 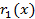что, выполняется: 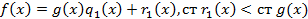тогда:

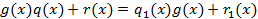
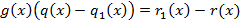
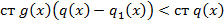
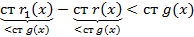
Учитывая что, степень левой части больше или равна а, степень правой ее не превосходит получили противоречие из которого следует: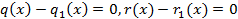

Рассмотренная процедура деления с остатком лежит в основе отыскания наибольшего делителя 2 многочленов.

Кратные корни многочлена

О) Элемент называется корнем k-ой кратности для многочлена если но не делится .

Пример 1:

x=2 - корень 2 кратности.

Т1: Чтобы элемент был корнем k-ой кратности необходимо и достаточно, что бы выполнялось условие (1)

Доказательство:

⟹ Пусть корень k-ой кратности для многочлена тогда по определению будим иметь то есть где , учитывая, что в разложении f(x) он входит в k степени то в его производную он войдет в k-1 степени:

где причем . Аналогично по теореме предыдущего параграфа не приводимый множитель ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> войдет в k-2 степени.

, где причем действуя так далее находим причем

не , т.е. .

⟸ Пусть выполнены требования 1 то есть корень многочлена f(x) пусть кратность этого корня равна и она отличается от k:

1) <k è -1<k-1 è учитывая, что ≤k-1 (по доказанной первой части теоремы полученные соотношения противоречивы.

2) >k по первой части доказанной теоремы получится:

получили противоречивые соотношения таким образом .

■

§14 разложение многочлена по степеням двучлена

Пусть дан многочлен f(x) ∈P[x] с нулевой характеристикой и степень его равна n.

Поставим задачу разложить f (x) по степеням где то есть представим многочлен f(x) в виде где подлежат отысканию. Многочлен в виде (1) продифференцируем n раз:

Подставляя в полученные неравенства :

Подставим найденные коэффициенты в (1) получим:

Коэффициенты в (2) определяются однозначно.

Пример 1:

разложить по степеням .

Найдем коэффициенты для проверки при помощи схемы Горнера   -3 -2 55= 91   51   12   1

Пример 2:

Найти интеграл:

-4

Т2: Многочлены от нескольких переменных.

Cсимметрические многочлены

Будим рассматривать многочлены над произвольной областью целостности.

О1 называется симметрическим если он не меняется при любой перестановке входящих в него переменных где –перестановка

Пример 1:

– симметрический

- не симметрический

Структура симметрических многочленов такова, что если сам симметрический многочлен содержит элемент , то он также должен содержать многочлен вида у которых выполнена замена иксов, а индексы образуют перестановку из номеров переменных x. Обозначим сумм различных одночленов, которые получаются из одночлена , . В частности каждый симметрический многочлен является суммой однородных многочленов

Особую роль среди симметрических многочленов играют элементарные симметрические многочлены.

По определению k-ый элементарный симметрический многочлен есть сумм всевозможных произведений по k различных переменных

Другую важную серию симметрических многочленов составляют степенные суммы:

Можно показать что, сумма разность и произведение симметрических многочленов также являются симметрическими

Пример 2:

–симметрические их произведение надо показать что он тоже симметрический

è - симметрический.

K из него можем выделить симметрические. Сами симметрический многочлен тоже образуют кольцо.

Рассмотрим ряд утверждений относительно симметрически многочленов.

Л1: Если лексико старший член симметрического многочлена то для последовательности степеней выполняется .

Доказательство:

Пусть u лексикографически старший член. Предположим . По условию f симметрический тогда по определению симметрического многочлена он в месте с одночленом U содержит одночлен . Исходя из предположения но по условию U старший то есть наше предположение привело к противоречию условию леммы следовательно наше предположение не верно.

Л2: Для любого одночлена где , a≠0 суш шествует многочлен лексикографически старшй член которого совподает c U.

Доказательство:

Лексикографически старший член многочлена является произведением старших членов элементарных симметричных многочленов с учетом их степеней:

Найденный лексикографически старший член должен быть равен одночлену U если

(2)

Решение системы (2) получаем в результате вычитания из i-го уравнения i+1 уравнение:

(3)

Такое решение единственно и учитывая что, , - целые не отрицательные числа а, следовательно могут быть показателями степеней. И так симметрический многочлен:

и лексикографически старший член ее совпадает с U(он единственен, что идет из единственности решения системы 2).

Доказанные леммы 1,2 позволяют рассмотреть основную теорему о симметрических многочленов.

Теорема единственности

Л: пусть

Если старшие члены U и V пропорциональны то соответствующие показатели степеней

.

Доказательство:

Пусть лексикографически старший член U имеет вид ,тогда по Л2 4 . Так как многочлен V ассоциирован с U то их старшие члены отличаются только числовыми коэффициентами …, (на основании Т2 ), из (1),(2) ⟹ …. .

■

Т(Единственность): Всякий симметрический многочлен единственным образом представляется в виде многочлена от элементарных симметрических многочленов.

Доказательство:

Пусть для многочлена существует 2 различных многочлена

f =F

f =G

F≠G

Рассмотрим многочлен H =F -G H ≠0

Пусть все члены многочлена H. Где t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>u</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>s</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> -старшие члены соответственно, среди них ассоциированных не будет(на основании Л3). Выберем из t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>u</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>s</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> лексикографически старший пусть например им будет . После приведения подобных членов в сумме если сохранится то эта сумма равна нулю быть не может, таким образом c одной стороны H равен 0 а, с другой стороны не равен, пришли к противоречию.

■

Дополнение к теме НОД). Результант 2 многочленов

Алгоритм Евклида позволяет найти НОД и НОК двух многочленов и в частности выяснить являются ли они взаимно простыми. Однако в явном виде алгоритм Евклида не дает условия которому должны удовлетворять коэффициенты 2 многочленов чтобы они были(не были) взаимно простыми. Поставим задачу найти соотношение между коэффициентами 2 многочленов выполнение которого было необходимо и достаточно, что бы многочлены не были взаимно простыми.

Пусть

Найдем

Если они взаимно простыми то их НОД= 1и . Если они не взаимно просты то НОД≠ 1 и ст[f,g]<ст fg. Введем обозначения h(x)=[f,g] тогда

f g не являются взаимно простыми → существуют многочлен что, . Выясним когда такие многочлены существуют. Запишем многочлены:

Подставим многочлены в равенство получим:

s w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">

На основании определения равенства многочленов приравниваем их соответствующие коэффициенты(таких равенств будет m+n).

Эта система имеет не нулевое решение если определитель равен 0. Для удобства умножим на -1 и транспонируем и его. Этот определитель называют результантом 2 многочленов.

Т1: Многочлены f,g не являются взаимно простыми когда их результант равен 0.

Результант 2 многочленов может быть применен не только для установления взаимной простоты многочленов но и для решения других задач например для исключения переменной из системы 2 алгебраических уравнений с 2 неизвестными.

О) Системой из m алгебраических уровней с n переменными называется система:

О) Системой 2 алгебраических уравнений с 2 неизвестными называют:

Запишем систему (2) в развернутом виде представив f и как многочлены от одной переменной x из кольца P[y]

Положив получим что, левые части уравнений будут обычными многочленами одной переменной х с коэффициентами из поля P эти многочлены не будут взаимно простыми то есть они будут иметь общие корни а, следовательно и система будит иметь решение если их результант =0:

Подставив в (2’), получаем решение и общее решение такие, что при их подстановке наши 2 уравнения системы (2) обращаются в 0. Применение результанта позволило исключит одну неизвестную.

Пример 1:

Исключить переменную x и найти решение:

Т3:Многочлены над полем комплексных чисел. Уравнения 3 и 4 степени.

Алгебраические числа.

Л1 02.09.09 Алгебра многочленов

Лит: Винбег Алгебра многочленов

Задачник практикум

Т1: Многочлены от одной переменной