Графическое представление статистических распределений выборок

Для получения наглядного представления о распределении выборок строят соответствующие графики, в частности, полигон частот или гистограмму распределения.

Вариационный ряд часто изображают графически в виде полигона частотили полигона относительных частот.

Для построения полигона частот на оси абсцисс откладывают варианты х_i, а на оси ординат – соответствующие им частоты m_i. Точки (х_i; m_i) соединяют отрезками прямых. Полигоном частотназывают ломаную линию, отрезки которой соединяют точки (х₁;m₁);
(х₂; m₂)…..(х_к; m_к).

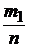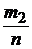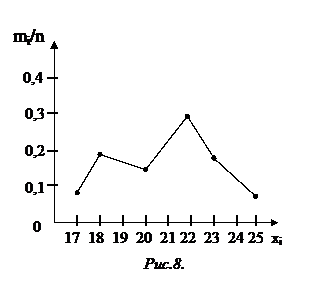
Полигоном относительных частот называют ломаную линию, отрезки которой соединяют точки (х₁; );(х₂; ); (х_к; 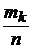). На рис. 8 показан полигон относительных частот, построенный по данным табл.2.

Для непрерывной случайной величины обычно строят гистограммы частотилиотносительных частот.

Гистограммой частот называют диаграмму, состоящую из вертикальных прямоугольников, основаниями которых являются интервалы длиной D х =h, а высоты равны отношению 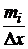(плотности частоты). Для построения гистограммы частот на оси абсцисс откладывают интервалы значений исследуемого показателя (интервалы вариант) и на них строят прямоугольники высотой 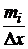. Площадь i -го прямоугольника равна Dх × 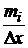= m_i, т.е. равнаколичеству вариант в i-м интервале. Следовательно, площадь гистограммы частот равна сумме частот для всех интервалов, иначе говоря, равна объемувыборки.

Гистограмма относительных частот отличается от предыдущей гистограммы тем, что на ней высоты прямоугольников равны отношению 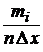,т.е. равны плотности относительной частоты (эмпирической плотности вероятности). В этом случае площадь i-го прямоугольника равнаDх × 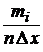= р_i^* – относительной частоте вариант, попавших в i-ый интервал. Напомним, что р_i^* – оценка вероятности попадания значений Х в выбранный интервал. Площадь гистограммы относительных частот равна сумме относительных частот для всех интервалов, т.е. равна единице.

Рис. 9

Гистограмма относительных частот, построенная по данным табл.4, приведена на рис. 9. Из этого рисунка следует, что для используемой выборки интервал наиболее вероятных масс тела новорожденных (3,38 - 3,55) кг.

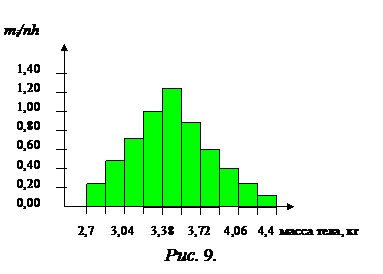Необходимо отметить, что гистограммой называют и серию прямоугольников, высотами которых являются непосредственно частоты m_i для соответствующих интервалов, или относительные частоты (в нормированной гистограмме), а также относительные частоты в процентах (процентная гистограмма). Два последние варианта позволяют сравнивать гистограммы, построенные на одних и тех же интервалах, но для различных выборок из той же генеральной совокупности.

Важно, что гистограммы можно использовать для оценкизакона распределенияпризнака в генеральной совокупности (в популяции). Соединяя средние точки верхних оснований прямоугольников гистограммы относительных частот плавной линией, можно по данным выборки получить примерный вид графика зависимости плотности вероятности f от х. Такая зависимость отражена на рис. 9. Можно предположить, что анализируемый показатель (масса тела новорожденного) в генеральной совокупности распределен по нормальному закону, т.е. нормальный закон является вероятностной моделью для данного признака популяции.