Основные числовые характеристики случайных величин

Результаты, изложенные в параграфах 2.2 и 2.3, показывают, что полную характеристикудискретной и непрерывной случайных величин можно получить, зная законы их распределения. Однако во многих практически значимых ситуациях пользуются так называемымичисловыми характеристиками случайных величин, главное назначение этих характеристик – выразить в сжатой форме наиболее существенные особенности распределения случайных величин. Важно, что данные параметры представляют собой конкретные (постоянные) значения, которые можно оценивать с помощью полученных в опытах данных. Этими оценками занимается «Описательная статистика».

В теории вероятностей и математической статистике используется достаточно много различных характеристик, но мы рассмотрим только наиболее употребляемые. Причем лишь для части из них приведем формулы, по которым рассчитываются их значения, в остальных случаях вычисления оставим компьютеру.

Рассмотримхарактеристики положения – математическое ожидание, моду, медиану.

Онихарактеризуют положение случайной величины на числовой оси, т.е.указывают некоторое ориентировочное значение, около которого группируются все возможные значения случайной величины. Среди них важнейшую роль играет математическое ожидание М(Х).

Математическое ожидание М(Х) случайной величины Х является вероятностным аналогом ее среднего арифметического 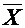(М(Х) = 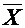или М(Х)» ).

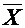Для дискретной случайной величины М(Х) вычисляется по формуле:

М(Х) = х₁р₁ + х₂р₂ +…+ х_nр_n = 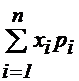. (18)

Для непрерывной случайной величины М(Х) определяют по формулам:

М(Х) = 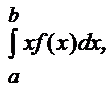или М(Х) = 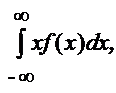(19)

где f(x) – плотность вероятности, dP = f(x)dx – элемент вероятности (аналог p_i для малого интервала Dx (dx)).

Пример: Вычислите среднее значение непрерывной случайной величины, имеющей на отрезке (a, b) равномерное распределение.

Решение: при равномерном распределении плотность вероятности на интервале (a, b) постоянна, т.е. f(х) = f_o = const, а вне (a, b) равна нулю; из условия нормировки (15) найдем значение 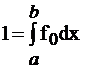f₀:

= f₀ 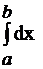= f₀ × x 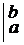= (b-a)f₀ , откуда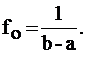

Поэтому:

M(X) = 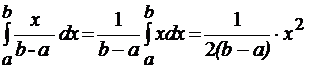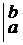= = 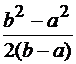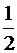(a + b).

Следовательно, математическое ожидание М(Х) совпадает с серединой интервала (a, b), определяющей 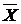, т.е. 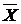= M(X) = .

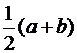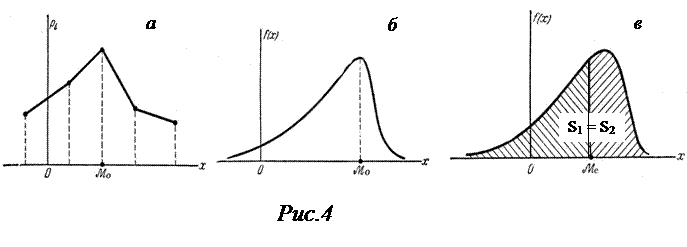
Модой Мо(Х) дискретной случайной величины называют ее наиболее вероятное значение (рис.4а), а непрерывной – значение Х, при котором плотность вероятности максимальна (рис.4б).

Медианой (Ме) случайной величины обычно пользуются только для непрерывных случайных величин, хотя формально ее можно определить и для дискретных Х. Медианой Ме(Х)случайной величины называют такое значение Х, которое делит все распределение на две равновероятные части, т.е. вероятности Р(Х < Ме) и Р(Х > Ме) оказываются равными между собой:

Р(Х < Ме) = Р(Х > Ме) = .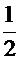

Поэтому медиану можно вычислить из соотношения:

= .

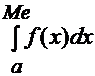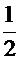Графически медиана – это значение случайной величины, ордината которой делит площадь, ограниченную кривой распределения, пополам: S₁ = S₂ (рис. 4в).

Если М(Х), Мо(Х) и Ме(Х) совпадают, то распределение случайной величины называют симметричным, в противном случае – асимметричным.

Характеристики рассеяния – это дисперсия и стандартное отклонение (среднее квадратическое отклонение)

Дисперсия D(X)случайной величины Х определяется как математическое ожидание квадрата отклонения случайной Х от ее математического ожидания М(Х):

D(X) = M[X – M(X)]² , (20)

или D(X) = M(X² ) – [M(X)]² . (21)

При конкретных расчетах для дискретной случайной величины эти формулы записываются так:

D(X) = 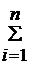[х_i–М(Х)]² × р_{i ,} или D(X) = 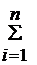х_i² р_i – [M(X)] ² (22)

Для непрерывной случайной величины, распределенной в интервале (a,b), они имеют вид:

D(X) = 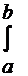[x–M(X)] ² f(x)dx, или D(X) = 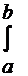х² f(x)dx – [M(X)]², (23)

а для интервала (-∞,+∞):

D(X)= 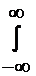[x–M(X)]² f(x)dx, или D(X)= 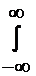х² f(x)dx– [M(X)]². (24)

Дисперсия характеризует рассеяние, разбросанность, значений случайной величины Х относительно ее математического ожидания. Само слово «дисперсия» означает «рассеяние».

Однако дисперсия D(Х) имеет размерность квадрата случайной величины, что весьма неудобно при оценке разброса в физических, биологических, медицинских и других приложениях. Поэтому обычно пользуются параметром, размерность которого совпадает с размерностью Х. Это – среднее квадратическое (иначе – стандартное) отклонение случайной величины Х, которое обозначают s (Х):

s (Х) = 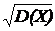. (25)

Итак, математическое ожидание, мода, медиана, дисперсия и среднее квадратическое отклонение являются наиболее употребляемыми числовыми характеристиками случайных величин, каждая из которых выражает какое-нибудь характерное свойство их распределения.