Угол между двумя прямыми и условия параллельности и перпендикулярности двух прямых. Расстояние от точки до прямой.
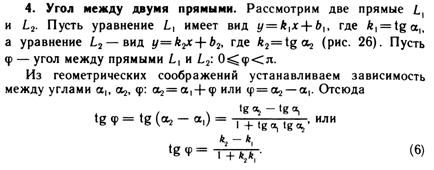

Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.
Если задано уравнение прямой на плоскости Ax + By + C = 0, то расстояние от точки M(Mx, My) до прямой можно найти используя следующую формулу
| d= | |A·Mx + B·My + C| |
| (A2 + B2)1/2 |
Уравнение линий в пространстве. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.
Как на плоскости, так и в пространстве, любая линия может быть определена как совокупность точек, координаты которых в некоторой выбранной в пространстве системе координат удовлетворяют уравнению:
F(x, y, z) = 0.
Это уравнение называется уравнением линии в пространстве.
Найдем уравнение плоскости, проходящей через точку 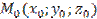 перпендикулярно вектору
перпендикулярно вектору 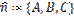 , называемому нормалью к плоскости. Для любой точки плоскости
, называемому нормалью к плоскости. Для любой точки плоскости 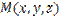 вектор
вектор 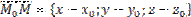 ортогонален (перпендикулярен) вектору
ортогонален (перпендикулярен) вектору 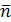 , следовательно, их скалярное произведение равно нулю:
, следовательно, их скалярное произведение равно нулю:
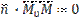 или
или 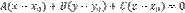 .
.
Общее уравнение плоскости. Уравнение плоскости, проходящей через три данные точки.
После преобразования, уравнение 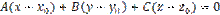
можно записать в виде 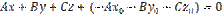 , приняв , приняв 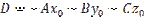 , получаем общее уравнение плоскости , получаем общее уравнение плоскости 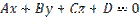 . . | |
Пусть плоскость проходит через точки 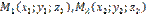 и и 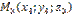 , не лежащие на одной прямой и , не лежащие на одной прямой и 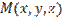 – произвольная точка плоскости. Тогда векторы – произвольная точка плоскости. Тогда векторы 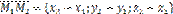 , , 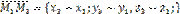 , , 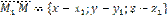 компланарны. Следовательно, их смешанное произведение равно нулю. Используя координатную запись смешанного произведения, получаем: компланарны. Следовательно, их смешанное произведение равно нулю. Используя координатную запись смешанного произведения, получаем: 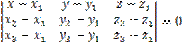 | |
Уравнение плоскости в отрезках. Нормальное уравнение плоскости.
Уравнение плоскости в отрезках
Если же общее уравнение плоскости является полным
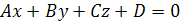
(т.е. ни один из коэффициентов не равен нулю), то его можно преобразовать к виду, называемому уравнением плоскости в отрезках
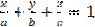 ,
,
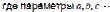 равны величинам отрезков, отсекаемых плоскостью на координатных осях.
равны величинам отрезков, отсекаемых плоскостью на координатных осях.

Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей.

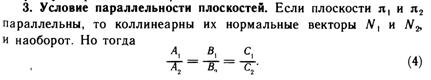
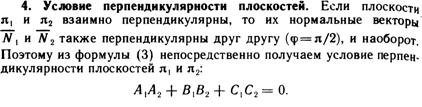
Уравнения прямой в пространстве: векторное уравнение прямой, параметрическое уравнение.
Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки М1 и вектора 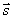 , параллельного этой прямой.
, параллельного этой прямой.
Вектор 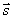 , параллельный прямой, называется направляющим вектором этой прямой.
, параллельный прямой, называется направляющим вектором этой прямой.
Итак, пусть прямая l проходит через точку М1(x1, y1, z1), лежащую на прямой параллельно вектору 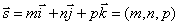 .
.
Рассмотрим произвольную точку М(x,y,z) на прямой. Из рисунка видно, что 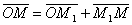 .
.
Векторы 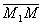 и
и 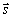 коллинеарны, поэтому найдётся такое число t, что
коллинеарны, поэтому найдётся такое число t, что 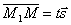 , где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М1 и М соответственно через
, где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М1 и М соответственно через 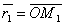 и
и 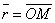 , получаем
, получаем 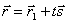 . Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки М, лежащей на прямой.
. Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки М, лежащей на прямой.

