Тема 6 ЛИНЕЙНЫЕ ЗАДАЧИ ОПТИМИЗАЦИИ

Понятие задачи Линейного Программирования. Системы линейных неравенств. Геометрический смысл области допустимых решений задачи Линейного Программирования, Целевой функция задачи Линейного Программирования. Графические методы решения классических задач Линейного Программирования: Задачи о выпуске продукции, Транспортной задачи.

2.5. Образовательные технологии

При реализации программы дисциплины «Аналитическая Геометрия» используются различные методы изложения лекционного материала в зависимости от конкретной темы – вводная, подготовительная лекции, лекции с применением техники обратной связи, лекция-беседа, лекция-дискуссия. С целью проверки усвоения студентами необходимого теоретического минимума, проводятся экспресс – тесты по лекционному материалу в письменной форме.

Практические занятия предназначены для освоения и закрепления теоретического материала, изложенного на лекциях. Практические занятия направлены на приобретение навыка решения конкретных задач, расчетов на основе имеющихся теоретических и фактических знаний

На коллоквиумах обсуждаются теоретические вопросы изучаемого курса, не включаемые в тематику практических учебных занятий.

Консультации представляют собой своеобразную форму проведения лекционных занятий, основным содержанием которых является разъяснение отдельных, часто наиболее сложных или практически значимых вопросов изучаемой программы.

Самостоятельная работа студентов направлена на закрепление полученных навыков и на приобретение новых теоретических и фактических знаний, выполняется в читальном зале библиотеки и в домашних условиях, подкрепляется учебно-методическим и информационным обеспечением (учебники, учебно-методические пособия, конспекты лекций). Практикуется самостоятельная работа по постановке и решению индивидуальных оригинальных прикладных задач. Студенты готовятся к участию в ежегодной студенческой олимпиаде по математике.

Для активизации образовательной деятельности с целью формирования и развития профессиональных навыков обучающихся, используются формы проблемного, контекстного, индивидуального и междисциплинарного обучения.

2.6. Оценочные средства для текущего контроля успеваемости, промежуточной аттестации по итогам освоения дисциплины

Общая оценка успеваемости студента по предмету выставляется за совокупный результат:

активного участия студента в практических занятиях, регулярного выполнения домашних заданий, написания экспресс - тестов по лекционному материалу (максимальное количество баллов – 20);

выполнения Контрольной работы (максимальное количество баллов – 40);

выполнения в письменной форме Домашнего задания к Практическим занятиям

№№ 4-5 и его защиты в устной форме (максимальное количество баллов - 10);

подготовленности к Коллоквиуму по теоретическому материалу и его защиты в устной форме (максимальное количество баллов - 20);

написания Индивидуальных текстовых задач экономико-управленческого содержания и решения их изучаемыми математическими методами (максимальное количество баллов – 10).

Знания студентов в семестре оцениваются по системе «зачет»: 60–100 баллов, менее 60 баллов – «незачет».

В случае не аттестации студента по курсу пересдача дисциплины осуществляется в форме традиционного зачета, на котором каждому студенту предлагаются: Вариант Контрольной работы и Тест по лекционному материалу.

Зачет считается сданным, если решено более 2-х задач и получен правильный ответ на вопрос Теста.

Таблица 1. Бальные оценки студентов.

Вид работы	Баллы
Экспресс - тесты по лекционному материалу. Активность на практических занятиях, выполнение домашнего задания.
Защита Индивидуального домашнего задания.
Защита Домашнего задания к Практическим занятиям №№4-5
Контрольная работа
Коллоквиум по теоретическому материалу

Максимально возможная сумма баллов, набираемых студентом в течение семестра, составляет - 100 баллов. Соответствие между количеством выбранных баллов и оценкой представлено в таблице 2.

Таблица 2.

Оценка	Набранные баллы
Неудовлетворительно Удовлетворительно Хорошо Отлично	0-59 60-74 75-90 91-100

Контрольная работа (текущий контроль) содержит типовые задания по ключевым темам дисциплины и проводится в конце семестра после изучения соответствующего теоретического материала.

Каждый студент получает индивидуальный вариант Контрольной работы.

Коллоквиум по теоретическому материалу проводится в конце семестра.

Защита Домашнего задания к практическим занятиям №№ 4-5 может происходить

в течение всего Семестра, но не позднее Коллоквиума.

Защита индивидуального домашнего задания может происходить в течение

всего Семестра, но не позднее Коллоквиума.

Перечень тем Контрольной работы (в письменной форме) по курсу дисциплины «Аналитическая геометрия».

1. Собственные значения Матрицы Линейного преобразования.

2. Собственные векторы Матрицы Линейного преобразования.

3. Базис системы векторов. Линейная зависимость векторов.

4. Уравнение прямой на плоскости (различные формы). Определение угла между

двумя прямыми. Условие перпендикулярности, параллельности прямых.

5. Векторная Алгебра. Расстояние между двумя точками. Деление отрезка в

данном отношении. Формула площади треугольника.

Примерный вариант Контрольной работы по курсу дисциплины «Аналитическая геометрия».

1. Найти корни характеристического уравнения, т.е. собственные числа матрицы

А =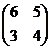

1. Найти собственные векторы матрицы Аизп.1
2. Определить, является ли данная совокупность векторов линейно зависимой.

Найти базис данной системы векторов и разложение каждого из векторов

данной совокупности в этом базисе.

.

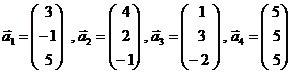1. Найти уравнение прямой, проходящей через точку пересечения прямых L1 и L2. и параллельной (перпендикулярности) прямой L3. Найти угол между прямыми L1 и L2.

L1: x – 4y +1 = 0

L2: 2x + y - 7 = 0

L3: 3x + 2y - 5 = 0

1. В треугольнике АВС с вершинами А (1, 3), В(9, -3), С(-2, -1) найти:

длины векторов АВ и АС, длину медианы АМ, уравнение высоты АR, уравнение биссектрисы АD, площадь треугольника АВС.

Перечень Контрольных вопросов по курсу дисциплины «Аналитическая геометрия».

1. Прямоугольная система координат.

2. Расстояние между двумя точками.

3. Деление отрезка в данном отношении.

4. Формула площади треугольника.

5. Уравнение прямой на плоскости (различные формы).

6. Уравнение прямой в пространстве (различные формы).

7. Определение угла между двумя прямыми. Условие перпендикулярности, условие параллельности прямых.

8. Общее уравнение плоскости.

9. Понятие вектора, определение, примеры.

10. Операции над векторами. Скалярное произведение векторов.

11. Линейно зависимые системы векторов и их свойства.

12. Линейно независимые системы векторов и их свойства.

13. Коллинеарность векторов, компланарность векторов. Базис на

плоскости и в пространстве.

14. Линейные векторные пространства: определение, примеры.

15. Базис и размерность n-мерного Линейного Пространства.

16. Ортонормированный базис.

17. Разложение любого вектора по базису.

18. Линейная зависимость и линейная независимость векторов.

19. Ранг системы векторов. Связь ранга матрицы с рангом системы векторов.

20. Евклидово пространство. Введение метрики.

21. Свойства скалярного произведения векторов.

22. Линейные операторы. Матрица Линейного преобразования.

24 Собственные значения и собственные вектора Линейных операторов.

25 Свойства собственных чисел и собственных векторов матрицы преобразования.

26 Характеристическое уравнение матрицы Линейного преобразования.

27 Теорема о существовании корней характеристического уравнения.

28 Задача об устойчивом распределении автомобилей по срокам эксплуатации.

29 Задача о нахождении равновесного вектора цен в Линейной Модели Обмена.

30 Задача о нахождении равновесного вектора национальных доходов в Модели Международной бездефицитной торговли.

31 Линейные задачи оптимизации. Системы линейных неравенств.

32 Стандартная, каноническая, общая формы задачи Линейного Программирования.

33 Область допустимых решений задачи Линейного Программирования.

34 Целевая функция задачи Линейного Программирования.

35 Классические примеры задачи Линейного Программирования –

задача о Диете, Задача о выпуске продукции, Транспортная задача.

Перечень экспресс-тестов по Лекционному материалу дисциплины «Аналитическая геометрия».

Тест 1

1. Даны две точки 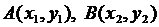. Написать выражение

для расстояния .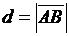

2. Написать уравнение прямой, проходящей через точку 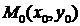и

имеющей угловой коэффициент .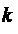

3. Написать Общее уравнение прямой на плоскости.

4. Написать условие параллельности и перпендикулярности на плоскости

двух прямых, имеющих угловые коэффициенты 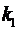и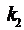

5. На отрезке 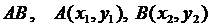дана точка С, такая, что

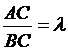Найти координаты точки С (x,y).

Тест 2

1. Написать уравнение прямой на плоскости (не ОХ, не OY),

проходящей через две точки .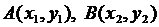

2. Даны две точки 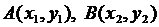. Координаты вектора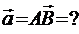

3. Даны векторы 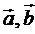. Схематично изобразить, как определяется:

а) сумма векторов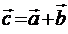

в) разность векторов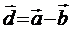

4. Дать определение коллинеарности двух векторов 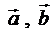. Дать определение

базиса на плоскости.

Тест 3

1 Дать определение компланарности трех векторов .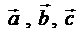

Дать определение базиса в пространстве.

2 Написать уравнение плоскости, проходящей через точку 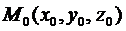и

перпендикулярной вектору нормали .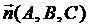

3 Написать условия параллельности и перпендикулярности 2-х плоскостей:

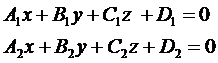в пространстве.

4 Написать Каноническое уравнение плоскости в пространстве, проходящей

через данную точку 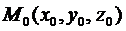и параллельной вектору .

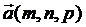Тест 4

1. Даны точки 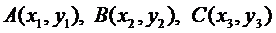. Написать условие

коллинеарности векторов 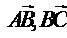через выражение для площади .

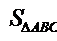2. Даны вектора .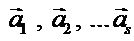

а) что такое линейно зависимая система векторов?

в) что такое линейно независимая система векторов?

3. Дать определение размерности Линейного пространства 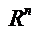, базиса

линейного пространства .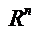

4 Дать Определение Линейного оператора .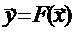

5 Дать Определение Собственного вектора 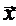и Собственного значения l

Линейного Преобразования, заданного матрицей .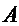

Тест 5

1 Дать Определение Характеристического уравнения для матрицы .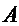

2 Как связаны Характеристическое уравнение и Собственные значения матрицы ?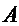

3 Сформулируйте Следствие Основной Теоремы Алгебры для Характеристического

уравнения Линейного оператора, действующего в комплексном пространстве.

4 Если 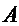- так называемая Матрица Обмена, какие 2 свойства выполнены для ее элементов?

5 Существует ли действительное собственное значение у Матрицы Обмена и какое?

Всегда ли $ собственный вектор ?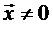

Тест 6

1. Записать Задачу Линейного Программирования в стандартной форме

( n –переменных , m – ограничений).

2. Привести Задачу Линейного Программирования в стандартной форме

к каноническому виду.

3. Записать Задачу Линейного Программирования с 2-мя переменными в

матричной форме (матрица ).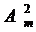

4. Как определить координаты вектора–градиента целевой функции? Что

показывает вектора–градиент?

5. Приведите свой числовой пример Задачи Линейного Программирования

с 2-мя переменными и 2-мя ограничениями.

2.7. Учебно-методическое обеспечение самостоятельной работы студентов

Список источников и литературы

Основная литература

Учебники и учебные пособия

1. Высшая математика для экономистов: учебник для студентов, обучающихся по

экономическим специальностям / Под ред. проф. Кремера Н.Ш. М.: ЮНИТИ-ДАНА,

2006-497 с.

2. Краснова С.А., Уткин В.А. Основы математического анализа: Учебное пособие

/Под ред. Кульбы В.В. М.: РГГУ, 2010 - 558 с.

3. Лунгу К.Н., Письменный Д.Т., Федин С.Н., Шевченко Ю.А. Сборник задач по

высшей математике. 1 курс. - М.: Айрис-пресс, 2007 - 576 с.

4. Экономико-математические методы и модели. Учебное пособие. /Под ред.

Макарова С.И., М.: КНОРУС. 2007 – 232с.

6. Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении.

Учебное пособие. Серия: Классический университетский учебник. - М.: Дело, 2004 –

440 с.

7. Белько И.В., Кузьмич К.К. Высшая математика для экономистов. 1 семестр.

Экспресс - курс. - М.: Новое знание, 2002 - 140 с.

Дополнительная литература

Учебники и учебные пособия

1. Воеводин В.В. Линейная алгебра. Учебное пособие. – М.: Лань, 2008. – 400 с.

2. Идельсон А.В., Блюмкина И.А. Аналитическая геометрия. Линейная алгебра.

Математика для экономистов. Том 1. Учебное пособие. - М.: ИНФРА-М, 2000 – 153 с.

3. Коршунова Н.И., Плясунов В.С. Математика в экономике. Учебное пособие.- М.:

Вита-Пресс. 1996 – 368 с..

4. Шикина Г.Е., Шикин Е.В. Гуманитариям о математике. М.: УРСС. 2001 – 272 с.

5. Пинегина М.В. Математические методы и модели в экономике. Учебное пособие. -

М.: Экзамен, 2004 - 128 с.

6. Шикин Е.В., Шикина Г.Е. Исследование операций. Учебник. М.:Изд. Проспект, 2006

280 с.

Справочные и информационныеиздания

1. Воеводин В.В., Воеводин Вл.В. Энциклопедия линейной алгебры. Электронная система ЛИНЕАЛ – СПб.: БХВ-Петербург, 2006. – 544 с.

Адреса ресурсов Интернет

1. Манаенкова Н.И. Аналитическая геометрия. / Манаенкова Н.И. Учебно-методический

комплекс [электронный ресурс] -2011-Режим доступа:

http://meu.rsuh.ru/manaenkova/manaenkova.disciplines.htm

2. Манаенкова Н.И. Линейная Алгебра. / Манаенкова Н.И. Учебно-методический

комплекс [электронный ресурс] -2011-Режим доступа:

http://meu.rsuh.ru/manaenkova/manaenkova.disciplines.htm

3. ПЛАНЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ ПО ДИСЦИПЛИНЕ

«АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ»

Пояснительная записка

Практические занятия по дисциплине «Аналитическая Геометрия» проводятся для бакалавриата дневной формы обучения по направлению подготовки № 080200 – «Менеджмент».

Цель практических занятий – способствовать лучшему усвоению и закреплению теоретических знаний, полученных из лекционного курса и изучения Литературы. Только активная самостоятельная работа студентов в ходе изучения дисциплины позволяет получить и закрепить навык использования изучаемых математических методов; применять классические методы Аналитической Геометрии для решения практических задач экономико-управленческого содержания.

Практические занятия проводятся в форме обзора новых теоретических понятий по данной теме и разбора решений типовых задач. Разбор Домашнего задания, результаты Контрольной работы позволяют выявить пробелы в знаниях и оценить уровень освоения материала.