Линейные пространства. K-мерные плоскости.
Гиперплоскости и прямые. Взаимное расположение k-мерных плоскостей.
Множество L называется линейным или векторным пространством, если для всех элементов (векторов) этого множества определены операции сложения и умножения на число и справедливо:
1. Каждой паре элементов x и y из L отвечает элемент x + yиз L, называемый суммой x и y, причём:
x + y = y + x− сложение коммутативно;
x + (y + z) = (x + y) + z− сложение ассоциативно;
x +0= x − существует единственный нулевой элемент 0( x +0= x для любого x из L);
x + (− x)= 0 − для каждого элемента x из L существует единственный противоположный элемент −x ( x + (−x) = 0для любого x из L).
2. Каждой паре x и α, где α −число, а x элемент из L, отвечает элемент α·x, наываемый произведением α и x, причём:
α·(β·x) = (α·β)·x − умножнение на число ассоциативно: ;
1·x = x − для любого элемента x из L.
3. Операции сложения и умножения на число связаны соотношениями:
α·(x + y) = α·x + α·y − умножнение на число дистрибутивно относительно сложения элементов;
(α + β)·x = α·x + β·x − умножнение на вектор дистрибутивно относительно сложения чисел.
Гиперплоскости и прямые.
Гиперплоскость — подпространство коразмерности 1 в векторном, аффинном пространстве или проективном пространстве; то есть подпространство с размерностью, на единицу меньшей, чем объемлющее пространство.
Например, для двумерного пространства гиперплоскость есть прямая (отражаемая уравнением 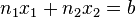 ), для трёхмерного — плоскость и т. д.
), для трёхмерного — плоскость и т. д.
Пусть задано аффинное или евклидово пространство размерности n. К-мерной плоскостьюназ-ся плоскость размерности к, т.е. она задается некоторой фиксированной начальной точкой и направляющим подпространством, т.е. к-линейно независимых векторов. 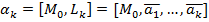 . Плоскость размерности 1 – прямая. Плоскость размерности (n-1)-гиперплоскость.
. Плоскость размерности 1 – прямая. Плоскость размерности (n-1)-гиперплоскость.
Способы задания К-мерных плоскостей: 1. 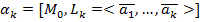 . 2.
. 2. 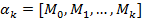 - k+1 – точкой. 3.
- k+1 – точкой. 3. 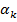 в евклидовом пространстве может быть задана точкой и ортогональным дополнением направляющего подпространства,
в евклидовом пространстве может быть задана точкой и ортогональным дополнением направляющего подпространства, 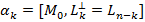 .
.
Уравнения К-мерных плоскостей:
1. Параметрическое. Пусть 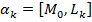 , задан базис
, задан базис 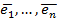 и начальная точка О. М0 будет задаваться координатами своего радиус-вектора
и начальная точка О. М0 будет задаваться координатами своего радиус-вектора 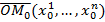 .
. 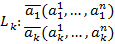 . Возьмем произвольную тHÎ
. Возьмем произвольную тHÎ 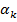 ,
, 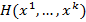 , тогда
, тогда 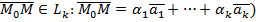 . В координатной форме
. В координатной форме 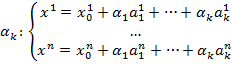 .
.
2. Общее уравнение к-мерной плоскости: 1 способ - для аффинного или евклидового пространства точечных пространств общее уравнение может быть получено из параметрических след образом: из к-параметрических ур-й выражаем пар-ры 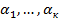 ; полученные выражения подставляем в оставшиеся (n-k)-уравнений. 2 способ – в евклидовом точеченом пространстве к-мерная плоскость задана
; полученные выражения подставляем в оставшиеся (n-k)-уравнений. 2 способ – в евклидовом точеченом пространстве к-мерная плоскость задана 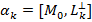 .
. 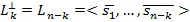 ,
, 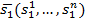 ,…,
,…, 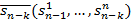 . Для любой точки М:
. Для любой точки М: 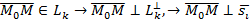 .
. 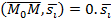 -нормальный вектор.
-нормальный вектор.
Уравнения гиперплоскостей:
1. Параметрическое. 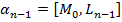 ,
, 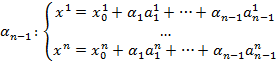 .
.
2. Общее уравнение: 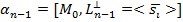 ,
, 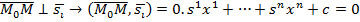 .
.
3. 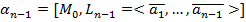 ,
, 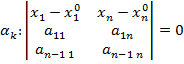 .
.
Взаимное расположение k-мерных плоскостей.
К-мерные плоскости пересекаются. 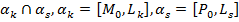 . a)
. a) 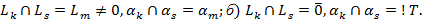
2. Параллельны: 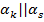 . a)
. a) 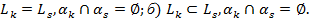
3. 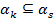 . a)
. a) 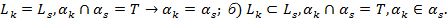
4. скрещиваются (две прямые в пространстве, не имеющие общих точек, но не являющиеся параллельными), 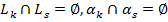 .
.
Взаимное расположение гиперплоскостей: пусть заданы 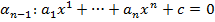 ,
, 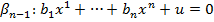 .
.
1. 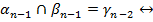 отношения их соответствующих коэф-ов не пропорциональны,
отношения их соответствующих коэф-ов не пропорциональны, 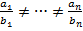 .
.
2. 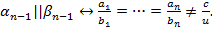
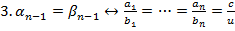 .
.
