Основные алгебраические структуры.

Группы. Кольца. Поля.

Алгеброй называется множество с операциями.

Понятие Группы.

Группой называется алгебра с одной бинарной ассоциативной операцией, относительно которой определен правый нейтральный элемент и для каждого элемента множества существует правый симметричный элемент из этого множества.

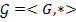- группа, если: 1). 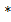- бинарная ассоциативная; 2). 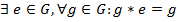; 3). .

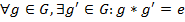Группа 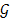называется абелевой., если бинарная операция 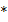, определенная на множестве 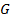является коммутативной, т.е. .

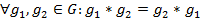Порядком группы называется количество элементов, принадлежащих основному множеству группы, или просто принадлежащих группе.

Свойства: 1).Существует единственный элемент 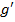, симметричный элементу 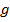группы 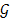; 2).В группе 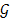существует единственный нейтральный элемент.

Группа преобразований множества.

Подгруппы

Подгруппой 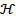группы 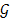называется подмножество 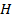множества 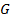, замкнутая относительно операции, определенной в группе 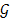. Другими словами, подгруппа группы 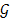сама является группой.

Смежные классы

Пусть задана группа 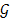и ее подгруппа .

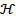Определение: произведением элемента на множество ( 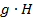) называется множество, состоящее из произведений элемента 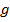на каждый элемент множества 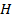, т.е. .

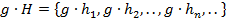Если 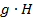(слева), то 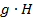- левый смежный класс группы 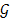по подгруппе .

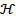Если 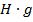(справа), то 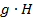- правый смежный класс группы 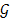по подгруппе .

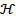ТЕОРЕМА: Смежный класс порождается любым своим элементом.

СЛЕДСТВИЕ: любые два смежных класса либо совпадают, либо не имеют общих элементов.

Определение: множество левых(правых) классов группы 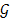по подгруппе 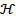называется левосторонним(правосторонним) разложением группы 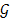по подгруппе .

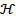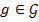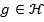Замечание: Если элемент и , то .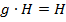

Замечание: Если группа абелева, то левостороннее разложение всегда совпадает с правосторонним разложением.

Теорема Лагранжа: Порядок 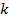подгруппы 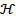конечной группы 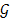делит нацело порядок 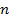группы 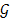(т.е. 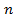делится нацело на ).

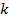Нормальная подгруппа

Подгруппа 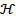группы 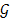называется нормальным делителем или инвариантной подгруппой, если левостороннее разложение совпадает с правосторонним.

Если 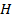- нормальный делитель, то множество 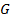группы 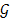можно разложить на смежные классы по нормальному делителю 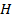. Это разложение называется фактор-множеством множества 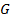по подмножеству .

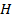Произведением множеств А и В называется множество, которое состоит из всех возможных произведений элементов множества А на элементы множества В.

Фактор-группа

Фактор-множество 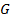по множеству 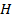с определенной на нем операцией умножения множеств является группой, которая называется фактор-группой.

Теорема: порядок фактор-группы делит нацело порядок группы.

Гомоморфизмы групп

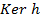- ядро гомоморфизма 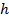- множество элементов, которые отображаются в нейтральный элемент .

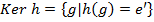Естественным гомоморфизмом называется гомоморфизм группы 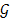на ее фактор-группу.

ТЕОРЕМА: Ядро гомоморфизма является подгруппой группы 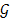, причем эта подгруппа инвариантная, т.е. 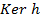- нормальный делитель.

ТЕОРЕМА (о гомоморфизмах): Пусть задан гомоморфизм группы 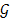в группу 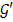, 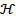- ядро гомоморфизма, тогда существует изоморфизм группы 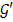на фактор-группу группы 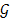по нормальному делителю 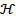такой, что композиция гомоморфизма и изоморфизма является естественным гомоморфизмом группы 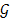на фактор-группу этой группы.

Понятие Кольца.

Непустое множество К называется кольцом, если на нем определены две бинарные операции – сложение и умножение; сложение ассоциативно и коммутативно, т.е. "(a,b,c)ÎK: a+b = b+a и (a+b)+c = a+(b+c); есть нейтральный элемент 0 относительно операции сложения; для каждого элемента есть симметричный ему элемент относительно сложения, т.е. "xÎK: (-x)ÎK,что x+(-x) = (-x)+x = 0; сложение с умножением связано дистрибутивным законом, т.е. a∙(b+c) = a∙b+a∙c (левый) и (b+c)∙a = b∙a+c∙a (правый).

Кольцо К называется кольцом с единицей, если на множестве К есть нейтральный элемент относительно умножения, т.е. "аÎK: еÎK, что а∙е = е∙а = а.

Коммутативное кольцо – кольцо, в котором операция умножения является коммутативной, т.е. "(a,b)ÎK: a∙b = b∙a.

Гомоморфизм колец (кольцевой гомоморфизм) — это отображение, сохраняющее операции сложения и умножения. А именно, гомоморфизм из кольца R в кольцо S — это функцияf:R->S, такая что 1).f(a+b)=f(a)+f(b), 2).f(ab)=f(a)f(b)

В случае колец с единицей иногда требуют также условия f(1)=1.

Гомоморфизм колец называется изоморфизмом, если существует обратный гомоморфизм колец. Любой биективный гомоморфизм колец является изоморфизмом. Автоморфизм — это гомоморфизм из кольца в себя, который является изоморфизмом. Пример: тождественное отображение кольца на себя является автоморфизмом

Если f:R->S — гомоморфизм колец, множество элементов R переходящих в ноль, называется ядром f (обозначается kerf). Ядро любого гомоморфизма является двусторонним идеалом. С другой стороны, образ f не всегда является идеалом, но является подкольцом S (обозначается imf).

Определение факторкольца по идеалу аналогично определению факторгруппы. Более точно, факторкольцо кольца R по двустороннему идеалу I — это множество классов смежности аддитивной группы R по аддитивной подгруппе I со следующими операциями: 1).(a+I)+(b+I)=(a+b)+I; 2).(a+I)(b+I)=(ab)+I.

гомоморфизм p:R->R/I задаваемый как x->x+I. Ядром при этом является идеал I

Аналогично теореме о гомоморфизме групп существует теорема о гомоморфизме колец: пусть f:R->R’ тогда Imf изоморфен факторкольцу по ядру гомоморфизма Imf ≈A/Kerf.

Примеры колец

При обычных операциях сложения и умножения кольцом является: 1).Множество целых чисел.2).Множество рациональных чисел. 3).Множество действительных чисел. 4).Множество рациональных чисел. 5). Множество, состоящее лишь из одного числа 0. 6).Множество четных чисел и вообще множество целых чисел, кратных некоторому числу n. 7).Множество комплексных чисел a + bi с целыми a и b (так называемое кольцо целых комплексных чисел). И т.д.

Понятие алгебраического Поля.

Поле P – это коммутативное кольцо с единицей 1≠ 0, в котором каждый элемент а ≠ 0 обратим.

Поле представляет собой гибрид двух абелевых групп – аддитивной и мультипликативной, связанных законом дистрибутивности.

Свойства: 1).Для любого элемента поля a∙0 = 0∙a = 0; 2).Для ненулевых элементов a и b поля a∙b ≠ 0; 3).Для любых элементов a и b поля a+b ≠ 0; 4).Если a∙b = a∙c и a ≠ 0 , то b = c .

ТЕОРЕМА: Поле делителей нуля не имеет. ДОКАЗАТЕЛЬСТВО: Пусть Р - поле, a,bÎР, a∙b=0 и a ≠ 0. Тогда по определению поля Ǝ a^-1ÎР, 0 = a^-1 ∙a∙b = 1∙b, откуда следует, что b = 0, следовательно в поле нет делителей нуля.

Теорема: Всякое конечное коммутативное кольцо без делителей нуля, содержащее более одного элемента, является полем.

Подполем F поля P называется подкольцо в P, само являющееся полем. Подполе поля Р, отличное от Р, называется собственным подполем.

Поле называется простым, если оно не имеет собственных подполей.

ПоляP и P’ называются изоморфными, если они изоморфны как кольца.

По определению f(0) = 0’ f(1) = 1’ для любого изоморфного отображения f. Не имеет смысла говорить о гомоморфизмах поле, так как Kerf≠ 0Þf(a) = 0, a ≠ 0 Þf(1) = f(aa^-1) = f(a)f(a^-1) = 0∙f(a^-1) = 0 Þ"bf(b) = f(1∙b) = f(1)f(b) = 0∙f(b) = 0 ÞKerf = P. Напротив, автоморфизмы, т.е. изоморфные отображения поля P на себя, связаны с самыми глубокими свойствами полей и являются мощным инструментом для изучения этих свойств.

Характеристика поля — наименьшее положительное целое число n такое, что сумма n копий единицы равна нулю: n∙1= 0.

Если такого числа не существует, то характеристика равна 0 по определению.