Полнота и плотность, сепараб. пр-ва. Банаховы, Гильбертовы пр-ва.
Опр(Крит. Коши):Рассмотрим в норм. пр-ве  послед. эл.
послед. эл. 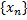 . Эл.
. Эл.  наз. пределом послед.
наз. пределом послед. 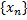 , если
, если  при
при 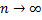 . Если
. Если 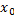 есть предел
есть предел 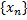 , то будем писать
, то будем писать  или
или  при
при 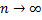 и говорить, что послед.
и говорить, что послед. 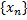 сходится к
сходится к 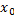 или просто сходится. Назовём окрестностью т.
или просто сходится. Назовём окрестностью т. 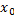 любо открытый шар
любо открытый шар  .
.
Опр: Пусть  – нормированное пр-во. Послед.
– нормированное пр-во. Послед.  наз. фундаментальной, если для любого
наз. фундаментальной, если для любого  номер
номер  такой, что для
такой, что для 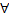 номеров
номеров  и
и 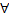 натуральных
натуральных  выполняется нерав.:
выполняется нерав.:  .
.
Опр(Банаховы пр-ва):Нормированное пр-во наз. полным, если в нём всякая фундаментальная послед. сходится. Полное нормированное пр-во наз. банаховым пространством.
Примеры:Пр-во  банахово. (Действительно, на вещ. числовой оси имеет место крит. Коши: для того чтобы послед.
банахово. (Действительно, на вещ. числовой оси имеет место крит. Коши: для того чтобы послед.  была сходящейся необходимо и достаточно, чтобы она была фундаментальной. Т.е. вся вещ. ось
была сходящейся необходимо и достаточно, чтобы она была фундаментальной. Т.е. вся вещ. ось  заполнена точками – вещ. числами, на ней нет «дыр»,т.е. что она полна.)Пр-во
заполнена точками – вещ. числами, на ней нет «дыр»,т.е. что она полна.)Пр-во  банахово, ( т.к. в
банахово, ( т.к. в  тоже справедлив критерий Коши).
тоже справедлив критерий Коши).
Опр(Линейное многообразие):Мн-во 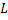 в лин. пр-ве
в лин. пр-ве  наз. лин. многообразием (лин. мн-вом), если для
наз. лин. многообразием (лин. мн-вом), если для  и любых скаляров
и любых скаляров  , линейная комбинация:
, линейная комбинация:  .
.
Опр(Аффинное многообразие):Пусть  – лин. многообразие в лин. пр-ве
– лин. многообразие в лин. пр-ве  . Фикс. т.
. Фикс. т.  . Тогда мн-во
. Тогда мн-во  наз. аффинным многообразием в
наз. аффинным многообразием в  . В трёхмерном пр-ве всякая прямая и всякая плоскость, не проходящие через начало коорд., являются аффинными многообр.
. В трёхмерном пр-ве всякая прямая и всякая плоскость, не проходящие через начало коорд., являются аффинными многообр.
Опр(Плотность): Линейное многообразие 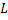 , лежащее в нормированном пр-ве
, лежащее в нормированном пр-ве  , наз. плотным в
, наз. плотным в  , если для
, если для  и
и  найдётся эл.
найдётся эл.  такой, что
такой, что  .
.
Опр(Базис): Пусть  – бесконечномерное банахово пр-во. Послед
– бесконечномерное банахово пр-во. Послед  (или
(или  наз. базисом в
наз. базисом в  , если любой эл.
, если любой эл.  может быть однозначно представлен в виде сход. ряда:
может быть однозначно представлен в виде сход. ряда:  . При этом скаляры
. При этом скаляры  наз. координатами эл.
наз. координатами эл. 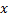 в базисе
в базисе  . Из однозначности представления (разложения)
. Из однозначности представления (разложения) 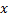 по базису вытекает лин. незав. всякого конечного набора векторов базиса.
по базису вытекает лин. незав. всякого конечного набора векторов базиса.
Опр(Сепарабельность):Нормированное пр-во  наз. сепарабельным, если в нём
наз. сепарабельным, если в нём 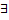 счётное, плотное в
счётное, плотное в  множество.
множество.
Примеры: Банахово пр-во со счётным базисом сепарабельно. Любое конечномерное пр-во сепарабельно ( достаточно фикс. в нём базис и рассмотреть мн-во эл. с рациональными коорд).
Опр(Гильбертовы пр-ва):Пространство со скалярным произведением наз. гильбертовым, если оно полно в норме, порождённой скалярным произведением, и обозначают буквой  .
.
Простейший пример: полное евклидово пр-во  .
.
Пусть 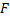 – поле чисел над которым задано скалярное произведение. Тогда если
– поле чисел над которым задано скалярное произведение. Тогда если  пр-во действительное, если
пр-во действительное, если  пр-во комплексное.
пр-во комплексное.
Пр-во  :Оно состоит из всех таких послед.
:Оно состоит из всех таких послед.  , где
, где  , для которых сходится ряд:
, для которых сходится ряд:  . Скалярное произведение и норма для векторов
. Скалярное произведение и норма для векторов  ,
,  определяются формулами:
определяются формулами:  ,
,  . Пр-во полно и содержит счётное всюду плотное множество векторов
. Пр-во полно и содержит счётное всюду плотное множество векторов  , у которых коорд.
, у которых коорд. 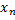 рациональны и лишь конечное их число отлично от нуля. Поэтому
рациональны и лишь конечное их число отлично от нуля. Поэтому  – сепарабельное гильбертово пр-во.
– сепарабельное гильбертово пр-во.
Пр-во  (пр-во Лебега):Пусть
(пр-во Лебега):Пусть  – это измеримое пространство с положительной мерой. Измеримые ф.
– это измеримое пространство с положительной мерой. Измеримые ф.  , у которых
, у которых  при
при  будем обозначать как
будем обозначать как  (или
(или  или
или  – пр-во Лебега. Разбивая ф.
– пр-во Лебега. Разбивая ф.  из класса
из класса  на классы эквивалентных ф.
на классы эквивалентных ф.  (Факторизация), получим класс
(Факторизация), получим класс  при
при  . Важным свойством (Для нас) является норма (точнее полунорма), определяемая формулой:
. Важным свойством (Для нас) является норма (точнее полунорма), определяемая формулой:  .По теореме Риса-Фишера, пр-во
.По теореме Риса-Фишера, пр-во  полно, т.е. любая фундаментальная послед. в
полно, т.е. любая фундаментальная послед. в  сход. к эл. этого же пр-ва. Следовательно
сход. к эл. этого же пр-ва. Следовательно  – банахово пр-во.
– банахово пр-во.
Пр-во  : В случае
: В случае  норма порождается скалярным произведением. Таким образом, вместе с понятием «длины» здесь имеет смысл и понятие «угла», а следовательно и смежные понятия, такие как ортогональность и проекция. Скалярное произведение определяется так:
норма порождается скалярным произведением. Таким образом, вместе с понятием «длины» здесь имеет смысл и понятие «угла», а следовательно и смежные понятия, такие как ортогональность и проекция. Скалярное произведение определяется так:  – интеграл Лебега при
– интеграл Лебега при  . Или проще:
. Или проще:  . А норма порождается скалярным произведением:
. А норма порождается скалярным произведением:  . Т.к. по теореме Риса-Фишера любое
. Т.к. по теореме Риса-Фишера любое  полно, то
полно, то  – гильбертово.
– гильбертово.
Опр(Ортогональность):Пусть  – пространство со скалярным произведением. Если скалярное произв.
– пространство со скалярным произведением. Если скалярное произв.  , то эл.
, то эл. 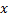 и
и  будем называть ортогональными и писать
будем называть ортогональными и писать  . Очевидно, нуль пр-ва
. Очевидно, нуль пр-ва  ортог. любому эл.
ортог. любому эл.
Опр(Ортогональные доп.): Пусть 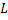 – лин. многообразие в
– лин. многообразие в  . Совокупность всех эл. из
. Совокупность всех эл. из  , ортогональных к
, ортогональных к 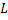 , называется ортогональным дополнением к
, называется ортогональным дополнением к 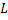 и обозначается:
и обозначается:  .
.
Теорема:  – подпространство в
– подпространство в  .
.
Таким образом, гильбертово пространство есть банахово пространство (полное нормированное пространство), норма которого порождена положительно определённым скалярным произведением и определяется как  .
.
