Ряд лорана. кольцо сходимости. правильная часть.

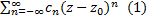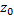Рассмотрим ряд вида: , где – фиксированная т. комплексной плоскости, 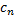– некоторые комплексные числа, а суммирование ведётся как по положительным, так и по отрицательным значениям индекса 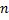. Этот ряд наз. рядом Лорана.

Представим ряд (1) в ви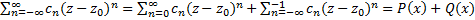де: , где 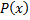– правильная часть ряда, а 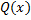– главная часть. Ряд Лорана считается сходящимся тогда и только тогда, когда сходится его правильная и главная части. Покажем это.

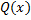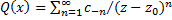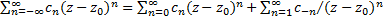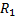Установим область сходимости. Для этого представим в несколько ином виде: . Теперь: (2). Из определения следует, что обл. сходимости ряда (1) является общая часть областей сходимости каждого из слагаемых правой части (2). Обл. сходимости является круг с центром в точке некоторого радиуса ( значение 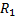может равняться 0 или 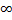. Следствие теоремы Абеля). Внутри круга сходимости этот ряд сходится к некоторой аналитической ф.компл. переменной: 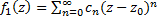, 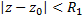. Для определения обл. сход. ряда 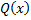сделаем замену переменной, положив 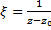. Тогда этот ряд примет вид 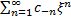. Т.е. он представляет собой обычный степенной ряд, сходящийся внутри своего круга сходимости к некоторой аналит. ф. 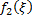комплексной переменной 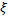. Обозначим радиус сходимости полученного степенного ряда через 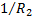. Тогда 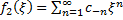, 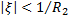. Вернёмся к старой переменной, и полагая 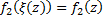, получим: , .

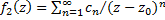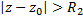Отсюда следует, что обл. сход. ряда 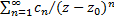по отрицательным степеням разности 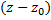является обл., внешняя к окружности 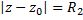( также 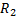, как и 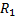, может в частности равняться 0 или 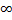). Теперь, каждый из степенных рядов сход. в своей области. Если 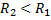, то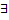

общая область сходимости этих рядов ­– круговое кольцо (кольцо сходимости) 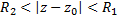в котором ряд (1) сходится к аналитической ф.: 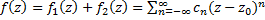, 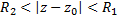. Если 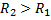, то степенные ряды общей обл. сходимости не имеют. Следовательно, ряд нигде не сходится к какой-либо ф.

Теорема Абеля.

Если степенной ряд 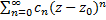сходится в некоторой т. 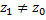, то он абсолютно сходится и любой т. 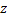, удовлетворяющей условию: 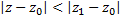; Причём в круге 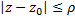радиуса 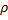меньшего 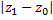, ряд сходится равномерно.

Док-во.

Выберем произвольную т. 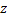, удовлетворяющей условию 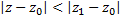; и рассмотрим ряд: 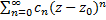. Обозначим: 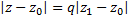, 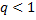. В силу необходимого условия сходимости ряда 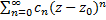его члены стремятся к нулю при 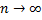. Следовательно, 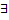такая константа 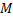, что 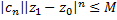. Отсюда для коэфф. 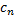получим оценку: 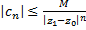. Тогда:

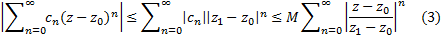
По условию 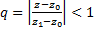. Ряд 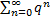, представляет собой сумму беск. геом. прогрессии со знаменателем 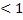, сходится. Тогда из (3) следует сходимость и рассматриваемого ряда. Чтобы доказать равномерную сходимость ряда 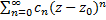в круге 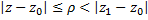, достаточно, в силу признака Вейерштрасса, построить сход. числовой ряд, мажорирующий данный функц. ряд в рассм. обл. Таковым является ряд: 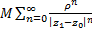, также представляющий собой сумму беск. геом. прогрессии со знаменателем .

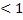Следствия:

1) Если степенной ряд 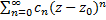расходится в некоторой т. 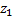, то он расходится и во всех т. 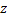, удовлервор. нерав.: .

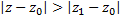2) Для всякого степенного ряда 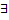такое число 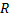, что в нутрии круга 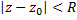данный степенной ряд сходится, а вне этого круга расходится. Также, радиус сход. в зависимости от вида коэфф. степ. ряда, может иметь любое знач. в пределах от 0 до .

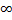3) Внутри круга сход. степенной ряд сход. к аналитической ф. Следовательно сумма ряда есть аналитическая ф.

4) Степ. ряд внутри круга сходимости можно почленно интегрировать и дифф.-ть любое число раз, причём радиус сход. полученых рядов равен радиусу исходного ряда.

Классификация особых т.

Определение 1: Т. 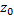называется изолированной особой т. ф. 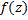, если ф. однозначная и аналитическая в круговом кольце 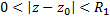, а т. 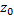является особой т. ф. 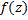. В самой т. 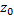ф. может быть и не определена.

Теорема: Если т. 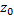является устранимой особой т. аналит. ф. 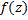, то 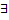предельное значение 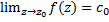, причём .

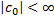Теорема(обратная пред. и более точная): Если ф. 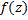, аналитическая в круговом кольце 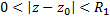, ограничена 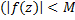при 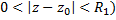, то т. 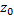есть устранимая особая т. ф. .

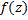Определение 2: Ряд Лорана ф. 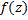в окрестности её изолированной особой т. 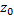содержит конечное число 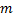членов с отрицательными степенями разности 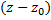, т.е. 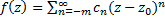. В этом случае т. 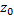называется полюсом порядка 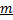функции .

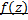Теорема(Поведение аналит. ф. в окрестности полюса): Если т. 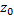является полюсом аналит. ф. 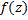, то при 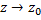модуль ф. 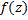неограниченно возрастает независимо от способа стремления точки 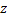к 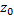. Верно и обратное.

Определение 3: Ряд Лорана ф. 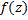. в окрестности её изолированной особой т. 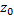содержит беск. число членной с отрицательными степенями разности 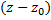, т.е. 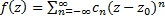. В этом случае т. 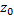называется существенно особой т. ф. .

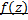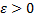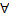Теорема(Сохоцкого – Вейерштрасса): Каково бы ни было , в окрестности существенно особой т. 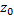ф. 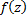найдётся хотя бы одна т. 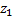, в которой значение ф. 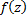отличается от произвольно заданного комплексного числа 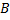больше чем на .

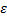Зам.: Теорема говорит о том что в сущ. особой т. не 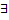конечного или беск. предельного значения аналитической ф.