Логические теории алгоритмов

Рекурсивные функции

Для ученых, которых интересуют лишь факты сущест­вования или несуществования алгоритмов, а не сами алго­ритмы, вовсе не обязательно изучать именно алгоритмы. Достаточно найти такие объекты, которые существуют или не существуют в точности тогда же, когда и алгоритмы. Считают, что такими объектами являются рекурсивные функции. Покажем, как могут функции быть связанными с алгоритмами.

Как известно, величину w называют функцией, а ве­личины x₁, х₂, ..., х_п — аргументами, или независимыми переменными, если известен закон, который для различных наборов конкретных значений величин x₁, х₂, ..., х_п за­дает определенные значения величины w. При этом для каждого набора допускается одно-единственное значение функции. В частном случае функция может иметь одно независимое переменное (аргумент). Что за закон приме­няется для определения функции? Математика не накла­дывает никаких ограничений на него. Она допускает любой мыслимый закон. Но таким законом может быть некоторый алгоритм. В этом случае функцию называют вы­числимой, так как имеется способ получения ее значений.

Рекурсивными функциями называют один частный класс вычислимых функций. Алгоритмы, являющиеся законами их задания, мы будем называть алгоритмами, сопутст­вующими рекурсивным функциям.

Напомним читателю, что, имея в виду некоторую функ­цию, нужно различать три стороны: 1) ее имя (обознача­ющую ее букву), 2) ее (функциональную) запись, имею­щую вид w=f(x₁, х₂, . . ., х_п), 3) ее значение. Буква f, присутствующая в записи функции, называется функцио­нальным знаком (кроме f в качестве функционального знака можно использовать и другие символы). Значение функции, отвечающее конкретным значениям аргументов, иногда обозначают строкой символов, которая получается из правой части функциональной записи, если имена неза­висимых переменных заменить их значениями. Например, для функции, имеющей функциональную запись, указан­ную выше в 2), ее значение, полученное при х₁=1, х₂=7,. .. . . ., х_n = 105,можно обозначить f(1, 7, . . ., 105).

Построение четко выделенного класса вычислимых функций сопряжено с рядом трудностей; для достижения такой цели нужны некоторые упрощающие соглашения. Уже в гл. 2 мы говорили о возможности арифметизировать математику, т. е. выразить самые разные математические понятия с помощью целых неотрицательных чисел. По­этому вполне естественно ограничиться случаем, в котором и независимые переменные, и функции могут принимать только целые неотрицательные значения.

Совокупность рекурсивных функций мы построим сле­дующим образом. Непосредственно опишем наиболее про­стые из них и назовем базовыми. Сопутствующие этим функциям алгоритмы будут наиболее простыми, одношаговыми. Затем опишем три приема, называемых в теории рекурсивных функций операторами, с помощью которых исходя из рекурсивных функций можно получить новые функции; их, по определению, тоже будем считать рекур­сивными. Эти операторы, по существу, будут алгоритмами; соединяя их, можно получать новые алгоритмы. Итак, строим класс рекурсивных функций.

Базовые функции бывают трех типов, а) Функ­ции любого числа независимых переменных, тождественно равные нулю. Их будем обозначать φ_n, где п — число ар­гументов. Например, к числу таких функций относятся y=φ_i(x), w=φ₃(x, у, z), w=φ_n(x_l, x₂,…, х_п). Сопутст­вующий алгоритм для этих функций гласит: «Если функциональный знак имеет вид φ_n, то любой сово­купности значений аргументов данной функции ста­вится в соответствие ее значение 0». Например, φ₁(0)=0; φ₃(3, 5, 7)=0; φ_n(7, 8, …, 125)=0.

Будем считать, что п может быть равно нулю, т. е. что возможна функция этого вида, не зависящая ни от одного аргумента. Эта функция равна 0. Обозначим ее φ₀( )[13], или, для краткости, φ₀. Аналогичную ситуацию мы видели в теории множеств: там было принято соглашение считать, что в частном случае множество может быть пустым (не содержать ни одного элемента).

б) Тождественные функции любого числа независимых переменных. Обозначим их ψ_n,i, где п — число аргументов, i — номер одного из аргументов (1≤i≤n). Сопутствующий этим функциям алгоритм гласит: «Если функциональный знак имеет вид ψ_n,i, то значением функций считать зна­чение 1-го (считая в функциональной записи слева направо) независимого переменного». Например, для функций w= ψ_3,4(x,y,z), v= ψ_1,1(u) имеем соответственног ψ_3,2(5,8,0)= =8, ψ_1,1(6)=6. А вот запись ψ_3,4(х, у, z) не имеет смысла; в ней n=3, i=4 и, следовательно, не выполнено условие 1≤i≤n. Для тождественных функций ни п, ни i не может быть равно нулю.

в) Функции следования (иначе — получения последо­вателя) одного независимого переменного. Обозначим их с помощью функционального знака λ. Например, функциями следования будут λ(х), λ(w). Сопутствующий этим функ­циям алгоритм гласит: «Если функциональный знак имеет вид λ, то значением функции считать число, непосредст­венно следующее за числом, являющимся значением аргу­мента».

Заметим, что, создавая рекурсивные функции, опираясь на которые мы хотим обосновать математику, нельзя поль­зоваться нашими знаниями даже арифметических действий. Удобно на некоторое время вообразить, что математика нами полностью позабыта (во всяком случае, до тех пор, пока мы не построим класс рекурсивных функций). Опе­рация «получения последователя», по-видимому, проще сложения. Дети сперва учатся считать, а потом уже овладевают сложением. Первобытные люди тоже сперва овладели счетом, и лишь много позже возникла идея сло­жения чисел. Это вполне естественно, так как в ту пору числа изображали как последовательности черточек (за­рубок). Последователь получали, добавляя еще одну зарубку. Мы операцию получения последователя будем обозначать с помощью штриха, например 0' = 1, 1' =2, 10' = 11 и т. д. Таким образом, λ(х)=х'; λ(5)=6.

Считается, что базовые функции имеют значения только если даны значения их аргументов.

Оператор суперпозиции или подста­новки. Слова суперпозиция и подстановка в данном случае имеют одно и то же значение. Этот оператор по функции F от п аргументов и по функциям f₁, f₂, …, f_n строит новую функцию Ф такую, что для нее справедливо тождество

.

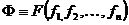Алгоритм, сопутствующий этому оператору, гласит: «Зна­чения функций f₁, f₂, …, f_n принять за значения аргу­ментов функции F и вычислить ее значение».

Например, если в качестве F принять λ(х), а в каче­стве f₁ взять функцию λ(у), то с помощью операции суперпозиции получим функцию τ(y) = λ(λ(y)) = λ(y') = y"; в частности, τ(5)=7.

Введем знак «::=», который читается как «по опре­делению есть». Оператор подстановки (суперпозиции) обо­значим буквой S. Построение функции Ф из функций F и f_i, с помощью оператора суперпозиции будем записывать так:

.

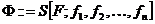Например, для нашей функции τ(у)можно написать

.

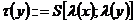Оператор рекурсии. Этот оператор по двум функциям, одна из которых имеет п — 1 независимых переменных, а другая, кроме указанных независимых переменных, имеет еще два (т. е. зависит от n+1 пере­менных), строит функцию п независимых переменных. Один из дополнительных аргументов войдет вместе с аргу­ментами первой функции в число аргументов вновь полу­чаемой функции, а другой играет вспомогательную роль при выполнении оператора рекурсии. Оператор рекурсии будем обозначать буквой R; его применение будем записы­вать в виде строки:

,

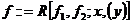где f означает получаемую функцию, f₁ — функцию п—1 независимых переменных, f₂ — функцию n+1 неза­висимых переменных, х — главный из дополнительных аргументов, у — вспомогательный аргумент.

При описании существа оператора рекурсии удобно не указывать аргументов первой из заданных функций ни в ее функциональной записи, ни в записях двух других функций, подразумевая эти аргументы. Тогда можно ска­зать, что оператор рекурсии задает функцию с помощью двух условий, в которые входят функции f₁ и f₂:

.

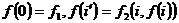Алгоритм, сопутствующий оператору рекурсии, гласит: «Значением получаемой функции для нулевого значения главного дополнительного аргумента считать значение исходной функции п—1 аргументов; значением опреде­ляемой функции для каждого последующего значения главного аргумента считать значение второй из заданных функций при предыдущем значении главного аргумента и при значении вспомогательного аргумента, совпадающем с предыдущим значением определяемой функции».

Для примера рассмотрим случай, в котором в качестве f₁ взята функция φ₀, а в качестве f₂ — функция ψ_2,1(х, у) = х. Определяемую функцию обозначим пр(х). Для нее имеем

пр(x) ::=R [φ₀, ψ_2,1(х, у); х, (у)].

Эта функция определяется условиями

пр(0)=φ₀, пр(i')= ψ_2,1(i, пр(i)),

другими словами,

пр(0)=0, пр(i')=i.

Полученная нами функция называется функцией предше­ствования; ее значениями являются пр(0)=0, пр(1)=0, пр(2) = 1, пр(3)=2 и т. д. Поскольку рекурсивные функции могут принимать только целые неотрицательные значения, то предшественником числа 0 мы считаем не —1, а 0.

Оператор построения по первому нулю (его называют обычно оператором наименьшего числа, а в некоторых книгах — оператором минимизации; по мнению автора, наше название лучше отражает его су­щество). Этот оператор по заданной функции, зависящей от п+1аргументов, строит новую функцию от п аргу­ментов. Исчезающий аргумент является вспомогательным и используется при выполнении оператора. Обозначают оператор построения по первому нулю буквой μ; его при­менение обозначают строкой вида

f::=μ[f₁; (x)],

где х — исчезающий аргумент. С помощью оператора по­строения по первому нулю получают функцию f значения которой определяются при выполнении сопутствующего ей алгоритма, который гласит: «Придавать вспомогатель­ному аргументу последовательные значения, начиная с 0, до тех пор, пока не окажется, что функция f₁ стала (в первый раз) равной нулю. Полученное значение вспомо­гательного аргумента принять за значение определяемой функции, соответствующее тем значениям основных аргу­ментов, при которых осуществлялся описанный процесс». Заметим, что базовые функции и функции, получаемые при помощи операторов подстановки и рекурсии, но без применения оператора построения по первому нулю, оп­ределены (имеют значения) для любых значений аргументов. Иначе обстоит дело с функциями, полученными при помощи оператора построения по первому нулю. Для некоторых комбинаций значений аргументов (даже для очень многих) они могут быть не определены, потому что исходная функция не принимает нулевых значений.

Для примера в качестве f₁ возьмем базовую функцию ψ_2,1(x, у). Пусть

ρ(х)::=μ[ψ_2,1(x, у); (у)].

Полученная функция ρ(х) обладает следующими свойства­ми: ρ(0)=0, ρ(i) не существует при i≠0; проверим это для случая i=2. Будем иметь ψ_2,1(2, 0)=2; ψ_2,1(2, 1)=2, ψ_2,1(2, 2)=2 и т. д. Ясно, что оператор построения по пер­вому нулю не позволит нам получить ρ(2), так как функция ψ_2,1(х, y) при x=2 ни для какого значения у не будет равной нулю.

Итак, рекурсивными называются базовые функции и любые функции, получаемые из них с помощью конечного числа операторов подстановки, рекурсии и построения по первому нулю. При этом функции, получаемые без ис­пользования оператора построения по первому нулю, на­зываются примитивно рекурсивными. Это наиболее про­стые из рекурсивных функций. Примитивно рекурсивные функции, вместе с теми рекурсивными функциями, кото­рые невозможно получить, не прибегая к оператору пост­роения по первому нулю, но которые определены для лю­бых значений аргументов, называют общерекурсивными. Оказывается, что существуют общерекурсивные функции, которые не примитивно рекурсивны. Рекурсивные функ­ции, которые определены не для всех возможных значе­ний аргументов, называют частично рекурсивными. По­строенная нами выше функция р(х) является частично рекурсивной.

Теперь, когда класс рекурсивных функций построен, можно вспомнить всю математику, которую мы на неко­торое время забыли, и посмотреть, нет ли среди хорошо знакомых нам функций рекурсивных. Оказывается есть — и немало. Например, функция у=х-1совпадает с базовой функцией λ(х) и, следовательно, рекурсивна.

С помощью оператора подстановки функции z+1 вме­сто z в функцию ψ_3,3(х, у, z)мы можем получить функцию трех переменных f*(х, у, z)=z+1, а с помощью этой функ­ции и базовой функции ψ_1,1(x)определить новую функцию s(x, у) путем рекурсии:

s(x, у)::=R[ψ_1,1(x), f*(x, y, z); y, (z)].

Эта функция удовлетворяет условиям

s(x, 0)=ψ_1,1(x)=x, s(x, 1)=s(x, 0)+1=x+1,

s(x, 2)=s(x, 1)+1=x+2, …, s(x, y)=x+y,

т. е. является функцией w=x+y. Значит, и эта функция рекурсивна. Легко показать, что и функция w=x-y ре­курсивна, и т. д. Оказывается, что многие простейшие из­вестные нам функции рекурсивны.

Американский математик А. Черч высказал мнение о том, что понятием рекурсивной функции исчерпывается поня­тие вычислимой функции. Это мнение является гипоте­зой, подтверждающейся всем предыдущим опытом мате­матиков. Она известна под названием тезиса Черча.

Тезис Черча. Какова бы ни была вычислимая неотрицательная целочисленная функция от неотрицатель­ных целочисленных аргументов, существует тождественно равная ей рекурсивная функция.

Перенося тезис Черча на алгоритмы, сопутствующие рекурсивным функциям, мы можем высказать для них следующую гипотезу.

Основной тезис. Каков бы ни был алгоритм, перерабатывающий наборы целых неотрицательных чисел в целые неотрицательные числа, существует алгоритм, сопутствующий рекурсивной функции, который ему экви­валентен.

Интересную форму этой гипотезе, вернее интересное ее обобщение, сделали советские ученые А. Н. Колмогоров и В. А. Успенский. Предположим, что нам задан некоторый алгоритм в интуитивном смысле. На практике всегда уда­ется найти способ нумерации его допустимых исходных данных, а также другой способ нумерации даваемых им результатов. Соответствие номеров исходных данных номе­рам результатов, устанавливаемое нашим алгоритмом (в интуитивном смысле), всегда совпадает с соответствием между значениями аргумента и значениями некоторой рекурсивной функции от одного независимого переменного. Это значит, что выполнение алгоритма в определенном смысле эквивалентно вычислению значения рекурсивной функции. Это значит, кроме того, что невозможность ре­курсивной функции означает и невозможность алгоритма (так как для каждого алгоритма должна быть рекурсивная функция, а ее-то в данном случае и нет).

Заметим, что тезис Черча и следующие из него осталь­ные гипотезы не имеют доказательства и принципиально не могут быть доказаны, так как в них речь идет об алго­ритмах в интуитивном смысле, не являющихся математи­ческими объектами.

Машины Тьюринга

Английский математик А. Тьюринг в 1937 г. опубли­ковал работу, в которой он уточнял понятие алгоритма, прибегая к воображаемой вычислительной машине, извест­ной теперь под названием машины Тьюринга. Идея А. Тью­ринга возникла еще до появления электронных вычисли­тельных машин и потому, по-видимому, совершенно не зависит от них.

А. Тьюринг решил, что особого внимания заслуживает поведение исполнителя алгоритма, поэтому его нужно осо­бенно точно и ясно описать. Из первой главы мы помним, что исполнитель должен действовать совершенно механи­чески, не вкладывая в свою работу никакой инициативы.

Но что или кто может в наибольшей степени обладать таким свойством? Конечно, машина. Но ресурсы реальной машины ограничены, а при выполнении алгоритмов мы их считаем неограниченными. Поэтому машина должна быть воображаемой. При желании можно будет создать реаль­ную модель машины Тьюринга, но эта модель уже будет располагать, конечно, только ограниченными ресурсами.

Итак, машина должна перерабатывать какие-то объек­ты в искомые результаты. Наиболее простыми объектами являются строки, составленные из символов. Символы, из которых образуют строки, называют в теории алгорит­мов буквами. Значение этого слова отличается от общепри­нятого. Мы знаем, что только некоторые символы называют буквами. Именно символы, служащие для записи слов естественного языка (читатель знает русские буквы, латин­ские буквы, греческие буквы). Кроме таких символов, из­вестны еще символы, применяемые для записи чисел; их называют цифрами. Наконец, читателю известны многие знаки, которые в обиходе не называют ни буквами, ни циф­рами. Таковы знаки препинания, знаки математических действий и т. п. В теории алгоритмов любые неделимые и не изменяющие своего вида знаки называют буквами.

Строки букв в теории алгоритмов называют словами. Этот термин по своему смыслу тоже отличен от общепри­нятого. Например, строку букв «аАлбмв» не считают сло­вом. В теории алгоритмов это — слово. Точно так же сло­вом является строка букв (знаков) .6;+ М— !?

В жизни принято считать словами строчки букв, явля­ющиеся словами языка, в частности, наделенные смыслом. В теории алгоритмов понятие слова не связывают с нали­чием в нем смысла. Это не значит, что слова должны быть бессмысленными. Они могут иметь смысл и даже обычно имеют какой-то смысл. Но термин «слово» означает лишь структуру объекта, построенного из символов-букв: это строка букв. Чем же обусловлен выбор слов в качестве объектов для применения к ним машин? Для их записи можно ограничиться наиболее простым техническим уст­ройством — бумажной (или магнитной, или какой-нибудь другой) лентой. Ленту будем считать бесконечной в обе стороны и разбитой на клетки равной величины. В каждой клетке может быть записана в точности одна буква. Для удобства можно считать, что пустота клетки означает на­личие в ней «пустой буквы». Обозначим пустую букву значком йо. Кроме этой буквы для данной машины долж­ны быть допустимы еще какие-то (уже не пустые) буквы. Допустим, что таких разных между собой букв еще п. Обозначим их а₁, а₂, ..., а_п.

Итак, мы имеем алфавит а₀, а₁, а₂, ..., а_п букв, которые могут быть записаны на ленте. Этот алфавит называют внешним алфавитом машины Тьюринга.

Для того чтобы передвигать ленту, машина Тьюринга снабжена простым лентопротяжным механизмом, который может либо быть неподвижным (при этом и лента непод­вижна), либо перемещать ленту на одну клетку — вправо или влево.

Для того чтобы читать написанное на ленту или писать что-либо на ней, машина Тьюринга имеет головку чтения-записи. При этом считают, что головка может за один прием прочитать только одну букву, написанную в той клетке ленты, которая расположена под головкой. Чтение буквы не изменяет того, что написано в клетке. Головка записывать может за один прием тоже только одну букву в той клетке ленты, которая стоит под головкой. При этом она сперва стирает прежнюю букву, а затем на ее месте записывает новую (может быть, в частности, одина­ковую с прежней).

Наконец, основной частью машины является логиче­ский блок. На этом блоке имеется кнопка, при нажиме которой он принимает исходное (для работы) состояние и начинает работать. Кнопка при этом остается утопленной до тех пор, пока машина не остановится сама. Тогда она «выскакивает», и машину можно использовать для новой работы. Одновременно с «выскакиванием» кнопки машина подает достаточно громкий и не очень продолжительный сигнал.

Работает логический блок следующим образом.

1) Он заставляет головку прочитать букву, которая стоит на ленте под нею.

2) В зависимости от прочитанной буквы и того состоя­ния, в котором находится он сам, а) заставляет головку записать на ленте в той клетке, которая находится под го­ловкой, некоторую букву; б) заставляет лентопротяжный механизм передвинуть ленту вправо, влево или остаться на месте, опять-таки в зависимости от прочитанной буквы и своего состояния; в) изменяет свое собственное состояние.

3) Если в результате действий, указанных в п. 2, буква, расположенная под головкой, положение ленты и состоя­ние логического блока машины окажутся теми же, которые были непосредственно перед выполнением этих действий, машина останавливается. В остальных случаях логиче­ский блок возвращается к выполнению п. 1.

Логический блок способен находиться в каждый момент в- .одном из определенных состояний. Обозначим его воз­можные состояния символами р₁, р_2, ..., р_т. Последова­тельность этих символов называют внутренним алфавитом (состояний) машины.

Введем еще обозначения d_-1, d₀, d₁ соответственно для обозначения движения ленты влево, стояния ленты на месте и движения ленты вправо. Теперь можно описать поведение машины при выполнении логическим блоком п. 2 так: если головка читает букву a_i и блок находится в состоянии p_j, то поведение машины определяет запись a_xd_yp_z, означающую: «записать на ленте вместо a_i букву а_x, совершить перемещение ленты d_y, логическому блоку перейти в состояние p_z».

Очевидно, различные машины Тьюринга отличаются друг от друга тем, как они реагируют на сочетания а_i, р_j -для разных i и j. Наиболее компактно можно представить все случаи сочетаний а_i, p_j и все виды реакций машины на них, если составить так называемую функциональную таблицу с двумя входами, в клетках которой стоят тройки символов вида a_xd_yp_z.

Читатель, наверное, обратил внимание на то, что в ма­шине Тьюринга можно различить две части: постоянную, которая одинакова для всех машин (устройство машины), и переменную, отличающую одну машину от другой (внут­ренний и внешний алфавиты и функциональная таблица).

Таблица 1

Функциональная таблица

	p1	p2	…	pj	…	pm
a0
a1
. . .
ai				axdypz
. . .
an

Если записать на ленте машины Тьюринга некоторое слово в алфавите А (внешнем), составленное из букв а₁, а₂, ..., а_п, и установить начальную букву этого слова под читающей головкой, или оставить ленту пустой (т. е. установить пустое слово), а затем нажать пусковую кноп­ку, машина начнет действовать. При этом возможны два случая: 1) работа машины после конечного числа шагов прекратится с выдачей сигнала; 2) машина никогда не остановится; никакого результата она не даст. В первом случае говорят, что машина применима к исходному дан­ному, во втором случае — что она к исходному данному неприменима.

Если машина применима к исходному данному, то она приводит к результату: а) пустому слову, если под го­ловкой находится буква а₀; б) слову из букв а₁, а₂, ..., а_п, ограниченному с двух сторон пустыми буквами, если одна из букв (непустая) этого слова находится под го­ловкой.

Соответствие, устанавливаемое машиной Тьюринга меж­ду теми исходными данными, к которым она применима, и результатами ее работы, представляет собой некоторую функцию (в математическом смысле).

Если для функции f(x) имеется машина, реализующая ее, то говорят, что f(x) вычислима по Тьюрингу. Функцию, для вычисления которой существует алгоритм, называют вычислимой. Тьюринг высказал предположение (мы будем его называть основным тезисом Тьюринга), что любая вы­числимая функция вычислима по Тьюрингу. Другими сло­вами: для любой вычислимой функции можно построить машину Тьюринга, реализующую ее.

Для примера опишем машину Тьюринга, которая вы­числяет функцию λ(х)=х+1, уже знакомую нам из пре­дыдущего параграфа (это одна из базисных рекурсивных функций). Эта функция имеет определенные значения только для целых неотрицательных значений х. Условимся значения х записывать на ленте машины в виде строки, состоящей из букв | (палочек). Кроме этих букв, нам нужна еще одна (пустая) буква. Обозначим ее знаком □ (на ленте она будет изображаться пустой клеткой). Число нуль будем изображать «пустой» строкой палочек.

Записав значение х (если оно не является нулем) в виде строки палочек на ленте машины и расположив ленту так, чтобы самая левая палочка была под головкой чтения-записи, пустим машину (нажимом кнопки).

Логический блок в начальный момент примет состоя­ние р₁ Нужно чтобы он, если головка прочитает букву |, заставил ее снова записать эту же букву, ленту — продви­нуться влево, а сам перешел снова в первое состояние (т. е. сохранил его). Если же головка прочитает букву □, а логический блок при этом будет находиться в состоянии Pi, то он должен заста­вить головку написать |, ленту — остаться на месте, а сам перейти в состоя­ние р₂.

Находясь в этом состоя­нии, он при чтении голов­кой буквы | должен застав­лять ее опять писать букву |, ленту — стоять на месте, а сам сохранять свое со­стояние р₂. Мы видим, что при этом машина остановится и подаст сигнал. Какое бы число мы ни записали на ленте, машина Тьюрин­га, двигая ленту влево, просмотрит все палочки, потом про­двинет ленту еще на один шаг, припишет к числу еще одну палочку и остановится. Функциональная таблица машины Тьюринга, вычисляющей значения функции λ(х), представлена в табл. 2.

Таблица 2

Описание работы машины Тьюринга, реализующей функцию λ(х)

	p1	p2
□	| d0p2
|	| d-1p1	| d0p2

В пустой клетке таблицы можно записать что угодно, потому что ее содержимое не влияет на работу машины. Из этой таблицы видно, что машина будет давать правиль­ный результат и при х=0. При этом под головкой машины нужно установить клетку с буквой □ (а на ленте не должно быть ни одной буквы |). После пуска машины она запи­шет вместо этой буквы букву | и остановится.

Машины Тьюринга не только соответствуют некоторым алгоритмам специального вида, но и сами являются ими. Действительно, читатель уже понял, что машины Тьюрин­га — это воображаемые машины, существующие не физи­чески, а «идеально», в наших мыслях, а точнее — в виде некоторых текстов на естественном языке. Сконструиро­вать машину Тьюринга — значит составить ее описание, а не изготовить техническое устройство. Работа машины Тьюринга заключается в том, что человек выполняет опре­деленные действия, руководствуясь описанием машины Тьюринга и ее функциональной таблицей, имея заданное начальное (подлежащее преобразованию) слово и полу­чая на очередном шаге промежуточный результат.

Таким образом, машины Тьюринга — это тексты на не­котором языке, а вовсе не машины в обычном смысле сло­ва. Эти тексты имеют «естественный смысл», присущий им как текстам естественного языка, «смысл» описаний неко­торых устройств и выполняемых ими действий. Но они имеют и второй «смысл» — математический, определяющий действия человека, якобы наблюдающего за работой ма­шины Тьюринга, а в действительности выполняющего определяемый ее «конструкцией» процесс. При этом основ­ной частью, определяющей действия исполнителя, следует считать функциональную таблицу, так как именно она определяет конкретный процесс преобразования исходного данного. Таким образом, машина Тьюринга представляет собой алгоритм, записью которого можно считать функ­циональную таблицу, а правилом (алгоритмом) выпол­нения — описание ее устройства. Приведенный выше при­мер показывает, что, в частности, можно строить машины Тьюринга для вычисления рекурсивных функций.

Основной тезис Тьюринга является аналогом уже зна­комого нам тезиса Черча. Может показаться, что машины Тьюринга приводят к более широкому понятию вычисли­мости, чем рекурсивные функции. Но это не так, потому что буквы любого алфавита можно закодировать с по­мощью двух символов 1 и 2 (метод такого кодирования описан в § 2 гл. 5) и тем самым установить соответствие между преобразованиями слов, осуществляемыми маши­нами Тьюринга, и некоторыми неотрицательными цело­численными функциями неотрицательных целочисленных аргументов.