Распределение Пуассона. Простейший поток событий

При решении многих практических задач приходится иметь дело с дискретными случайными величинами, которые подчинены закону распределения Пуассона. Типичными примерами случайной величины, имеющей распределение Пуассона, являются: число вызовов на телефонной станции, число отказов аппаратуры за некоторое время t и т.д.

Закон распределения Пуассона называют законом массовых (n велико) и редких (p мало) явлений.

Рассмотрим следующую задачу.

Задача. Найти вероятность того, что при большом числе испытаний, в каждом из которых вероятность события мала, событие наступит k раз.

Р е ш е н и е. Пусть произведение 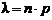сохраняет постоянное значение, это означает, что среднее число появлений события остается неизменным.

Воспользуемся формулой Бернулли:

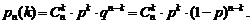(2.2)

Так как 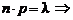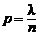, то, подставляя в равенство (2.2), получим

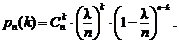(2.3)

По условию задачи n велико, поэтому в выражении (2.3) перейдем к пределу при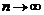

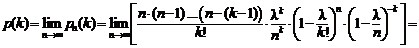
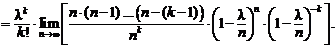(2.4)

Так как

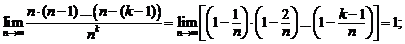
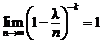и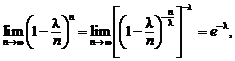

то выражение (2.4) примет вид:

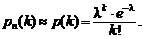
Распределение дискретной случайной величины, для которой ряд распределения задается формулой

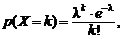(2.5)

где 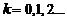называется распределением Пуассона.

Пример 1. Завод отправил на базу 500 доброкачественных изделий. Вероятность того, что изделие в пути повредится, равна 0,002. Найти вероятность того, что на базу прибудет три негодных изделия.

Р е ш е н и е. Имеем: p = 0,002, q = 1 – p = 0,998, k = 3, n = 500, т.е. n велико, p мало, поэтому эту задачу можно приближенно решить с помощью формулы Пуассона. Определим

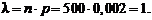
Подставляя в формулу (2.5), получим искомую вероятность

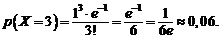
Потоком событий называется последовательность событий, которая появляется в случайные моменты времени: последовательность отказов, поступление вызовов на АТС, на пункт скорой помощи, прибытие самолетов в аэропорт и т.д.

Простейшим (пуассоновским потоком) называют поток событий, который обладает:

1) стационарностью – вероятность появления k событий на любом промежутке времени t зависит только от k и t;

2) отсутствием последствия – предыстория потока не сказывается на вероятности появления событий в ближайшем будущем;

3) ординарностью – за бесконечный малый промежуток времени может появиться не более одного события.

Интенсивностью потока 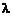называют среднее число событий, которые появляются в единицу времени.

Можно доказать, что если постоянная интенсивность потока известна, то вероятность появления k событий простейшего потока за время длительностью t определяется формулой Пуассона:

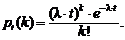(2.6)

Эта формула отражает все свойства простейшего потока.

Пример 2. Среднее число вызовов, поступающих на телефонную станцию в одну минуту, равно двум. Найти вероятность того, что за пять минут поступит четыре вызова.

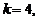
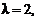
Р е ш е н и е. По условию 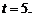Воспользуемся формулой Пуассона (2.6):

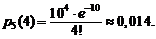
Вероятность поступления четырех вызовов за 5 минут равна 0, 014.

2.5. Геометрическое и гипергеометрическое
распределения

1. Геометрическое распределениевозникает в следующих типах задач:

а) проводятся независимые испытания;

б) вероятность появления события А в каждом испытании одинакова, т.е. ;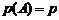

в) испытания заканчиваются, как только появится событие А.

Обозначим через X дискретную случайную величину – число испытаний, которые нужно провести до первого появления события А. Возможные значения X:

… , …

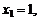
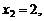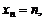Рассмотрим событие, состоящее в том, что событие А появилось в k-м испытании. Вероятность этого события по теореме умножения независимых событий:

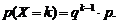(2.7)

Распределение дискретной случайной величины, описываемой формулой (2.7), называется геометрическим.

Пример 1. Вероятность поражения цели равна 0,4. Производится стрельба по цели до первого попадания. Найти вероятность того, что цель будет поражена при пятом выстреле.

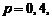
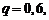
Р е ш е н и е. По условию 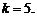Искомая вероятность по формуле (2.7) равна:

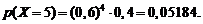
2. Гипергеометрическое распределение возникает в следующих типах задач.

Пусть в партии из n изделий m стандартных. Из партии случайным образом отбирают k изделий. Обозначим через X дискретную случайную величину – число l стандартных изделий среди k отобранных.

Возможные значения X:

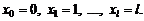
Вероятности принятия этих возможных значений:

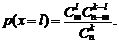(2.8)

Распределение дискретной случайной величины, описываемое формулой (2.8), называется гипергеометрическим.

Пример 2. В лотерее «Спортлото 6 из 45» денежные призы получают участники, угадавшие 3, 4, 5 и 6 видов спорта, отобранных случайно из 45. Найти закон распределения случайной величины X – числа угаданных видов спорта среди отобранных шести и вероятность получения денежного приза.

Р е ш е н и е. Случайная величина 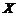имеет гипергеометрическое распределение с параметрами 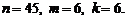Ряд распределения, рассчитанный по формуле (2.8), имеет вид:

X							. 6
p	0,40056	0,42413	0,15147	0,02244	0,00137	0,00003	0,0000001

Вероятность получения денежного приза:

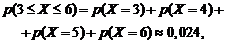
т.е. равна сумме вероятностей угадывания 3, 4, 5 и 6 видов спорта.