Определение вероятности и ее основные свойства

Так как частоту события можно определить только после проведения испытаний (опытов) и в различных опытах она может получаться величиной непостоянной, поэтому эта характеристика события является неполной и неудобной.

Однако по мере увеличения числа испытаний частота постепенно стабилизируется и колеблется около некоторой постоянной величины. Эта постоянная величина называется вероятностью и обозначается р(А), или просто р. Такое определение вероятности называется статистическим.

Преимущество статистического определения: опирается на реальный эксперимент. Недостаток: необходимо проделать большое число испытаний, не является строгим с точки зрения математики, поэтому существует другое определение вероятности,классическое.

Определение (классическое).Вероятностью появления некоторого события А называется отношение числа случаев, благоприятствующих появлению события A(m), к общему числу равновозможных в опыте случаев (n):

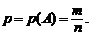(1.2)

Пример 1. Найти вероятность того, что при бросании игральной кости, выпадет четное число очков.

Р е ш е н и е.Обозначим через A событие выпадение четного числа очков. Число всех равновозможных случаев n = 6. Число благоприятствующих случаев m = 3. Поэтому

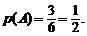
Пример 2. В урне находится 15 шаров, из них 9 красных и
6 синих. Найти вероятность того, что извлеченный наугад 1 шар окажется красным.

Р е ш е н и е. Обозначим через А событие, состоящее в появлении красного шара, т.е. A={шар красный}.

Число случаев, благоприятствующих появлению события А, равно числу красных шаров в урне, т.е. m = 9. Общее число равновозможных случаев равно общему числу шаров в урне, т.е. n = 15. Следовательно, по формуле (1.2)

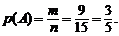
Таким образом, вероятность – это количественная характеристика события, являющаяся следующим основным понятием теории вероятностей.

И, наконец, существует третье определение вероятности – аксиоматическое.

Определение (аксиоматическое). Числовая функция p, определенная на алгебре событий F, называется вероятностью, если удовлетворяет следующим аксиомам:

А к с и о м а 1. Вероятность любого события заключена между нулем и единицей, т.е.

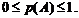
А к с и о м а 2. Вероятность достоверного события равна единице, т.е.

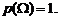
А к с и о м а 3. Вероятность невозможного события равна нулю, т.е.

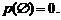
А к с и о м а 4. Вероятность суммы (объединения) двух несовместных событий А и В равна сумме вероятностей этих собы-
тий, т.е.

.

Эта аксиома вводится на основании четвертого свойства частоты. Для введения пятой аксиомы, соответствующей пятому свойству частоты, введем определение условной вероятности.

Вероятность наступления события А, вычисленная при условии наступления другого события В, называется условной вероятностью события А и обозначается:

.

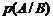Например, вероятность выпадения двойки при бросании игральной кости равна 1/6, условная вероятность выпадения двойки при условии, что выпадает четное число, равно 1/3, т.е.

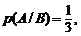
где А ={выпадение двойки}; B = {выпадение четного числа очков}.

А к с и о м а 5. Вероятность произведения (пересечения) двух совместных событий А и В равна произведению вероятности одного из них на условную вероятность другого, т.е.

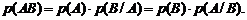
Следствие 1. Сумма вероятностей противоположных событий равна 1, т.е. .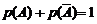

Следствие 2. Если события A₁, A₂, …, A_n образуют полную группу несовместных событий, то сумма их вероятностей равна 1, т.е.

.

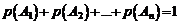1.5. Комбинаторный метод вычисления вероятностей
по классической формуле

По классическому определению вероятность события определяется по формуле:

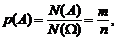(1.3)

где 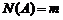– число случаев, благоприятствующих появлению события А; 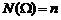– общее число равновозможных случаев.

При вычислении вероятности по этой формуле часто используют основные правила и формулы комбинаторики.

Сформулируем два важных правила.

1.Правило суммы. Если элемент А₁ может быть выбран n₁ способами, элемент А₂– n₂ способами и т.д., А_k – n_k способами, то выбор одного из элементов: или А₁, или А₂, или …, или А_k может быть осуществлен 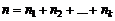способами.

Пример 1. Сколько различных трехзначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, чтобы каждое число содержало цифру 1 ровно 2 раза.

Р е ш е н и е. Две единицы содержат трехзначные числа вида:

; ;

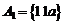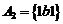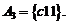
Числа вида A₁ могут быть составлены 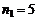способами, вида А₂ – n₂= 5 способами, вида 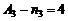способами. По правилу суммы всего таких чисел можно составить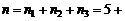

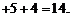
2.Правило умножения. Если элемент A₁ может быть выбран n₁ способами, после каждого такого выбора элемент A₂ может быть выбран n₂ способами и т.д., после каждого (k–1) выбора элемент A_k может быть выбран n_k способами, то выбор всех элементов 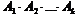в указанном порядке может быть осуществлен 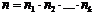способами.

Пример 2. Сколько различных трехзначных чисел, делящихся на 5, можно составить из цифр 0, 1, 2, 3, 4, 5.

Р е ш е н и е. Трехзначное число – это комбинация вида (a, b, c), где на месте a могут быть числа 1, 2, 3, 4, 5, т.е. 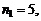на месте b – 0, 1, 2, 3, 4, 5, т.е. 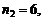а на месте с – 0 и 5, т.е. 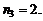По правилу умножения всего таких чисел можно составить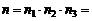

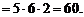
Различают три типа комбинаций: размещение, сочетание и перестановка.

Размещениями из n элементов по k называются упорядоченные подмножества k элементов множества, отличающиеся либо составом элементов, либо порядком их расположения (либо и тем и другим). Число размещений из n элементов по k равно:

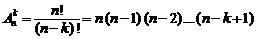. (1.4)

Сочетаниями из n элементов по k называются неупорядоченные подмножества k элементов множества, отличающиеся только составом элементов. Число сочетаний из n элементов по k равно:

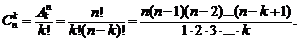(1.5)

Если комбинации из n элементов отличаются только порядком расположения этих элементов, то их называют перестановками из n элементов. Число перестановок из n элементов равно:

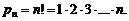(1.6)

Пример 3. Задано множество из трех букв (a, b, c). Составить все сочетания и размещения из трех букв по 2 и найти все перестановки.

Р е ш е н и е. Число сочетаний и их представление:

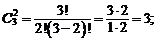
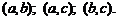
Число размещений и их представление:

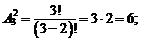
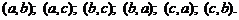
Число перестановок и их представление:

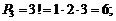
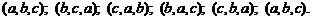
Если в размещениях (сочетаниях) из n элементов по k некоторые из элементов (или все) могут оказаться одинаковыми, то такие размещения (сочетания) называют размещениями (сочетаниями) с повторениями из n элементов по k.

Число размещений с повторениями из n элементов по k равно:

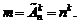(1.7)

Число сочетаний с повторениями из n элементов по k равно:

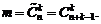(1.8)

Пример 4. В конкурсе по 5 номинациям участвуют 10 кинофильмов. Сколько существует вариантов распределения призов, если по каждой номинации установлены: а) различные призы;
б) одинаковые призы?

Р е ш е н и е. а) Каждый из вариантов распределения призов представляет собой комбинацию 5 фильмов из 10, отличающуюся от других комбинаций как составом фильмов, так и их порядком по номинациям (или тем и другим), причем одни и те же фильмы могут повторяться несколько раз, так как любой фильм может получить призы как по одной, так и по нескольким номинациям, т.е. представляет размещение с повторениями из 10 элементов по 5. Их число по формуле (1.7) равно:

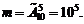
б) Если по каждой номинации установлены одинаковые призы, то порядок следования фильмов в комбинации 5 призеров значения не имеет, и число вариантов распределения призеров представляет собой число сочетаний с повторениями из 10 элементов
по 5, определяемое по формуле (1.8):

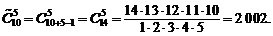
Если в перестановках из общего числа n элементов есть k различных элементов, при этом 1-й элемент повторяется n₁ раз, 2-й элемент– n₂ раз, … k-й элемент – n_k раз, причем 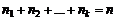, то такие перестановки называют перестановками с повторениями из n элементов. Число перестановок с повторениями из n элементов равно:

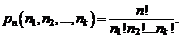(1.9)

Пример 5. Сколько существует семизначных чисел, состоящих из цифр 4, 5, 6, в которых цифра 4 повторяется 3 раза, а цифры 5 и 6 – по 2 раза?

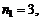
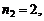
Р е ш е н и е. Каждое семизначное число отличается от другого порядком следования цифр, т.е. является перестановкой с повторениями из 7 элементов, причем 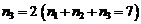. Их число по формуле (1.9) равно:

.

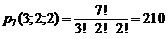Существуют две схемы выбора – с возвращением каждого элемента в совокупность и без возвращения. В результате получаются следующие четыре различные постановки эксперимента по выбору наудачу k элементов и общего числа n различных элементов.

1. Схема выбора, приводящая к сочетаниям. Если опыт состоит в выборе k элементов из n имеющихся без возвращения и без упорядочивания, то получаемые при этом комбинации будут сочетаниями из n элементов по k, а их общее число определяется по формуле:

.

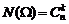Пример 6. В урне 5 белых и 10 красных шаров. Наугад извлекают 2 шара. Найти вероятность того, что оба шара белые.

Р е ш е н и е. Пусть событие А = {оба шара белые}, тогда по формуле (1.3):

,

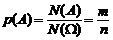где ; .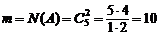

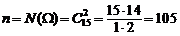Итак,

.

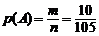2. Схема выбора, приводящая к размещениям. Если опыт состоит в выборе k элементов из n без возвращения, но с упорядочиванием их по мере выбора, то общее число элементарных исходов будет определяться по формуле:

.

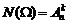Если 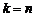, то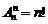

Пример 7. В мешочке имеется пять одинаковых кубиков. На всех гранях кубика написана одна из букв: «п», «о», «р», «с», «т». Найти вероятность того, что на вынутых по одному и расположенных в линию кубиках можно прочесть слово «спорт».

Р е ш е н и е. Пусть событие A – получение слова «спорт». Различные комбинации пяти букв из имеющихся пяти представляют размещения, так как могут отличаться как составом входящих букв, так и порядком их следования (или и тем и другим), т.е. общее число случаев 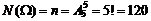, из которых благоприятствует событию А только один случай, т.е. m = 1. По формуле (1.3):

.

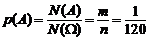3. Схема выбора, приводящая к сочетаниям с повторениями. Если опыт состоит в выборе с возвращением 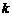элементов из 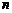, но без последующего упорядочивания, то общее число элементарных исходов будет определяться по формуле:

.

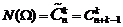Пример 8. В кондитерской имеется 7 видов пирожных. Очередной покупатель выбил чек на 4 пирожных. Считая, что любой заказываемый набор пирожных равновероятен, вычислить вероятность того, что покупатель заказал: а) пирожные одного вида;
б) пирожные разных видов.

Р е ш е н и е. а) Число всех равновозможных исходов, очевидно, равно числу сочетаний с повторениями из 7 по 4, т.е.

.

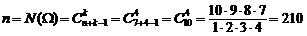Пусть событие А = {пирожные одного вида}, В = {пирожные разных видов}. Число исходов, благоприятствующих событию А, равно числу способов выбрать один элемент из семи, поэтому 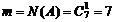. По формуле (1.3):

.

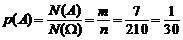б) Число исходов, благоприятствующих событию В, равно числу способов отобрать без возвращения 4 элемента из 7, поэтому

.

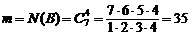По формуле (1.3):

.

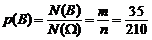4. Схема выбора, приводящая к размещению с повторениями. Если опыт состоит в выборе 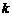элементов из 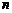с возвращением и упорядочиванием, тогда общее число равновозможных исходов будет определяться по формуле:

.

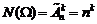Пример 9. В группе 10 человек. Найти вероятность того, что хотя бы у двух студентов дни рождения совпадают.

Р е ш е н и е. Пусть событие А – дни рождения хотя бы двух студентов совпадают. Найдем вероятность противоположного события 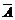– дни рождения всех студентов различны.

Число случаев, благоприятствующих событию 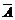, есть число размещений из 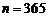элементов (дней года) по 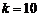, т.е. 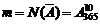. Общее число случаев определяется также числом размещений из 365 по 10, но размещений с повторениями, т.е.

.

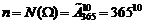Согласно классическому определению вероятности

.

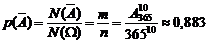Вероятность события А: 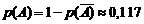.