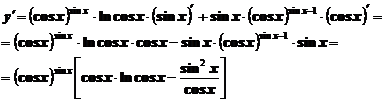ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ №1

I. При вычислении пределов следует учитывать следующие основные правила:

1. Предел суммы (разности) функций равен сумме (разности) пределов слагаемых:

.

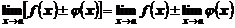2. Предел произведения функций равен произведению пределов сомножителей:

.

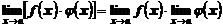3. Предел отношения двух функций равен отношению пределов этих функций:

.

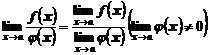4. Постоянный множитель можно выносить за знак предела:

.

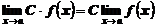5. Предел постоянной равен самой постоянной:

.

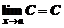6. Для непрерывных функций символы предела и функции можно поменять местами:

.

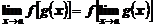Нахождение предела функции 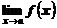следует начинать с подстановки значения 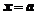в выражение для функции. При этом, если получается числовое значение, 0 или ¥, то искомый предел найден. Если получается неопределенной выражение, то для нахождения предела нужно преобразовать функцию так, чтобы раскрыть эту неопределенность.

Пример 1. Вычислить предел .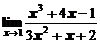

.

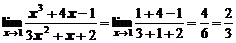Неопределенность вида обычно получается, когда задан предел отношения двух многочленов. В этом случае, для вычисления предела рекомендуется разложить многочлены на множители и сократить на общий множитель. Этот множитель равен нулю при предельном значении х.

Пример 2. Вычислить предел .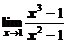

Подставляя 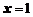получим неопределенность:

.

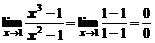Разложим числитель и знаменатель на множители:

;

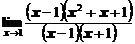Сократим на общий множитель 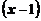и получим

.

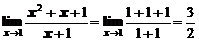Неопределенность вида 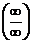получается, когда задан предел отношения двух многочленов при 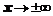. В этом случае для вычисления рекомендуется разделить оба многочлена на х в старшей степени.

Пример 3. Вычислить предел .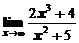

.

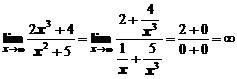Здесь учитывается, что .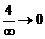

При вычислении пределов, содержащих корни, рекомендуется умножить и разделить функцию под знаком предела на сопряженное выражение.

Пример 4.

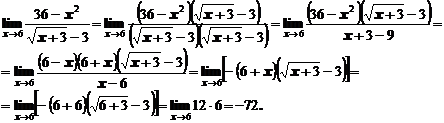
При вычислении пределов часто используются первый и второй замечательные пределы:

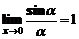
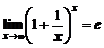и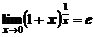

В последующем примере путем преобразования выражения выделяется первый замечательный предел.

Пример 5. При непосредственном вычислении получаем неопределенность вида .

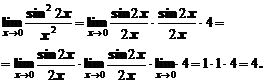
Пример 6. Вычислить предел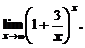

Здесь получается неопределенность вида 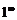. Для вычисления предела введем новую переменную 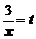. Отсюда 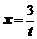, при 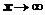, 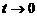. Итак, получим

.

Пример 7. Вычислить предел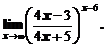

Сделаем простые преобразования для того, чтобы выделить целую часть дроби равную 1:

,

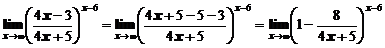Сделаем замену 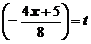, и преобразуем степень, чтобы получить второй замечательный предел

.

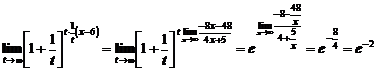Для раскрытия неопределенности вида или 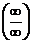также можно использовать правило Лопиталя, которое основано на следующей теореме.

Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных

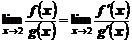
Заметим, что это правило можно применять несколько раз подряд.

Пример 8. Найти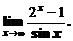

Здесь получается неопределенность вида . По правилу Лопиталя получим

Пример 9. Найти предел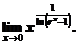

Представляя 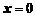, получим неопределенность вида 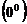. В подобных случаях можно использовать следующий прием.

Обозначим

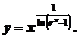
Прологарифмируем это выражение

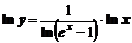
Найдем предел от обеих частей

Подставляя 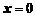, получим неопределенность вида 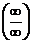. Применим правило Лопиталя:

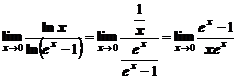
Подставляя 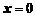, получим неопределенность вида . Применим еще раз правило Лопиталя:

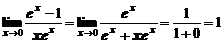
Теперь, учитывая, что функция 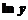непрерывна, поменяем местами операции:

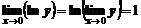
отсюда получим

Итак,

.

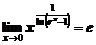II. При вычислении производных следует учитывать основные правила дифференцирования:

1. Постоянный множитель можно выносить за знак производной:

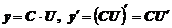(1)

2. Производная суммы (разности) функций равна сумме (разности) производных этих функций:

(2)

3. Производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:

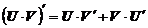(3)

Это правило справедливо для случая нескольких сомножителей.

4. Производная отношения двух функций равна дроби, в числителе которой разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а в знаменателе квадрат исходного знаменателя:

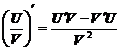(4)

5. Если 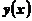сложная функция, т.е. 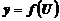, а ,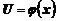

то производная 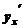находится, как 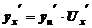(5)

Пример 10. Найти производную функции .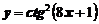

Обозначим 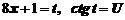, тогда получим .

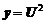Воспользуемся правилом 5 и таблицей производных (приложение 1).

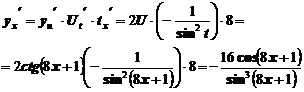
Пример 11. Найти производную функции .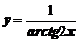

Рассматривая функцию как сложную и пользуясь правилом (4), получим

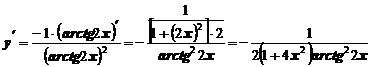
Пример 12. Найти производную функции .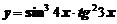

Рассматривая функцию как сложную и учитывая правило (3), получим

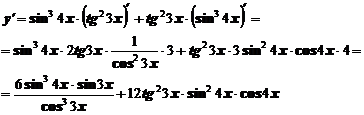
Иногда, чтобы облегчить нахождение производной логарифмической функции предварительно нужно сделать ее преобразования, учитывая правила логарифмирования.

Пример 13. Найти производную функции ;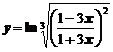

Сделаем преобразование функции

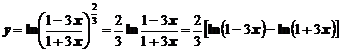
Найдем производную, учитывая правило (2) и рассматривая каждый логарифм, как сложную функцию

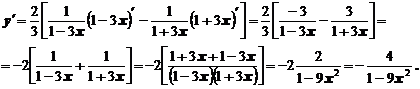
Если дана функция вида 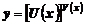, причем 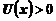, то ее производная находится по формуле,

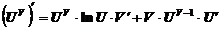
Пример 14.Найти производную функции