Правила и порядок выполнения

МАТЕМАТИКА

Методические указания

по выполнению контрольных работ

для студентов 1-го курса заочной формы обучения

всех специальностей экономического факультета

Часть 1

Кемерово 2008

Утверждено на заседании кафедры высшей и прикладной математики Кемеровского института (филиала) ГОУ ВПО «РГТЭУ». Протокол №2 от 22.09.2008 г.

Рекомендовано к печати Учебно-методической комиссией по математическим и информационным дисциплинам Кемеровского института (филиала) ГОУ ВПО «РГТЭУ». Протокол №2 от 22.09.2008 г.

Математика[Текст]: Методические указания по выполнению контрольных работ для студентов 1-го курса заочной формы обучения всех специальностей экономического факультета /Сост.: С.Н. Астраков, Л.Н. Гавришина, Н.А. Жеребцова. – Кемерово: Кемеровский институт (филиал) ГОУ ВПО «РГТЭУ», 2008. – 79 с.

В методических указаниях представлены рабочая программа по дисциплине «Математика», вопросы для экзамена, четыре контрольные работы, в соответствии с учебным планом и методические указания по их выполнению. Приводится краткий теоретический материал и подробное решение ряда задач.

Составители:

к.ф.-м.н., доцент

Астраков С.Н.,

к.ф.-м.н., доцент

Гавришина Л.Н.,

к.т.н., доцент

Жеребцова Н.А.

ЦЕЛЬ ИЗУЧЕНИЯ ДИСЦИПЛИНЫ

С появлением товарно–денежных отношений возникает необходимость количественной оценки операций и анализа их эффективности. Уже в XIX веке в отдельную отрасль знаний выделилась «Коммерческая арифметика», включающая в себя процентные вычисления по вкладам и ссудам и по операциям с ценными бумагами. Тогда же появляются первые работы, исследующие экономические процессы с помощью математических методов. В XX веке такие исследования приобретают еще большее значение, во-первых, в связи с развитием собственно математической теории, и, во-вторых, с появлением электронных вычислительных машин, позволивших применить эти теории для решения экономических задач, возникающих на практике. В настоящее время дальнейшее развитие электронных технологий сделало применение математических методов исследования экономических операций еще более актуальным.

Возросшее в условиях усиливающейся конкуренции информационно-технологическое обеспечение коммерческой деятельности предприятий и фирм выдвигает на первый план количественный и качественный анализ, оценку эффективности и задачу оптимизации этой деятельности, что в свою очередь требует все возрастающего уровня математической подготовки соответствующих специалистов. Этим обусловлена необходимость введения курса математики для изучения студентами данных экономических специальностей.

Курс математики занимает особое место в структуре учебных планов для данных экономических специальностей по следующим причинам. Во-первых, он используется для изучения ряда других дисциплин, входящих в учебные планы (статистика), во-вторых, позволяет глубже понять и усвоить другие курсы, формально независимые от него, в-третьих, имеет самостоятельное значение для развития общего интеллектуального уровня студентов.

Цель курса состоит в изучении основных структур математического анализа и овладении математическими методами в экономике. Параллельно решается задача научить студентов применять полученные знания на практике.

ПРАВИЛА И ПОРЯДОК ВЫПОЛНЕНИЯ

КОНТРОЛЬНЫХ РАБОТ

1. В процессе изучения дисциплины «Математика» студент должен выполнить четыре контрольные работы. Не следует приступать к выполнению контрольного задания до решения достаточного количества задач по учебному материалу, соответствующему этому заданию. Опыт показывает, что чаще всего неумение решить ту или иную задачу контрольного задания вызывается тем, что студент не выполнил это требование.

2. Контрольные работы должны быть оформлены в соответствии с настоящими правилами. Работы, выполненные без соблюдения этих правил, не засчитываются и возвращаются студенту для переработки.

3. Каждую контрольную работу следует выполнять в отдельной тетради, чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента.

4. На обложке тетради должны быть разборчиво написаны фамилия, имя, и отчество студента, факультет (институт), номер группы, название дисциплины, номер контрольной работы, номер варианта и домашний адрес студента. В конце работы следует поставить дату ее выполнения и расписаться.

5. Номер варианта контрольной работы, которую выполняет студент, должен совпадать с последней цифрой номера его зачетной книжки.

6. Решения задач надо располагать в порядке возрастания номеров. Условия задач следует переписать в тетрадь.

7. При решении задач нужно обосновать каждый этап решения, исходя из теоретических положений курса.

Решение задач и примеров следует излагать подробно, объясняя все выполненные действия и используемые формулы.

Полученный ответ следует проверить способами, вытекающими из существа данной задачи.

8. Срок проверки контрольных работ - 10 рабочих дней. Студенты обязаны сдавать письменные контрольные работы не позднее, чем за 10 дней до начала экзаменационной сессии. В противном случае они не будут допущены к экзамену.

9. После получения прорецензированной работы студент должен исправить все отмеченные рецензентом ошибки и недочеты, внести в решения задач рекомендуемые рецензентом изменения или дополнения и прислать работу для повторной проверки. Для этого рекомендуем при выполнении контрольной работы оставить в конце тетради несколько чистых листов.

Вносить исправления в сам текст работы после ее рецензирования запрещается.

На экзамен студент допускается при наличии проверенных контрольных работ.

ТЕМАТИЧЕСКИЙ ПЛАН ДИСЦИПЛИНЫ

1 семестр

1. Дифференциальное исчисление.

2. Интегральное исчисление.

3. Дифференциальные уравнения. Ряды.

2 семестр

4. Аналитическая геометрия.

5. Линейная алгебра.

6. Элементы теории вероятностей.

3 семестр

7. Линейное программирование.

4 семестр

8. Транспортная задача.

9. Матричные игры.

10. Теория массового обслуживания.

РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ

1 семестр

Раздел 1. Дифференциальное исчисление

Множество действительных чисел. Понятие функции. Способы задания функций. Классификация функций. Числовая последовательность и ее предел. Предел функции. Бесконечно большие и бесконечно малые функции. Основные теоремы о пределах. Два замечательных предела. Односторонние пределы функции. Непрерывность функции. Приращение функции. Классификация точек разрыва. Свойства непрерывных функций. Понятие производной. Геометрический и физический смысл производной. Основные правила дифференцирования. Производная сложной и обратной функции. Производные высших порядков. Понятие дифференциала функции. Геометрический смысл дифференциала. Правило Лопиталя. Определение экстремумов функции. Признаки постоянства, возрастания и убывания функции. Достаточные признаки существования экстремума функции. Направление выпуклости графика функции. Точки перегиба. Асимптоты. Общая схема исследования функции.

Раздел 2. Интегральное исчисление

Первообразная. Неопределенный интеграл и его свойства. Таблица основных интегралов. Основные методы интегрирования: непосредственное интегрирование, замена переменной, интегрирование по частям. Понятие определенного интеграла. Формула Ньютона-Лейбница. Свойства определенного интеграла. Методы интегрирования. Геометрические приложения определенного интеграла: площадь плоской фигуры, объем тела вращения.

Раздел 3. Дифференциальные уравнения. Ряды

Понятие о дифференциальном уравнении. Порядок дифференциального уравнения. Семейство решений. Геометрическое истолкование решения. Задача Коши. Общее и частное решения. Метод решения уравнения с разделяющимися переменными и линейного уравнения первого порядка. Числовые ряды. Понятие сходимости ряда. Знакоположительный и знакочередующийся ряд. Необходимое и достаточные условия сходимости ряда. Признак Даламбера, Коши, Лейбница. Степенные ряды. Радиус и область сходимости. Ряд Маклорена. Разложение элементарных функций в ряд Маклорена.

2 семестр

Раздел 4. Аналитическая геометрия

Введение. Основные понятия аналитической геометрии. Общее уравнение прямой на плоскости. Уравнение прямой, проходящей через две точки. Уравнение прямой с угловым коэффициентом. Условия параллельности и перпендикулярности прямых. Угол между двумя прямыми. Расстояние от точки до прямой.

Раздел 5. Линейная алгебра

Основные понятия линейной алгебры. Определитель n-го порядка. Свойства определителей. Способы вычисления. Миноры, алгебраические дополнения. Матрицы. Операции над матрицами. Системы линейных уравнений. Основные понятия. Методы решения системы n - линейных уравнений с n – неизвестными: Гаусса, Крамера, матричный.

Раздел 6. Элементы теории вероятностей

Основные понятия теории вероятностей. Случайные события. Относительная частота. Определение вероятности. Алгебра событий. Основные формулы комбинаторики. Теорема сложения вероятностей. Теорема умножения вероятностей. Независимость событий. Формула полной вероятности и формула Бейеса. Формула Бернулли. Локальная и интегральная теоремы Лапласа. Понятие случайной величины. Дискретная и непрерывная случайная величина. Ряд распределения, функция распределения дискретной случайной величины, ее числовые характеристики. Основные распределения случайных величин.

3 семестр

Раздел 7. Линейное программирование

Задачи линейного программирования. Примеры экономических задач, приводящих к модели линейного программирования. Общая задача линейного программирования (ЗЛП). Основные понятия. Экономико-математическая модель ЗЛП. Графическое решение ЗЛП. Симплекс-метод решения ЗЛП. Преобразование общей модели в каноническую. Признак оптимальности опорного решения в случае нахождения максимума целевой функции. Симплекс-метод решения ЗЛП. Признак оптимальности опорного решения в случае нахождения минимума целевой функции. Двойственность в линейном программировании. Целочисленное программирование: метод отсечения, метод ветвей и границ.

4 семестр

Раздел 8. Транспортная задача

Постановка транспортной задачи (ТЗ), ее математическая модель. Нахождение опорного плана методом «северо-западного угла» и методом распределения поставок с учетом наименьших затрат. Метод потенциалов.

Раздел 9. Матричные игры

Матричная игра как модель конфликтной ситуации. Основные понятия матричных игр. МИ двух игроков с нулевой суммой. Матричная игра двух лиц с седловой точкой. Нижняя и верхняя цена игры. Чистые и смешанные стратегии. Игры с природой (принятие решения в условиях риска и неопределенности). Математическое ожидание выигрыша. Критерии Лапласа, Вальда, Севиджа, Гурвица

Раздел 10. Теория массового обслуживания

Управляемый процесс в условиях неопределенности. Случайный процесс. Простейший поток случайных событий в системе массового обслуживания (СМО). Законы распределения вероятностей в простейшем потоке случайных событий в СМО. Математическая модель СМО. Понятие состояния СМО. Предельные вероятности состояний. Размеченный граф состояний СМО. Система дифференциальных уравнений Колмогорова для вероятностей состояний. Основные виды СМО: с отказами. СМО с ограниченной и неограниченной длиной очереди. Характеристики эффективности СМО. Замкнутые СМО. Характеристики эффективности.

СПИСОК ЛИТЕРАТУРЫ (основная и дополнительная)

Основная:

1. Акулич И.А. Математическое программирование в примерах и задачах. Высшая школа, 1993.

2. Гмурман В.Е. Теория вероятностей и математическая статистика. М., Высшая школа. 1979.

3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М., Высшая школа. 1979.

4. Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических вузов. Ч.1. - М.: Высшая школа, 1982 г.

5. Исследование операций в экономике. Под редакцией профессора Н.Ш. Кремера. М. «Банки и биржи». Издательское объединение «ЮНИТИ», 1997.

6. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М.: Наука, 1989 г.

7. Кузнецов А.В., Сакович В.А., Холод Н.И. Высшая математика. Математическое программирование. Минск.:Высшая школа, 1994.

8. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. М.: Высшая школа, 1980.

9. Маркович Э.С. Курс высшей математики с элементами теории вероятностей и математической статистики. - М.: Высшая школа, 1972 г.

10. Щипачев В.С. Высшая математика. - М.: Высшая школа, 1990 г.

11. Щипачев В.С. Сборник задач по высшей математике.- М.: Высшая школа, 1994 г.

Дополнительная:

12. Гавришина Л.Н. Предел. Дифференциальное исчисление. Часть 1. Кемеровский институт МГУК, 1997 г.

13. Гавришина Л.Н. Интегральное исчисление. Ряды. Часть 2. Кемеровский институт МГУК, 1997 г.

14. Гавришина Л.Н. Линейная алгебра. Часть 3. Кемеровский институт МГУК, 1998 г.

15. Гавришина Л.Н. Теория вероятностей. Случайные события. Часть 4. Кемеровский институт МГУК, 1999 г.

16. Гавришина Л.Н. Математика. Теория вероятностей. Пособие по решению задач. Кемеровский институт МГУК, 2001 г.

17. Гоголин В.А., Пинаев В.А. Прикладная математика. Кемеровский институт МГУК, 1999 г.

18. Курчин М.К. Теория вероятностей и математическая статистика. Конспект лекций №1. Кемеровский институт МГУК, 1997 г.

19. Курчин М.К. Теория вероятностей и математическая статистика. Конспект лекций №2. Кемеровский институт МГУК, 1997 г.

20. Курчин М.К. Начала линейной алгебры и аналитической геометрии. Кемеровский институт МГУК, 2001 г.

21. Курчин М.К. Дифференциальные уравнения. Кемеровский институт МГУК, 2000 г.

22. Курчин М.К. Ряды. Кемеровский институт МГУК, 2000 г.

23. Шуревич Г.И. Прикладная математика. Часть 1. Задача линейного программирования. Кемеровский институт МГУК, 1998 г.

24. Шуревич Г.И. Прикладная математика. Часть 2. Транспортная задача. Кемеровский институт МГУК, 1998 г.

25. Шуревич Г.И. Математика. Экономико-математические методы. Ч 1. Линейное программирование, 2001 г.

26. Шуревич Г.И. Математика. Экономико-математические методы. Ч 2. Транспортная задача, 2001 г.

КОНТРОЛЬНЫЕ ВОПРОСЫ ДЛЯ ЭКЗАМЕНА ЗА 1 КУРС

1. Определение функции. Область определения функции. Способы задания функции.

2. Определение предела функции.

3. Основные теоремы о пределах.

4. Первый и второй замечательные пределы.

5. Определение непрерывности функции. Свойства непрерывных функций.

6. Определение производной функции. Геометрический и физический смысл.

7. Основные правила дифференцирования.

8. Понятие дифференциала. Свойства дифференциала.

9. Правило Лопиталя.

10. Экстремумы функции. Необходимые и достаточные признаки существования экстремума.

11. Признаки постоянства, возрастания и убывания функции.

12. Общая схема построения графиков функций.

13. Понятие первообразной и неопределенного интеграла.

14. Свойства неопределенного интеграла.

15. Основные методы интегрирования.

16. Понятие определенного интеграла. Его свойства.

17. Геометрический смысл определенного интеграла.

18. Вычисление площади плоской фигуры.

19. Вычисление объема тела вращения.

20. Понятие о числовом ряде. Сходимость числового ряда.

21. Необходимый и достаточные признаки сходимости рядов.

22. Определение абсолютной и условной сходимости знакопеременного ряда.

23. Определение степенного ряда. Интервал сходимости.

24. Разложение функции в ряды Маклорена и Тейлора.

25. Различные виды уравнения прямой на плоскости.

26. Условия параллельности и перпендикулярности прямых.

27. Понятие определителя. Свойства определителей.

28. Способы вычисления определителей.

29. Понятие матрицы. Виды матриц.

30. Операции над матрицами.

31. Понятие обратной матрицы.

32. Система линейных уравнений.

33. Методы решения: Гаусса, Крамера, матричный.

34. Понятие случайного события. Классификация.

35. Алгебраические действия над событиями.

36. Определение вероятности события.

37. Основные формулы комбинаторики.

38. Теорема сложения вероятностей.

39. Вероятность полной группы событий.

40. Условная вероятность.

41. Теорема умножения вероятностей.

42. Независимые события. Теорема умножения для независимых событий.

43. Теорема сложения вероятностей двух совместных событий.

44. Формула полной вероятности.

45. Формулы Бейеса.

46. Формула Бернулли.

47. Локальная и интегральная теоремы Лапласа.

48. Теорема Пуассона.

ТЕМАТИКА КОНТРОЛЬНЫХ РАБОТ

Темы контрольной работы №1:

1. Предел функции.

2. Производная функции. Правила дифференцирования.

3. Исследование функций с помощью дифференциального исчисления.

4. Основные методы интегрирования.

5. Геометрическое приложение определенного интеграла.

6. Дифференциальные уравнения.

Темы контрольной работы №2:

Транспортная задача.

Игры с «природой».

КОНТРОЛЬНАЯ РАБОТА №1

ВАРИАНТ 0

1. Вычислить предел функции

а) 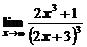;	б) ;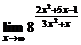
в) 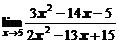;	г) ;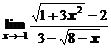

2. Вычислить производную функции

а) 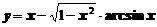;	б) ;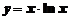

3. Исследовать функции 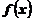и построить графики

, .

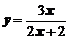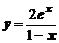4. Вычислить неопределенные интегралы

а) 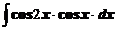;	б) ;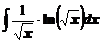
в) 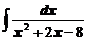;	г) .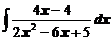

5. Найти общее решение дифференциального уравнения и построить графики двух различных частных решений этого уравнения

.

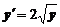ВАРИАНТ 1

1. Вычислить предел функции

а) 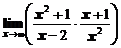;	б) ;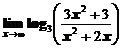
в) 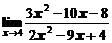;	г) ;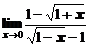

2. Вычислить производную функции

а) 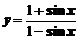;	б) ;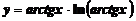

3. Исследовать функции 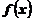и построить графики

, .

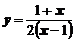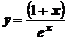4. Вычислить неопределенные интегралы

а) 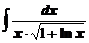;	б) ;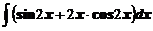
в) 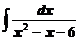;	г) .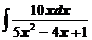

5. Найти общее решение дифференциального уравнения и построить графики двух различных частных решений этого уравнения

.

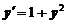ВАРИАНТ 2

1. Вычислить предел функции

а) 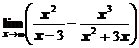;	б) ;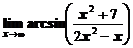
в) 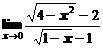;	г) ;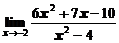

2. Вычислить производную функции

а) 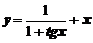;	б) ;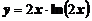

3. Исследовать функции 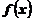и построить графики

, .

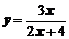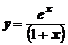4. Вычислить неопределенные интегралы

а) 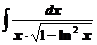;	б) ;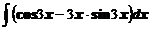
в) 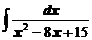;	г) .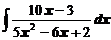

5. Найти общее решение дифференциального уравнения и построить графики двух различных частных решений этого уравнения

.

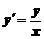ВАРИАНТ 3

1. Вычислить предел функции

а) 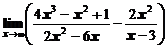;	б) ;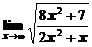
в) 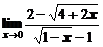;	г) ;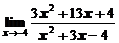

2. Вычислить производную функции

а) 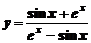;	б) ;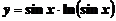

3. Исследовать функции 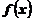и построить графики

, .

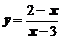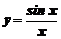4. Вычислить неопределенные интегралы

а) 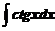;	б) ;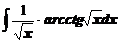
в) 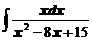;	г) .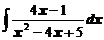

5. Найти общее решение дифференциального уравнения и построить графики двух различных частных решений этого уравнения

.

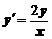ВАРИАНТ 4

1. Вычислить предел функции

а) 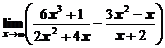;	б) ;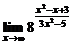
в) 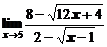;	г) ;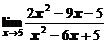

2. Вычислить производную функции

а) 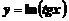;	б) ;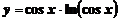

3. Исследовать функции 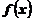и построить графики

, .

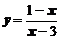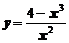4. Вычислить неопределенные интегралы

а) 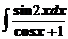;	б) ;
в) 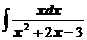;	г) .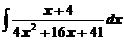

5. Найти общее решение дифференциального уравнения и построить графики двух различных частных решений этого уравнения

.

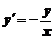ВАРИАНТ 5

1. Вычислить предел функции

а) 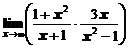;	б) ;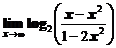
в) 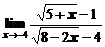;	г) ;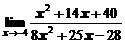

2. Вычислить производную функции

а) 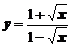;	б) ;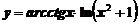

3. Исследовать функции 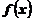и построить графики

, .

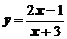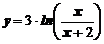4. Вычислить неопределенные интегралы

а) 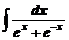;	б) ;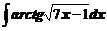
в) 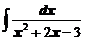;	г) .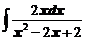

5. Найти общее решение дифференциального уравнения и построить графики двух различных частных решений этого уравнения

.

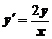ВАРИАНТ 6

1. Вычислить предел функции

а) 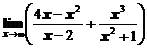;	б) ;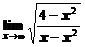
в) 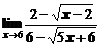;	г) ;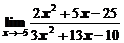

2. Вычислить производную функции

а) 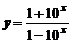;	б) ;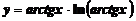

3. Исследовать функции 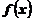и построить графики

, .

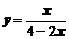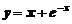4. Вычислить неопределенные интегралы

а) 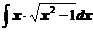;	б) ;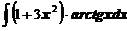
в) 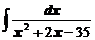;	г) .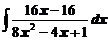

5. Найти общее решение дифференциального уравнения и построить графики двух различных частных решений этого уравнения

.

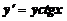ВАРИАНТ 7

1. Вычислить предел функции

а) 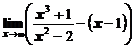;	б) ;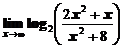
в) 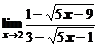;	г) ;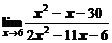

2. Вычислить производную функции

а) 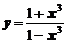;	б) ;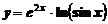

3. Исследовать функции 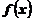и построить графики

, .

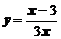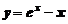4. Вычислить неопределенные интегралы

а) 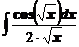;	б) ;
в) 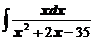;	г) .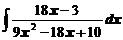

5. Найти общее решение дифференциального уравнения и построить графики двух различных частных решений этого уравнения

.

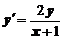ВАРИАНТ 8

1. Вычислить предел функции

а) 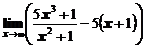;	б) ;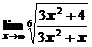
в) 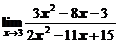;	г) ;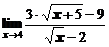

2. Вычислить производную функции

а) 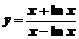;	б) ;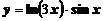

3. Исследовать функции 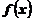и построить графики

, .

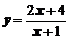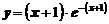4. Вычислить неопределенные интегралы

а) 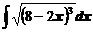;	б) ;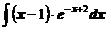
в) 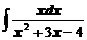;	г) .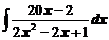

5. Найти общее решение дифференциального уравнения и построить графики двух различных частных решений этого уравнения

.

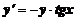ВАРИАНТ 9

1. Вычислить предел функции

а) 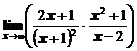;	б) ;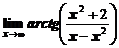
в) 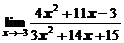;	г) ;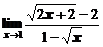

2. Вычислить производную функции

а) 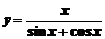;	б) ;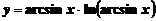

3. Исследовать функции 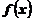и построить графики

, .

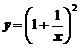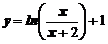4. Вычислить неопределенные интегралы

а) 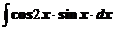;	б) ;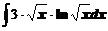
в) 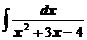;	г) .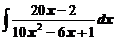

5. Найти общее решение дифференциального уравнения и построить графики двух различных частных решений этого уравнения

.

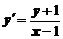МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Пример 4.

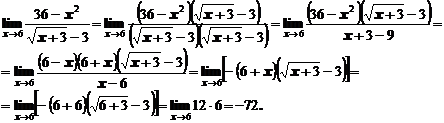
При вычислении пределов часто используются первый и второй замечательные пределы:

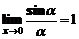
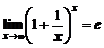и

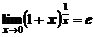
В последующем примере путем преобразования выражения выделяется первый замечательный предел.

Пример 5. При непосредственном вычислении получаем неопределенность вида .

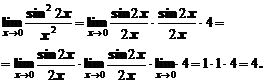
Пример 6. Вычислить предел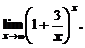

Здесь получается неопределенность вида 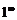. Для вычисления предела введем новую переменную 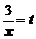. Отсюда 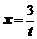, при 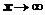, 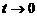. Итак, получим

.

Пример 7. Вычислить предел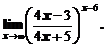

Сделаем простые преобразования для того, чтобы выделить целую часть дроби равную 1:

,

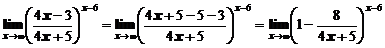Сделаем замену 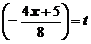, и преобразуем степень, чтобы получить второй замечательный предел

.

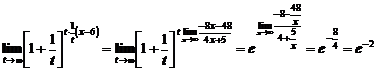Для раскрытия неопределенности вида или 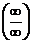также можно использовать правило Лопиталя, которое основано на следующей теореме.

Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных

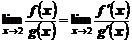
Заметим, что это правило можно применять несколько раз подряд.

Пример 8. Найти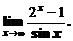

Здесь получается неопределенность вида . По правилу Лопиталя получим

Пример 9. Найти предел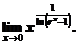

Представляя 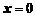, получим неопределенность вида 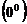. В подобных случаях можно использовать следующий прием.

Обозначим

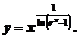
Прологарифмируем это выражение

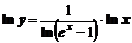
Найдем предел от обеих частей

Подставляя 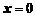, получим неопределенность вида 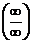. Применим правило Лопиталя:

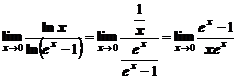
Подставляя 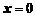, получим неопределенность вида . Применим еще раз правило Лопиталя:

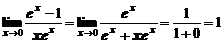
Теперь, учитывая, что функция 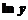непрерывна, поменяем местами операции:

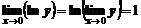
отсюда получим

Итак,

.

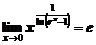II. При вычислении производных следует учитывать основные правила дифференцирования:

1. Постоянный множитель можно выносить за знак производной:

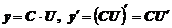(1)

2. Производная суммы (разности) функций равна сумме (разности) производных этих функций:

(2)

3. Производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:

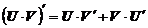(3)

Это правило справедливо для случая нескольких сомножителей.

4. Производная отношения двух функций равна дроби, в числителе которой разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а в знаменателе квадрат исходного знаменателя:

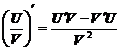(4)

5. Если 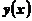сложная функция, т.е. 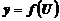, а ,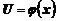

то производная 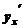находится, как 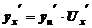(5)

Пример 10. Найти производную функции .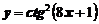

Обозначим 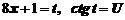, тогда получим .

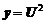Воспользуемся правилом 5 и таблицей производных (приложение 1).

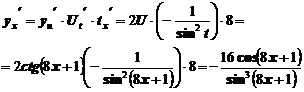
Пример 11. Найти производную функции .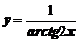

Рассматривая функцию как сложную и пользуясь правилом (4), получим

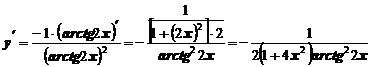
Пример 12. Найти производную функции .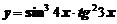

Рассматривая функцию как сложную и учитывая правило (3), получим

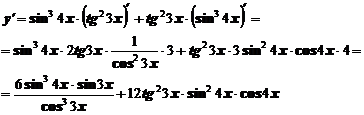
Иногда, чтобы облегчить нахождение производной логарифмической функции предварительно нужно сделать ее пр<