Показатели корреляции при нелинейных соотношениях рассматриваемых признаков. Смысл средней ошибки аппроксимации.

Индекс корреляции - нормированный показатель тесноты связи. Коэффициент индекса корреляции показывает долю общей вариации зависимой переменной, обусловленной регрессией или изменчивостью объясняющей переменной.Чем ближе индекс корреляции к 1 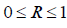, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии.

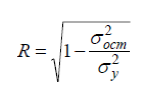
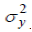общая дисперсия результативного признака y,

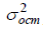остаточная дисперсия, определяемая по уравнению нелинейной регрессии.

Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии, т.е.уи ŷ. Чем меньше эти отличия, тем ближе теоретические значения к эмпирическим данным, тем лучше качество модели.

Ошибка аппроксимации - Величина отклонений фактических и расчетных значений результативного признака (у-ŷ_х) по каждому наблюдению. В отдельных случаях ошибка

аппроксимации может оказаться равной нулю. Отклонения (у–ŷ_х) несравнимы между собой, исключая величину, равную нулю.

Поскольку (у–ŷ_х) может быть величиной как положительной, так и отрицательной, ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.

Отклонения (у–ŷ_х) можно рассматривать:

- как абсолютную ошибку аппроксимации

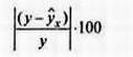
– как относительную ошибку аппроксимации. Для того чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, находят среднюю ошибку аппроксимации как среднюю арифметическую простую.

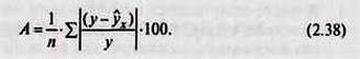
Назначение частной корреляции при построении модели множе-ственной регрессии.

Ранжирование факторов, участвующих во множественной

линейной регрессии, может быть проведено через стандартизованные коэффициенты

регрессии, с помощью частных коэффициентов корреляции — для линейных связей.

Кроме того, частные показатели корреляции широкоиспользуются при решении проблемы отбора факторов: целесообразность включениятого или иного фактора в модель доказывается величиной показателя частнойкорреляции.

Частные коэффициенты корреляции характеризуют тесноту

связи между результатом и соответствующим фактором при устранении влияния

других факторов, включенных в уравнение регрессии.

Показатели частной корреляции - отношение сокращения

остаточной дисперсии за счет дополнительного включения в анализ нового

фактора к остаточной дисперсии, имевшей место до введения его в модель.

Частные коэффициенты корреляции измеряющие влияние на у фактора х_i

при неизменном уровне др. факторов можно определить по формуле:

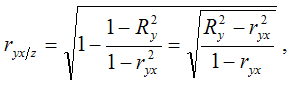
где 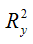– множественный коэффициент детерминации двухфакторной модели регрессии;

При двух факторах и i=1 данная формула примет вид:

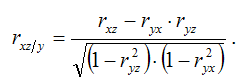
Частные коэффициенты корреляции изменяются в пределах от -1 до 1.