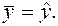Статистический смысл коэффициента детерминации. Какова связь между линейным коэффициентом корреляции и коэффициентом регрессии в линейной модели парной регрессии?
коэффициент детерминациирассчитывается как квадрат линейного коэффициента корреляции r 2 . Он характеризует долю дисперсии результативного признака y , объясняемую регрессией, в общей дисперсии результативного признака:
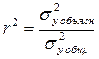
Величина коэффициента детерминации служит одним из критериев оценки качества линейной модели. Чем больше доля объясненной вариации, тем соответственно меньше роль прочих факторов, и , следовательно, линейная модель хорошо аппроксимирует исходные данные и ею можно воспользоваться для прогноза значений результативного признака
При линейной регрессии в качестве показателя тесноты связи выступает линейный коэффициент корреляции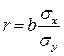 
. Коэффициент регрессии показывает, на сколько единиц в среднем изменится У, когда Х увеличивается на одну единицу. Однако он зависит от единиц измерения переменных. Как показателя тесноты связи нужна такая стандартная система единиц измерения, в которой данные по различным характеристикам оказались бы сравнимы между собой.
Типы моделей нестационарных временных рядов.
Стохастический процесс - процесс, который развивается во времени в соответствии с законами теории вероятностей.
К стохастическим процессам относится:
· Стохастический процесс называется стационарным, если его основные свойства остаются неизменными во времени.
· Нестационарным временным рядом называется ряд, который не удовлетворяет вышеперечисленным свойствам.
Для описания временных рядов, нестационарных по среднему значению, используются два основных класса моделей:
• модели временных рядов с детерминированным трендом, т.е. модели с трендом в виде детерминированной функции времени;
• модели интегрированных временных рядов, которые в общем случае представляются в виде модели авторегрессии интегрированного скользящего среднего
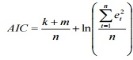
Выбор следует сделать в пользу модели с меньшим значением AIC.
Критерий Шварца
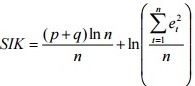
Баланс для сумм квадратов отклонений результативного признака. В каком случае общая СКО равна факторной? Что происходит, когда общая СКО равна остаточной?
Баланс для сумм квадратов отклонений результативного признака.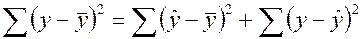 
или Q = Qr + Qe, где Q – общая сумма квадратов отклонений зависимой переменной от средней, Qr и Qe – соответственно, сумма квадратов, обусловленная регрессией, и остаточная сумма квадратов, характеризующая влияние неучтённых факторов.
Общая СКО равна факторной, когда прочие факторы не влияют на результат, y связан с x функционально, и остаточная СКО равна нулю.
Когда общая СКО в точности равна остаточной, сумма квадратов, обусловленная регрессией равняется нулю. Фактор х не оказывает влияния на результат, вся дисперсия y обусловлена воздействием прочих факторов, линия регрессии параллельна оси Ох и 