Типы моделей и переменных, применяемых в эконометрике. Чем регрессионная модель отличается от функции регрессии?

Для моделирования эконометрических взаимосвязей между экономическими явлениями чаще всего применяется три типа моделей и три типа переменных.

Типы моделей:

1) Модели временных рядов - Модель представляет собой зависимость результативного признака от переменной времени или переменных, относящихся к другим моментам времени.

2) Модели регрессии - это уравнение, в котором объясняемая переменная представляется в виде функции от объясняющих переменных (например, модель спроса на некоторый товар в зависимости от его цены и дохода покупателей).

3) Системы одновременных уравнений - системы уравнений, состоящие из регрессионных уравнений и тождеств, в каждом из которых помимо объясняющих – независимых – переменных содержатся объясняемые переменные из других уравнений системы.

Типы переменных:

1)Экзогенные (внешние, независимые)- это внешние для модели переменные, управляемые из вне, влияющие на эндогенные переменные, но не зависящие от них. Х-обознач.

2)Эндогенные(внутренние, зависимые)- это внутренние, формируемые в модели переменные, зависимые от предопределенных переменных. Y-обоз.

3)Предопределенные (экзогенные и лаговые эндогенные)-называют экзогенные переменные х и лаговые эндогенные переменные yt-l.

Регрессионная модель – это уравнение, в котором объясняемая переменная представляется в виде функции от объясняющих переменных.

Функция регрессии –функция f(x1,x2..)описывает зависимость условного среднего значения результативной переменной y от заданных объясняющих переменных.

Этапы эконометрического моделирования. Каковы основные причины наличия в регрессионной модели случайного отклонения?

Этапы эконометрического моделирования:

1. постановочный – определение целей и задач модели;

2. априорный – предварительный анализ ситуации;

3. спецификация модели – выбор типа модели, состава переменных и формы математической связи между ними;

4. информационный – сбор необходимой статистической информации, т.е. регистрации значений показателей, участвующих в описании модели;

5. идентификация модели – оценивание неизвестных значений параметров модели по имеющимся исходным статистическим данным;

6. верификация модели– проверка качества модели в целом и ее параметров;

7. интерпретация результатов – формулирование выводов и рекомендаций на основе построенной модели.

Типы моделей и переменных, применяемых в эконометрике. Чем регрессионная модель отличается от функции регрессии? - student2.ru

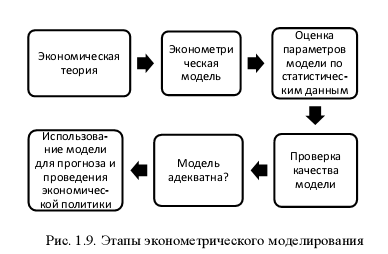
Известно, что основной причиной наличия случайного отклонения в регрессионной модели являются несовершенные знания о причинах и взаимосвязях, определяющих то или иное значение выходной переменной. Поэтому свойства случайных отклонений, в первую очередь зависит от выбора вида функции отклика и состава входных переменных (факторов).

ARIMA-модель.

Для описания нестационарных однородных временных рядов применяется модель Бокса-Дженкинса (ARIMA –модель).

Этапы методологии Бокса-Дженкинса:

1. Тестирование исходного ряда на стационарность. Анализ автокорреляционной функции. Переход к стационарному ряду путем взятия последовательных разностей (дискретные производные). Определение параметра q.

2. Исследование характера автокорреляционной функции и предположение о значениях параметров k (порядок авторегрессии) и m (порядок скользящего среднего).

3. Оценивание параметров ARIMA (k,m,q) – модели.

4. Проверка пробной модели на адекватность путем анализа ряда остатков.

Для обнаружения «белого шума» в остатках применяют Q-статистику

Бокса-Пирса, H₀ об отсутствии автокорреляции в остатках:

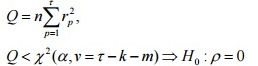
Критерии качества подгонки модели Бокса-Дженкинса:

Критерий Акайка

Основные понятия и характеристики панельных данных.

Панельные данные - Множество данных, состоящих из наблюдений за однотипными статистическими объектами, в течение нескольких временных периодов. Когда периодов времени больше числа наблюдаемых объектов, панельные данные называют также объединенным временным рядом.

Сущность панельных данных заключается в наличии множественных наблюдений за одними и теми же объектами. Любое множество панельных данных имеет ряд общих характеристик. Тем не менее в зависимости от фактического процесса, генерирующего данные, для каждого множества панельных данных появляются свои особые свойства.

Свойства панельных данных:

- позволяют учесть в модели ненаблюдаемую гетерогенность;

- позволяют идентифицировать потоки или перемещения между различными состояниями наблюдаемых объектов.

Сбалансированной панелью называют панельные данные, в которых нет пропущенных наблюдений. Сокращение объектов в выборке называют панельным истощением. Ротационной панелью называют панельные данные, в которых в обследуемую выборку периодически добавляется новый объект.

В микроэконометрических панелях объекты наблюдения – индивиды, домохозяйства, предприятия.

В макроэконометрических панелях объектами наблюдения служат страны, регионы, города.

Предположения простейших моделей панельных данных:

- Статические модели, без лаговых значений зависимых переменных;

-Сбалансированные панели с одинаковым числом временных тактов;

-Панели с короткими временными рядами;

- Включение аддитивных фиктивных переменных для отражениявременного эффекта;

-Учет ненаблюдаемых и неизменяемых во времени характеристик объек-тов выборки – индивидуального эффекта.

Типы моделей:

Типы переменных: