Классическая формула вычисления вероятности

Вопросы

1. Классическая формула вычисления вероятности.

2. Геометрическая вероятность.

3. Статистическое определение вероятности и его применение.

4. Теоремы сложения и умножения.

5. Формулы полной вероятности и Байеса.

6. Повторение опытов. Формула Бернулли. Мода биноминального распределения.

7. Повторение опытов (при большом n). Формула Пуассона.

8. Повторение опытов (при большом n). Теорема Муавра-Лапласа.

9. Повторение опытов (при большом n). Интегральная теорема Муавра-Лапласа.

10. Дискретная случайная величина. Способы задания.

11. Биномиальное распределение и его характеристики.

12. Распределение Пуассона и его характеристики.

13. Геометрическое распределение и его характеристики.

14. Гипергеометрическое распределение.

15. Математическое ожидание и его свойства.

16. Вероятностный смысл математического ожидания.

17. Дисперсия, ее свойства, вероятностный смысл.

18. Непрерывная случайная величина. Способы её задания.

19. Функция распределения дискретной и непрерывной случайной величины и ее свойства.

20. Плотность распределения и ее свойства.

21. Нормальное распределение. Стандартное нормальное распределение и его свойства.

1. Числовые характеристики случайной величины, начальные, центральные и эмпирические моменты. Являются ли они случайными величинами?
2. Нормальное распределение, нормальная кривая, его мода и медиана, асимметрия и эксцесс.

24. Математическое ожидание и дисперсия непрерывной случайной величины.

25. Равномерное непрерывное распределение и его свойства.

26. Закон больших чисел.

27. Центральная предельная теорема.

28. Система двух дискретных случайных величин и ее характеристики.

29. Система двух непрерывных случайных величин и ее характеристики.

30. Теорема о необходимом и достаточном условии независимости компонент двух мерной случайной величины.

31. Плотности компонент двух мерной случайной величины и условные вероятности.

32. Условные математические ожидания, линия регрессии.

33. Корреляционный момент, коэффициент корреляции. Коррелированность и независимость компонент.

34. Функции одной случайной величины, дискретной и непрерывной. Закон распределения и числовые характеристики.

35. Статистическое распределение выборки, эмпирическая функция распределения, полигон и гистограмма.

36. Точечные оценки. Основные определения. Несмещённость, эффективность и состоятель­ность.

37. Метод наименьших квадратов для определения линии линейной регрессии, эмпирический коэффициент корреляции.

38. Метод произведений для вычисления эмпирического коэффициента корреляйции.

39. Метод моментов. Условные варианты и метод произведений для определения математического ожидания, дисперсии, асимметрии и эксцесса

40. Метод наибольшего правдоподобия.

41. Интервальные оценки параметров распределений.

42. Проверка статистических гипотез. Основные определения.

43. Проверка гипотез о числовых характеристиках генеральной совокупности.

44. Критерии согласия Пирсона.

Задачи

КЛАССИЧЕСКАЯ ФОРМУЛА ВЫЧИСЛЕНИЯ ВЕРОЯТНОСТИ

N1.

Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.

N2.

В партии из N деталей имеется n стандартных. Наудачу отобраны m деталей. Найти' вероятность того, что среди отобранных деталей ровно k стандартных.

N3.

В цехе работают 6 мужчин и 4 женщины. По табельным номерам наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных лиц окажутся 3 женщины.

N4.

На складе имеется 15 кинескопов, причем 10 из них изготовлены Львовским заводом. Найти вероятность того, что среди наудачу взятых пяти кинескопов окажутся 3 кинескопа Львовского завода.

N5.

В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов окажутся 5 отличников.

N6.

В коробке имеется 5 одинаковых изделий, причем 3 из них окрашены. Наудачу извлечены 2 изделия. Найти вероятность того, что среди извлеченных двух изделий окажутся: а) одно окрашенное изделие; б) два окрашенных изделия.

N7.

В коробке имеется 5 одинаковых изделий, причем 3 из них окрашены. Наудачу извлечены 2 изделия. Найти вероятность того, что среди извлеченных двух изделий окажется хотя бы одно окрашенное изделие.

N8.

"Секретный" замок содержит на общей оси 4 диска, каждый из которых разделен на 5 секторов с различными написанными на них цифрами. Замок открывается только в том случае, если диски установлены так, что цифры дисков образуют определенное четырехзначное число. Найти вероятность того, что при произвольной установке дисков замок можно будет открыть.

N9.

Отдел технического контроля обнаружил 5 бракованных книг из 50 просмотренных в партии из 100 книг. Найти вероятность обнаружить оставшиеся бракованные при просмотре еще 10 книг, если всего в партии 7 бракованных.

N10.

В партии из 10 приборов 1 негодный. Взяли 2 прибора. Найти вероятность того, что неисправный не попался.

ГЕОМЕТРИЧЕСКАЯ ВЕРОЯТНОСТЬ.

N11.

К автобусной остановке через каждые 4 минуты подходит автобус линии А и через каждые 6 минут - автобус линии В. Определить вероятность того, что первый подошедший автобус окажется автобусом линии А.

N12.

Два лица имеют одинаковую вероятность прийти к указанному месту в любой момент промежутка времени Т. Определить вероятность того, что время ожидания одним другого будет не больше t.

N13.

Какова вероятность того, что случайно выбранная на глобусе точка лежит за полярным кругом (66 градусов 33 минуты северной широты)?

N14.

Какова вероятность, не целясь, попасть бесконечно малой пулей в прутья квадратной решетки, если толщина прутьев равна а, а расстояние между их осями равно L (L>a).

N15.

На перекрестке установлен автоматический светофор, в котором 1 минуту горит зеленый свет и 0.5 минуты - красный, затем снова 1 минуту - зеленый и 0.5 минуты - красный,... . Какова вероятность для случайно подъехавшего автомобиля проехать перекресток без остановки?

N16.

Луч локатора перемещается в горизонтальной плоскости с постоянной угловой скоростью. Какова вероятность того, что цель будет обнаружена в угловом секторе А радиан, если появление цели по любому направлению равновозможно?)

N17.

Какова вероятность того, что сумма двух наудачу взятых отрезков , длина каждого из которых не превосходит L, будет больше L?

N18.

На шарик нанесена сетка географических координат. Шарик брошен на плоскость. Какова вероятность того, что шарик прикоснется к плоскости точкой, которая находится в области между 0 и 90-м градусами восточной долготы?

N 19.

Какова вероятность того, что шарик прикоснется к плоскости точкой, которая находится в области между45 и 90-м градусами северной широты? (см. условие предыдущей задачи).

N20.

В случайный момент времени х є [0,Т] появляется радиосигнал длительностью Т1. В случайный момент времени Y є [0, Т] включается приемник на время Т2<Т1. Найти вероятность обнаружения сигнала, если время настройки приемника равно Т3 (Т3<Т2<Т1).

N21.

Вероятность того, что при одном выстреле стрелок попадет в десятку, равна 0.6. Сколько выстрелов должен сделать стрелок, чтобы с вероятностью не менее 0.8 он попал десятку хотя бы один раз?

N22.

Три электрические лампочки последовательно включены в цепь. Вероятность того, что одна лампочка перегорит, если напряжение в сети превысит номинальное, равна 0.6. Найти вероятность того, что при повышенном напряжении тока в цепи не будет.

N23.

Вероятность того, что событие А появится хотя бы один раз при двух независимых испытаниях, равна 0.75. Найти вероятность появления события в одном испытании.

N24.

Три команды Al, A2, A3 спортивного общества А состязаются соответственно с тремя командами общества В. Вероятности того, что команды общества А выиграют матчи у команд общества В таковы: при встрече A1 с В1 - 0.8; A2 с В2 - 0.4; A3 с ВЗ - 0.4. Для победы необходимо выиграть не менее двух матчей из трех. Победа какого из общества вероятнее?

N25.

Вероятность поражения цели первым стрелком при одном выстреле равна 0.8, а вторым стрелком - 0.6. Найти вероятность того, что цель будет поражена только одним стрелком.

N26.

Из последовательности чисел 1, 2,... , n наудачу одно за другим выбираются два числа. Найти вероятность того, что одно из них меньше заданного целого положительного числа k, а другое больше k, где 1 < k < n.

N27.

Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие нестандартно, равна 0.1. Найти вероятность того, что из трех проверенных изделий только одно окажется нестандартным.

N28.

Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие нестандартно, равна 0.1. Найти

вероятность того, что нестандартным окажется только четвертое по порядку проверенное изделие.

N29.

Гардеробщица выдала одновременно номерки трем лицам, сдавшим в гардероб свои шляпы. После этого она перепутала все шляпы и повесила их наугад. Найти вероятность следующих событий:

А = {каждому из трех лиц гардеробщица выдаст его собственную шляпу};

С = {ровно два лица получат свои шляпы}.

N30.

Гардеробщица выдала одновременно номерки трем лицам, сдавшим в гардероб свои шляпы. После этого она перепутала все шляпы и повесила их наугад. Найти вероятность следующих событий:

D = {ровно одно лицо получит свою шляпу};

Е = {ни одно из трех лиц не получит своей шляпы}.

N31.

Прибор состоит из двух узлов; работа каждого узла безусловно необходима для работы прибора в целом. Надежность (вероятность безотказной работы в течение времени t) первого узла равна р1, второго р2. Прибор испытывался в течение времени t, в результате чего обнаружено, что он вышел из строя (отказал). Найти вероятность того, что отказал только первый узел, а второй исправен.

N32.

Рассматривается посадка самолета на аэродром. Если позволяет погода, летчик сажает самолет, наблюдая за аэродромом визуально. В этом случае вероятность благополучной посадки равна р1. Если аэродром затянут низкой облачностью, летчик сажает самолет вслепую по приборам. Надежность (вероятность безотказной работы) приборов слепой посадки равна Р. Если приборы слепой посадки сработали нормально, то самолет садится благополучно с той же вероятностью р1, что и при визуальной посадке. Если же приборы слепой посадки не сработали, то летчик может благополучно посадить самолет только с очень малой вероятностью р*. Известно, что при плохой видимости самолет приземлился благополучно. Найти вероятность того, что посадка произошла по приборам слепой посадки.

N33.

У рыбака имеется три излюбленных места для ловли рыбы, которые он посещает с равной вероятностью каждое. Если он закидывает удочку на первом месте, рыба клюет с вероятностью р1; на втором месте - с вероятностью р2; на третьем - с вероятностью р3. Известно, что рыбак, выйдя на ловлю рыбы, три раза закинул удочку и рыба клюнула только один раз. Найти вероятность того, что он удил рыбу на первом месте.

N34,35.

Завод изготовляет изделия, каждое из которых с вероятностью р имеет дефект. В цехе изделие с равной вероятностью осматривается одним из двух контролеров. Первый контролер обнаруживает имеющийся дефект с вероятностью р1, второй - с вероятностью р2. Если изделие не было забраковано в цехе, то оно попадает в ОТК завода, где дефект, если он имеется, обнаруживается с вероятностью р0. Известно, что изделие забраковано. Найти вероятность того, что оно забраковано:

(34) А - первым контролером;

В - вторым контролером;

(35) С - ОТК завода.

N36.

В группе из 10 студентов, пришедших на экзамен, 3 подготовленных отлично, 4 - хорошо, 2 - посредственно и 1 - плохо. В экзаменационных билетах имеется 20 вопросов. Отлично подготовленный студент может ответить на все 20 вопросов, хорошо подготовленный - на 16, посредственно - на 10, плохо - на 5. Вызванный наугад студент ответил на три произвольно заданных вопроса. Найти вероятность того, что этот студент подготовлен: а) отлично; б) плохо.

N37.

На вход радиолокационного устройства с вероятностью р поступает смесь полезного сигнала с помехой, а с вероятностью (1-р) - только одна помеха. Если поступает полезный сигнал с помехой, то устройство регистрирует наличие сигнала с вероятностью р1; если только помеха - с вероятностью р2 (ложная регистрация несуществующего сигнала). Известно, что устройство зарегистрировало наличие какого-то сигнала. Найти вероятность того, что в его составе имеется полезный сигнал.

N38.

Пассажир может обратиться за получением билета в одну из трех касс. Вероятности обращения в каждую кассу зависят от их местоположения и равны соответственно р1,р2,р3. Вероятность того, что к моменту прихода пассажира имеющиеся в кассе билеты будут распроданы, равна для первой кассы Р1, для второй Р2, для третьей РЗ. Пассажир направился за билетом в одну из касс и приобрел билет. Найти вероятность того, что это была первая касса.

N39.

Производится один выстрел по плоскости, на которой расположены две цели: I и II. Вероятность попадания в цель I равна р1, в цель II равна р2. После выстрела получено известие, что попадания в цель I не произошло. Какова теперь вероятность того, что произошло попадание в цель II?

N40.

Имеются две урны: в первой а белых шаров и b черных; во второй с белых и d черных. Выбирается наугад одна из урн и вынимается из нее один шар. Этот шар оказался белым. Найти вероятность того, что следующий шар, который мы вынем из той же урны, будет тоже белым.

N41.

Предположим, что кость имеет s граней s>=2, выпадение каждой из которых одинаково вероятно. Через g(t,n) обозначим вероятность того, что при t бросаниях кости заданная грань выпадет меньше, чем n раз. Найти g(t,n).

N42.

Среди коконов некоторой партии 30% цветных. Какова вероятность того, что среди 10 случайно выбранных из партии 3 цветных? Не более 3 цветных?

N43.

Технический контроль проверяет изделия, каждое из которых независимо от других изделий может с вероятностью Р оказаться дефектным. Какова вероятность того, что из 10 проверенных изделий только одно оказалось дефектным?

N44.

Вероятность того, что замаскировавшийся противник находится на обстреливаемом участке, равна 0,3; вероятность попадания при каждом отдельном выстреле равна 0.2. Для поражения достаточно одного попадания. Какова вероятность поражения при 2 выстрелах? При 10 выстрелах?

N45.

Спортивные общества А и В состязаются тремя командами. Вероятности выиграша матчей команд общества А против соответствующих команд В можно принять соответственно равными 0.7 для 1-ой (против 1-ой В), 0.6 для 2-ой (против 2-ой В), 0.2 для 3-тей(против 3-тей В). Для победы необходимо выиграть не менее 2-х матчей из трех (ничьих не бывает). Чья победа вероятнее?

N46.

Два равных по силам шахматиста А и В согласились сыграть матч на следующих условиях: выигрывает тот, кто одержал не менее 5 побед, но не более 2 проигрышей. Найти вероятность того, что кто-нибудь победит.

N47.

Рабочий обслуживает 12 однотипных станков. Вероятность того, что станок потребует к себе внимания рабочего в течение промежутка времени длительности Т равна 1:3. Чему равна вероятность того, что за время Т а)4 станка потребуют к себе внимание рабочего;

б)число требований к рабочему со стороны станков за время Т будет между 3 и 6.

N48.

В семье 4 человека. Считая вероятность рождения в течение каждого из месяцев для каждого лица равной 1/12, найти вероятность того, что 3 лица родились в январе, а 4-тое в октябре.

N49.

Известно, что вероятность выпуска бракованного сверла равна 0.02. Сверла укладываются в коробки по 10 штук. Чему равна вероятность того, что в коробке не окажется бракованных сверл;

число бракованных сверл окажется не более З?

N50.

Известно, что вероятность выпуска бракованного сверла равна 0.02. Сверла укладываются в коробки. Сколько нужно класть в коробку сверл, чтобы с вероятностью, не меньшей 0.99, в ней было не менее 10 исправных?

N51.

При испытании легированной стали на содержание углерода вероятность того, что в случайно взятой пробе процент углерода превысит допустимый уровень, равна Р=0.01. Считая применимым закон редких явлений, вычислить, сколько в среднем необходимо испытать образцов, чтобы с вероятностью Р=0.95 указанный эффект наблюдался по крайней мере 1 раз.

N52.

Учебник издан тиражом 100 000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0.0001. Найти вероятность того, что тираж содержит ровно 5 бракованных книг;

не менее 5 бракованных книг.

N53.

Устройство состоит из 1000 элементов, работающих независимо. Вероятность выхода любого из них в течение времени Т равна 0.002. Найти вероятность того за время Т откажут ровно 3 элемента; не более 5 элементов.

N54.

Коммутатор учреждения обслуживает 100 абонентов. Вероятность того, что в течение одной минуты абонент позвонит на коммутатор, равна 0.01. Найти вероятность того, что в течение одной минуты позвонят ровно 3 абонента; менее 3 абонентов; более 3 абонентов;

хотя бы 1 абонент.

N55.

Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение одной минуты равна 0.003. Найти вероятность того, что в течение одной минуты произойдет ровно 2 обрыва нити; менее 2 обрывов; хотя бы 1 обрыв.

N56.

Устройство состоит из большого числа элементов, работающих независимо; вероятность выхода из строя любого из них в течение времени Т одинакова и очень мала. Найти среднее число элементов, отказавших за время Т, если вероятность отказа хотя бы одного за это время 0.98.

N57.

Вероятность брака для 1 изделия очень мала. Найти среднее число бракованных изделий в большой партии изделий, если вероятность того, что в этой партии содержится хотя бы одно бракованное изделие, равна 0.95.

N58.

Вероятность появления события А в одном опыте очень мала и равна Р. Доказать, что сумма вероятностей числа появлений события А при бесчисленном количестве независимых испытаниях

равна 1.

N59.

Вероятность попадания в цель при одном выстреле равна 0.01. Найти вероятность того, что при 100 выстрелах будет не больше 3 попаданий.

N60.

На одной странице 2000 знаков. При типографском наборе вероятность искажения одного знака равна 1/800. Найти вероятность того, что на странице не менее 2 опечаток.

N61.

Имеется n-лампочек; каждая из них с вероятностью р имеет дефект. Лампочка ввинчивается в патрон и включается ток; при включении тока дефектная лампочка сразу же перегорает, после чего заменяется другой. Е - случайная величина числа лампочек, которое будет испробовано.

N62.

Два баскетболиста поочередно забрасывают мяч в корзину до тех пор, пока один из них не попадет. Е - случайное число бросков, производимых каждым из баскетболистов, если вероятность попадания первого равна 0.4, а второго0.6.

N63.

Мишень состоит из круга 1 и двух концентрических колец с номерами 2 и 3. Попадание в круг 1 дает 10 очков, в кольцо 2 дает 5 очков, а в кольцо 3 - 1 очко. Вероятности попадания в круг 1 и в кольца 2 и 3 соответственно равны 0.5, 0.3, 0.2. Е - случайная сумма выбитых очков в результате трех выстрелов.

N64.

Производятся испытания n изделий на надежность, причем вероятность выдержать испытание для каждого изделия равна р. Е -случайное число изделий, выдержавших испытание.

N65.

Имеется n заготовок для одной и той же детали. Вероятность изготовления годной детали из каждой заготовки равна р. Е -случайное число используемых заготовок.

N66.

В партии из 10 деталей содержится 3 нестандартных. Наудачу отобраны 2 детали. Е - число нестандартных деталей среди 2 отобранных.

N67.

Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна0.9. В каждой партии содержится 5 изделий. Е - число партий, в каждой из

которых окажется ровно 4 стандартных изделия, если проверке подлежат 50 партий.

N68.

Имеется 6 ключей, из которых только один подходит к замку. Е -число попыток при открывании замка, если испробованный ключ в последующих открываниях не участвует.

N69.

Батарея состоит из 3-х орудий. Вероятность попадания в цель при одном выстреле из первого, второго и третьего орудия батареи равна соответственно: 0.5, 0.6 и 0.8. каждое из орудий стреляет по некоторой цели один раз. Е - число попаданий в мишень.

N70.

Производится набрасывание колец на колышек до первого попадания (либо до полного израсходования колец). Число колец равно пяти. Е - число брошенных колец, если вероятность попадания 0.9.

N71.

х + а, х є (0;1);

f(x)= 0, иначе, а - ?

N72.

ax², 0<=x<=l;

f(x)= 0, иначе, а -?

N73.

a cos х, 0 < x < П/2;

f(x)= 0, иначе, а- ?

N74.

(sin x )/ a, x є (0; П);

f(x)= 0, иначе, а- ?

N75.

2a - 3x, 0 <=x<5;

f(x)= 0, иначе, а - ?

N76.

(a cos² x)/3, x е (-П/2;П/2);

f(x)= 0, иначе, а -?

N77.

b x² , x є (0;3);

f(x)= 0, иначе, b- ?

N78.

с х³, х є (0;1);

f(x)= 0, иначе, с - ?

N79.

x² + ax, x є (0;1);

f(x)= 0, иначе, а - ?

N80.

x² + a, x є (0;2);

f(x)= 0, иначе, а - ?

НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ.

N81.

Автомат штампует детали. Контролируется длина детали X, которая распределена нормально с математическим ожиданием (проектная длина) 50 мм. Фактически, длина изготовленных деталей не менее 32мм и не более 68 мм. Найти вероятность того, что длина случайно отобранной детали будет меньше 40 мм; больше 55 мм.

N82.

Производится измерение диаметра вала без систематических (одного знака) ошибок. Случайные ошибки измерения подчинены нормальному закону со средним квадратическим отклонением 8=10мм. Найти вероятность того, что при двух измерениях ошибка ни в одном не превзойдет15 мм.

N83.

Случайная величина Х имеет нормальное распределение с математическим ожиданием М=25. Вероятность попадания Х в интервал(10,15) равна 0.2. Чему равна вероятность попадания Х в интервал(35,40)?

N84.

Случайные ошибки измерения подчинены нормальному закону с математическим ожиданием 0 и средним квадратичным отклонением 10 мм. Найти вероятность того, что при3-х независимых измерениях ошибка хотя бы одного не превзойдет 10 мм?

N85.

Случайная величина Х имеет нормальное распределение с математическим ожиданием М=10. Вероятность попадания Х в интервал (0,20) равна 0.9973. Чему равна вероятность попадания Х в интервал (0,5)?

N86.

Случайная величина Х имеет нормальное распределение N(0,1). Что больше: вероятность попадания Х в интервал (-0.5,-0.1) или в интервал (1,2)?

N87.

Случайная величина Х имеет нормальное распределение N(0,1). Что больше: вероятность /Х/>0.7 или /Х/<0.3?

N88.

Случайная величина Х имеет нормальное распределение N(1,1). Что больше: вероятность попадания Х в интервал (-1,0) или в интервал (0,0.5)?

N89.

Случайная величина Х имеет нормальное распределение с математическим ожиданием М=0. Вероятность попадания Х в интервал (0,2) равна 0.9. Чему равна вероятность попадания Х в

интервал (0,1)?

N90.

В нормально распределенной совокупности 25% значений Х меньше 0 и 40% значений Х больше 2. Найти среднее значение и стандартное отклонение данного распределения.

Задание№4

В вариантах № 1 – 30 приведены результаты n = 50 наблюдений за парой признаков (X, Y). В задании необходимо выполнить в 1-ую очередь задачи № 1 – 5 и 9 – 11; затем три оставшихся, то есть № 6 – 8.

1. Составить корреляционную Таблицу, содержащую два входа, по числу признаков, пояснить ее устройство;

2. Построить вариационный ряд для признака X или Y (задано в данных варианта);

3. Найти числовые характеристики заданого признака (X или Y): методом произведений вычислить выборочное среднее, выборочную дисперсию, D_в, выборочное среднее квадратическое отклонение 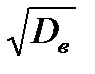, и определить для выбранного признака исправленную дисперсию, S², и “исправленное” среднее квадратическое отклонение 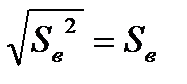, существенна ли поправка?

4. Найти другие характеристики вариационного ряда для признака X или Y: Моду М_о, Медиану m_e, Размах варьирования R, Среднее абсолютное отклонение θ, Коэффициент вариации V.

5. Построить полигон частот и найти эмпирическую функцию распределения для заданого признака (X или Y);

6. Предполагая, что заданый признак (X или Y) распределен в генеральной совокупности по нормальному закону, найти с надежностью γ (γ – задано) доверительный интервал для оценки неизвестного математического ожидания а в генеральной сово­купности при неизвестном σ (среднем квадратическом отклонении);

7. Предполагая, что заданый признак (X или Y) распределен в генеральной совокупности по нормальному закону, найти с надежностью γ (γ – задано) доверительный интервал для оценки среднего квадратического отклонения σ;

8. Найти методом наибольшего правдоподобия оценки параметров а и σ для нормально распределенного заданного признака, является ли оценка для σ несмещенной?

9. Найти выборочный коэффициент корреляции между признаками Y и X;

10. Найти уравнение линейной регрессии 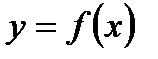и дать объяснение полученного результата, объяснить смысл найденного коэффициента корреляции;

11.Построить корреляционное поле по корреляционной Таблице и нанести график найденной прямой регрессии на корреляционное поле, нанести на этот же график соответствующие условные вероятности.

Контрольные вопросы:

· Какие задачи решает математическая статистика?

· Дайте определение генеральной и выборочной совокупностей, варианты, вариационного ряда, статистического распределения для выборки и эмпирической функции распределения;

· Что мы понимаем под репрезентативностью, эффективностью и состоятельностью выборки?

· Что значит несмещенность выборочной средней и смещенность выборочной дисперсии?

· В чем отличие интервальных оценок от точечных оценок параметров распределения по результатам выборки? Почему говорят, что интервал покрывает значение параметра с заданной надежностью, а концы интервала случайные величины? Что мы называем “надежностью”?

· В чем заключается метод моментов для точечной оценки параметров распределения?

· В чем состоит метод наибольшего правдоподобия?

· Могут ли коррелированные признаки элементов выборочной совокупности быть независимыми? Что значит равенство выборочного коэффициента корреляции ±1?

Вариант № 31

X– число членов семьи, занимающегося фермерским хозяйством (ед.)

Y – прибыль, получаемая фермерским хозяйством в среднем за сезон (тыс. долларов.)

Заданный признак: X и γ = 0.95

Таблицу частот см в вашем задании, файл «Вариант задания 4»

Вопросы

1. Классическая формула вычисления вероятности.

2. Геометрическая вероятность.

3. Статистическое определение вероятности и его применение.

4. Теоремы сложения и умножения.

5. Формулы полной вероятности и Байеса.

6. Повторение опытов. Формула Бернулли. Мода биноминального распределения.

7. Повторение опытов (при большом n). Формула Пуассона.

8. Повторение опытов (при большом n). Теорема Муавра-Лапласа.

9. Повторение опытов (при большом n). Интегральная теорема Муавра-Лапласа.

10. Дискретная случайная величина. Способы задания.

11. Биномиальное распределение и его характеристики.

12. Распределение Пуассона и его характеристики.

13. Геометрическое распределение и его характеристики.

14. Гипергеометрическое распределение.

15. Математическое ожидание и его свойства.

16. Вероятностный смысл математического ожидания.

17. Дисперсия, ее свойства, вероятностный смысл.

18. Непрерывная случайная величина. Способы её задания.

19. Функция распределения дискретной и непрерывной случайной величины и ее свойства.

20. Плотность распределения и ее свойства.

21. Нормальное распределение. Стандартное нормальное распределение и его свойства.

1. Числовые характеристики случайной величины, начальные, центральные и эмпирические моменты. Являются ли они случайными величинами?
2. Нормальное распределение, нормальная кривая, его мода и медиана, асимметрия и эксцесс.

24. Математическое ожидание и дисперсия непрерывной случайной величины.

25. Равномерное непрерывное распределение и его свойства.

26. Закон больших чисел.

27. Центральная предельная теорема.

28. Система двух дискретных случайных величин и ее характеристики.

29. Система двух непрерывных случайных величин и ее характеристики.

30. Теорема о необходимом и достаточном условии независимости компонент двух мерной случайной величины.

31. Плотности компонент двух мерной случайной величины и условные вероятности.

32. Условные математические ожидания, линия регрессии.

33. Корреляционный момент, коэффициент корреляции. Коррелированность и независимость компонент.

34. Функции одной случайной величины, дискретной и непрерывной. Закон распределения и числовые характеристики.

35. Статистическое распределение выборки, эмпирическая функция распределения, полигон и гистограмма.

36. Точечные оценки. Основные определения. Несмещённость, эффективность и состоятель­ность.

37. Метод наименьших квадратов для определения линии линейной регрессии, эмпирический коэффициент корреляции.

38. Метод произведений для вычисления эмпирического коэффициента корреляйции.

39. Метод моментов. Условные варианты и метод произведений для определения математического ожидания, дисперсии, асимметрии и эксцесса

40. Метод наибольшего правдоподобия.

41. Интервальные оценки параметров распределений.

42. Проверка статистических гипотез. Основные определения.

43. Проверка гипотез о числовых характеристиках генеральной совокупности.

44. Критерии согласия Пирсона.

Задачи

КЛАССИЧЕСКАЯ ФОРМУЛА ВЫЧИСЛЕНИЯ ВЕРОЯТНОСТИ

N1.

Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.

N2.

В партии из N деталей имеется n стандартных. Наудачу отобраны m деталей. Найти' вероятность того, что среди отобранных деталей ровно k стандартных.

N3.

В цехе работают 6 мужчин и 4 женщины. По табельным номерам наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных лиц окажутся 3 женщины.

N4.

На складе имеется 15 кинескопов, причем 10 из них изготовлены Львовским заводом. Найти вероятность того, что среди наудачу взятых пяти кинескопов окажутся 3 кинескопа Львовского завода.

N5.

В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов окажутся 5 отличников.

N6.

В коробке имеется 5 одинаковых изделий, причем 3 из них окрашены. Наудачу извлечены 2 изделия. Найти вероятность того, что среди извлеченных двух изделий окажутся: а) одно окрашенное изделие; б) два окрашенных изделия.

N7.

В коробке имеется 5 одинаковых изделий, причем 3 из них окрашены. Наудачу извлечены 2 изделия. Найти вероятность того, что среди извлеченных двух изделий окажется хотя бы одно окрашенное изделие.

N8.

"Секретный" замок содержит на общей оси 4 диска, каждый из которых разделен на 5 секторов с различными написанными на них цифрами. Замок открывается только в том случае, если диски установлены так, что цифры дисков образуют определенное четырехзначное число. Найти вероятность того, что при произвольной установке дисков замок можно будет открыть.

N9.

Отдел технического контроля обнаружил 5 бракованных книг из 50 просмотренных в партии из 100 книг. Найти вероятность обнаружить оставшиеся бракованные при просмотре еще 10 книг, если всего в партии 7 бракованных.

N10.

В партии из 10 приборов 1 негодный. Взяли 2 прибора. Найти вероятность того, что неисправный не попался.

ГЕОМЕТРИЧЕСКАЯ ВЕРОЯТНОСТЬ.

N11.

К автобусной остановке через каждые 4 минуты подходит автобус линии А и через каждые 6 минут - автобус линии В. Определить вероятность того, что первый подошедший автобус окажется автобусом линии А.

N12.

Два лица имеют одинаковую вероятность прийти к указанному месту в любой момент промежутка времени Т. Определить вероятность того, что время ожидания одним другого будет не больше t.

N13.

Какова вероятность того, что случайно выбранная на глобусе точка лежит за полярным кругом (66 градусов 33 минуты северной широты)?

N14.

Какова вероятность, не целясь, попасть бесконечно малой пулей в прутья квадратной решетки, если толщина прутьев равна а, а расстояние между их осями равно L (L>a).

N15.

На перекрестке установлен автоматический светофор, в котором 1 минуту горит зеленый свет и 0.5 минуты - красный, затем снова 1 минуту - зеленый и 0.5 минуты - красный,... . Какова вероятность для случайно подъехавшего автомобиля проехать перекресток без остановки?

N16.

Луч локатора перемещается в горизонтальной плоскости с постоянной угловой скоростью. Какова вероятность того, что цель будет обнаружена в угловом секторе А радиан, если появление цели по любому направлению равновозможно?)

N17.

Какова вероятность того, что сумма двух наудачу взятых отрезков , длина каждого из которых не превосходит L, будет больше L?

N18.

На шарик нанесена сетка географических координат. Шарик брошен на плоскость. Какова вероятность того, что шарик прикоснется к плоскости точкой, которая находится в области между 0 и 90-м градусами восточной долготы?

N 19.

Какова вероятность того, что шарик прикоснется к плоскости точкой, которая находится в области между45 и 90-м градусами северной широты? (см. условие предыдущей задачи).

N20.

В случайный момент времени х є [0,Т] появляется радиосигнал длительностью Т1. В случайный момент времени Y є [0, Т] включается приемник на время Т2<Т1. Найти вероятность обнаружения сигнала, если время настройки приемника равно Т3 (Т3<Т2<Т1).