Классическая формула вероятности

Если множество элементарных событий Ω={ω1,ω2,…ωN},конечно и все элементарные события равновозможны, то такая вероятностная схема носит название классической. В этом случае вероятность Р{А} наступления события А, состоящего из М элементарных событий, входящих в Ω, определяется как отношение числа М элементарных событий, благоприятствующих наступлению события А, к общему числу N элементарных событий. Эта формула носит название классической формулы вероятности: Р{А}= M/N.

В частности, согласно классической формуле вероятности:

Р{ωi }=1/N (i=1,2,... , N)

Р{Ω}= N/N =1

P{Æ}=0/N =0

Комбинаторика, 1) то же, что математический комбинаторный анализ. 2) Раздел элементарной математики, связанный с изучением количества комбинаций, подчинённых тем или иным условиям, которые можно составить из заданного конечного множества объектов (безразлично, какой природы; это могут быть буквы, цифры, какие-либо предметы и т.п.). Число размещений. Пусть имеется n различных предметов. Сколькими способами можно выбрать из них т предметов (учитывая порядок, в котором выбираются предметы)? Число способов равно A_n^m =? A_n^m называют числом размещений из n элементов по m. Число сочетаний. Пусть имеется n различных предметов. Сколькими способами можно выбрать из них т предметов (безразлично, в каком порядке выбираются предметы)? Число способов такого выбора равно C_n^m = 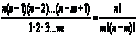C_n^m называют числом сочетаний из n элементов по m. Числа C_n^m получаются как коэффициенты разложения n-й степени двучлена: (a+b) ⁿ=C_n⁰aⁿ+ C_n¹a^n-1b +C_n²a^n-2b^{2 ?}+... + C_n^n-1ab^n-1 + C_nⁿ bⁿ, и поэтому они называются также биномиальными коэффициентами. Основные соотношения для биномиальных коэффициентов: C_n^m=C_n^n-m,C_n^m? + C_n^m+1 = C_n+1^m+1, C_n⁰ + C_n¹ + C_n²+...+ C_n^n-1+ C_nⁿ =2ⁿ, ? C_n⁰ - C_n¹ + C_n²-...+ (-1) ⁿC_nⁿ = 0. Числа A_n^m, P_m и C_n^m связаны соотношением: A_n^m=P_m C_n^m. Рассматриваются также размещения с повторением (т. е. всевозможные наборы из m предметов n различных видов, порядок в наборе существен) и сочетания с повторением (то же, но порядок в наборе не существен). Число размещений с повторением даётся формулой n^m, число сочетаний с повторением - формулой C^m_n+m-1.

Вопрос 4

При аксиоматическом построении вероятностей в каждом конкретном пространстве элементарных событий W выделяется s-поле событий S для каждого события AÎS задается вероятность P{A} – числовая функция, определенная на s-поле событий S и удовлетворяющая следующим аксиомам.

Аксиома неотрицательности вероятности для всех AÎS: P{A}³ 0.

Аксиома нормированности вероятности: P{W}=1.

Аксиома адаптивности вероятности: для всех A,BÎS,таких, что AÇB¹Æ: P{AÈB}=P{A} +P{B}

Вопрос 6

1) Условная вероятность события А при условии В равна Р(А/B)=P(A*B)/P(B), Р(В)>0.

2) Событие А не зависит от события В, если Р(А/B)=P(A). Независимость событий взаимна, т.е. если событие А не зависит от В, то событие В не зависит от А. В самом деле при Р(А)>0 имеем Р(B/A)=P(A*B)/P(A)=P(A/B)*P(B)/P(A)=P(A)*P(B)/P(A)=P(B). Вытекает следующая формула умножения вероятностей: Р(А*В)=Р(А)*Р(В/A). Для независимых событий вероятность произведения событий равна произведению их вероятностей: Р(А*В)=Р(А)*Р(В). 3) События А1,А2,…,Аn образуют полную группу событий, если они попарно несовместны и вместе образуют достоверное событие, т.е. Аi*Aj=0, i не=j, U по i от 1 до n Аi=омега.

Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило: Р(АВ)=Р(А)*Ра(В). В частности для независимых событий Р(АВ)=Р(А)*Р(В), т.е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.

Вопрос 7

Формула полной вероятности. Систему событий А₁, А₂, ...,A_N называют конечным разбиением (или просто разбиением), если они попарно несовместны, а их сумма образует полное пространство событий: А₁ + А₂ + ... + А_N = W.

Если события А_i образуют разбиение пространства событий и все P(A_i) > 0, то для любого события В имеет место формула полной вероятности: P(B) = 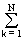P(A_k)×P(B/A_k),

что непосредственно следует из (8.2.14) для попарно несовместных событий:

B = B×W = BA₁+BA₂+...BA_N.

P(B) = P(BA₁)+P(BA₂)+... +P(BA_N) = P(A₁)P(B/A₁)+P(A₂)P(B/A₂)+...+P(A_N)P(B/A_N).

Вопрос 8

Формула баеса

Вопрос 9

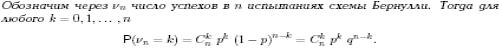
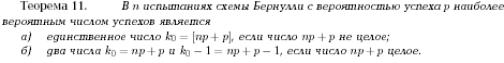
Вопрос 10

Случайной величиной называется числовая величина, которая в результате опыта может принять какое-либо значение из некоторого множества, причем заранее, до проведения опыта, невозможно сказать, какое именно значение она примет. Случайные величины обозначают заглавными латинскими буквами X, Y, Z,..., а их возможные значения — строчными латинскими буквами х, у, z. Случайная величина называется дискретной, если множество ее значенийконечно или счетно, и непрерывной в противном случае. Законом распределения случайной величины называется любое со­отношение, связывающее возможные значения этой случайной ве­личины и соответствующие им вероятности. Закон распределения дискретной случайной величины задается чаще всего не функцией распределения, а рядом распределения, т.е, таблицей

Х	x1	x2	...	xn	...
P	p1	p1	...	pn	...

В которой x1, x2, ..., xn, ... - расположенные по возрастанию значения дискретной случайной величины X, а р1, р₂, ..., р_п, ... — отвечающие этим значениям вероятности: p_i = Р{Х = хi), i=1, 2, ..., п, ... . Число столбцов в этой таблице может быть конечным (если соответствующая случайная величина принимает конечное число значений) или бесконечныи. Очевидно,Spi=1.

Многоугольником распределения дискретной случайной величины X называется ломаная, соединяющая точки {xi; pi), расположенные в Порядке возрастания хi.

Вопрос 11

Функцией распределения случайной величины Х называется функция F_X(x)= P{X<x}, xÎR

Под {X<x}понимается событие, состоящее в том, что случайная величина Х принимает значение меньшее, чем число х. Если известно, о какой случайной величине идёт речь, то индекс, обозначающий эту случайную величину, опускается: F(x) ºF_X(x).

Как числовая функция от числового аргумента х, функция распределения F(x) произвольной случайной величины Х обладает следующими свойствами:

1)для любого xÎR: 0£F(x) £ 1

2) F(-¥) = lim_x®¥F(x) = 0 ; F(+¥) = lim_x®¥F(x) = 1;

3) F(x)-неубывающая функция, т.е.для любых х1,х2 ÎR таких, что х1<х2: F(x1) £F(x2);

4)для любого xÎR: F(x)= F(x-0)= lim_z<x,z®xF(z).

Вопрос 12

Мат. Ожиданием Д.С.В. называют сумму произведений всех ее возможных значений на их вероятности: М(Х)=х1р1+х2р2+…+хnpn. Если Д.С.В. принимает счетное множество возможных значений, то М(Х)=сумма по i от 1 до бесконечности xipi, причем мат. ожидание существует, если ряд в правой части равенства сходится абсолютно. Мат. ожидание обладает следующими свойствами: 1) Мат. ожидание постоянной величины равно самой постоянной: М(С)=С. 2) Постоянный множитель можно выносить за знак мат. ожидания: М (СХ)=СМ (Х). 3) Мат. ожидание произведения взаимно независимых С.В. равно произведению мат. ожиданий сомножителей: М (Х1,Х2…Хn)=M(X1)*M(X2)…M(Xn). 4) Мат. ожидание суммы С.В. равно сумме мат. ожиданий слагаемых: М (Х1+Х2+Х3+…+Хn)=M(X1)+M(X2)+M(X3)+…+M(Xn).

Вопрос13

Дисперсией случайной величины х называется число: DX= M(X-MX)² ,равное математическому ожиданию квадрата отклонения случайной величины от своего математического ожидания. Для вычисления дисперсии иногда проще использовать формулу: DX=M(X²)-(MX)² . Для дискретных св:

DX=∑(xi – MX)² pi;

DX=∑xi²pi – (MX) ².

Свойства дисперсии дискретной случайной величины: (X,Y-независимые д.св, с- неслучайная постоянная ÎR)

Dc=0;

D(cX)=c²DX;

D(X+Y)= DX + DY

Вопрос 15

Случайная величина Х наз.распределённой по геометрическому закону с параметром р (рÎ[0;1]), если она принимает значения 1,2,3… с вероятностямиР{Х=х}= р(1-р)^х-1 (х = 1,2,3…).

Случайную величину Х можно интерпритировать как число испытаний Бернулли, которые придётся произвести до первого успеха, если успех в единичном испытании может произойти с вероятностью р.

Математическое ожидание случайной величины, имеющей геометрическое распределение: МХ=1/p.

Дисперсия: DX=1-p/p²

Вопрос 16

Если число испытаний велико, а вероятность P повяления события в каждом испытнаии очень мала, то используют приближенную формулу

Pn(k)=l^k*e^(-l/k)

Где k – число появлений события в n независимых испытаниях, l = np (среднее число появлений события в n независимых испытаниях), и говорят, что случайная величина распределена по закону Пуассона.

Вопрос 17

С.В. Х называется непрерывной, если существует неотрицательная функция рх(х) такая, что при любых х функцию распределения Fx(x) можно представить в виде: Fx(x)=интеграл от –бесконечности до х px(y)dy. Рассматривают только такие С.В., для которых рх(х) непрерывна всюду, кроме, может быть, конечного числа точек. Плотностью распределения вероятностей непрерывной С.В. называют первую производную от функции распределения: f(x)=F’(x). Вероятность того, что Н.С.В. Х примет значение, принадлежащее интервалу (а,b), определяется равенством P(a<X<b)=интервал от а до bf(x)dx. Зная плотность распределения можно найти функцию распределения F(x)=интеграл от –бесконечности до х f(x)dx. Плотность распределения обладает следующими свойствами: 1) П.Р. неотрицательна, т.е. f(x)>=0. 2) Несобственный интеграл от плотности распределения в пределах от –бесконечности до бесконечности равен единице: интеграл от –бесконечности до бесконечности f(x)dx=1.

Вопрос 18

Мат. ожидание Н.С.В. Х, возможные значения которой принадлежат всей оси ОХ, определяется равенством: М(Х)=интеграл от –бесконечности до бесконечности хf(x)dx, где f(x) - плотность распределения С.В. Х. Предполагается, что интеграл сходится абсолютно. В частности, если все возможные значения принадлежат интервалу (а,b), то М(Х)=интеграл от а до bxf(x)dx. Все свойства мат. ожидания, указаны выше, для Д.С.В. Они сохраняются и для Н.С.В.

Дисперсия Н.С.В. Х, возможные значения которой принадлежат всей оси ОХ, определяется равенством: D(X)=интеграл от –бесконечности до бесконечности [x-M(X)]*2f(x)dx, или равносильным равенством: D(X)=интеграл от –бесконечности до бесконечности x*2f(x)dx – [M(X)]*2. В частности, если все возможные значения х принадлежат интервалу (a,b),то D(X)=интервал от а до b [x – M(X)]*2f(x)dx,или D(X)=интеграл от

Вопрос 19

Моменты распределения.При решении многих практических задач нет особой необходимости в полной вероятностной характеристике каких-либо случайных величин, которую дает функция плотности распределения вероятностей. Очень часто приходится также иметь дело с анализом случайных величин, плотности вероятностей которых не отображаются аналитическими функциями либо вообще неизвестны. В этих случаях достаточно общее представление о характере и основных особенностях распределения случайных величин можно получить на основании усредненных числовых характеристик распределений.

Числовыми характеристиками случайных величин, которые однозначно определяются функциями распределения их вероятностей, являются моменты.

Начальные моменты n-го порядка случайной величины X (или просто моменты) представляют собой усредненные значения n-й степени случайной переменной: m_nº М{Xⁿ}º 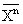= 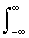xⁿ p(x) dx, где M{Xⁿ} и 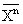- символические обозначения математического ожидания и усреднения величины Хⁿ, которые вычисляются по пространству состояний случайной величины Х.