Применения обобщенной флаттерной характеристики; опыты в скоростных аэродинамических трубах
Создавать для испытания в аэродинамических трубах малых скоростей модели с масштабом масс, удовлетворяющим равенству Кm = KL3, удается только потому, что при малых скоростях потока для достижения флаттера требуется иметь малую жесткость модели (обычно в 50-100 раз меньше натурной в сопоставимых величинах).
Иным оказывается положение при моделировании флаттера в скоростных аэродинамических трубах, где достижение натурных значений числа Мтр = МH происходит при скоростных напорах qтр того же порядка, что и в полете. По этой причине модель для скоростной аэродинамической трубы должна быть по сравнению с моделью для аэродинамической трубы малых скоростей в 50-100 раз относительно более жесткой. Вследствие этого при применении освоенных конструктивных схем и типов моделей в большинстве случаев удавалось создавать лишь модели с Кm > KL3, точнее, Кm = KпKL3, где Кп = 2-8- коэффициент перетяжеления. В редких случаях коэффициент Кп достигал меньшего значения.
Методика испытаний моделей при исследовании флаттера в скоростных аэродинамических трубах состоит в том, что, изменяя по какому-либо закону Dтр и Мтр, определяют значение qкр тр, при котором в аэродинамической трубе возникает флаттер исследуемой модели. Варьируя закон изменения Dтр и Мтр, получают некоторую совокупность значений qкр тр при различных Dтр и М.
Пересчитав результаты испытаний модели, можно в координатах (М, D, q) построить пространственную кривую, изображающую зависимость qH кр от Dн и М (рис. 29).
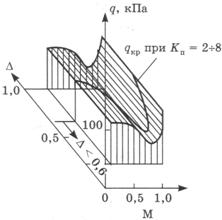
Рисунок 29. Форма флаттерной поверхности при автомодельности по D
При Кп = 2-8 эта кривая будет располагаться в области малых значений DH, соответствующим условиям полета на больших высотах, где достижимые скоростные напоры малы. Вследствие этого полет на таких высотах не должен оказаться опасным по условиям возникновения флаттера.
Однако полученные результаты не позволяют ответить на вопрос о безопасности от флаттера исследуемого летательного аппарата во всей области интересующих значений DH. И до тех пор, пока будут применяться конструктивные схемы моделей, не позволяющие в должной степени уменьшить Кп, придется при анализе результатов испытаний моделей в скоростной аэродинамической трубе пользоваться в первом приближении тем же самым предположением о существовании для ряда случаев области автомодельности по величине ρL3/m. В рамках предположения о существовании при флаттере области автомодельности по величине ρL3/m вплоть до ρL3/m для сжимаемого потока можно через кривую на рисунке 29 провести цилиндрическую поверхность с образующими, параллельными оси D, и считать, что она изображает зависимость qH кр во всей области изменения Dн. Пересечение этой поверхности с поверхностью qH(DH, М) определит границу области флаттера для реальных условий полета. Обычно на практике при сделанных предположениях удобно пользоваться проекцией пространственной кривой qH кр(DH, М) на координатную плоскость (М, q), предварительно нанеся на эту плоскость семейство кривых, изображающих зависимость величины qH для различной высоты полета Н (рис. 30).
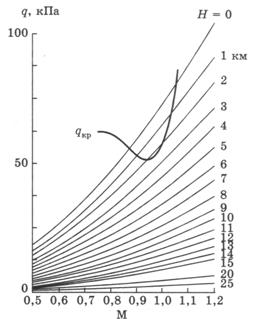
Рисунок 30. Проекция флаттерной поверхности на плоскость (М, q)
По точкам пересечения qH кр с семейством qH можно в рамках принятых допущений приближенно определить границу области флаттера исследуемого летательного аппарата в координатах (М, Н).
Очевидно, что точность опытов с перетяжеленными моделями зависит от того, насколько близкими окажутся значения Dтр/Кп и DH при которых qHкр = qH. Следовательно, перетяжеленные модели больше подходят для исследования флаттерных характеристик высотных самолетов. Подчеркнем, что степень достоверности предположения об автомодельности по параметру ρL3/m, будет тем выше, чем относительно более тяжелым является исследуемый летательный аппарат и чем при больших высотах Н находится интересующая область полетов. Но существенное уменьшение массы летательного аппарата m, должно привести к увеличению q.
Литература
1. В.В. Лыщинский, Моделирование флаттера в аэродинамических трубах, Москва, Физматлит, 2009
