Тема 6 МОДЕЛИРОВАНИЕ ФЛАТТЕРА В АЭРОДИНАМИЧЕСКОЙ ТРУБЕ

Тема 6 МОДЕЛИРОВАНИЕ ФЛАТТЕРА В АЭРОДИНАМИЧЕСКОЙ ТРУБЕ

Исследования явления флаттера проводят в аэродинамических трубах (АДТ) с помощью моделей уменьшенного масштаба. При выполнении определенных критериев подобия между натурной конструкцией самолета и его уменьшенной моделью удается с требуемой точностью при меньших затратах времени и средств, без всякой угрозы для безопасности экипажа (которая существует при испытаниях натурной конструкции) исследовать такие опасные явления аэроупругости, как флаттер, дивергенция, реверс элеронов и др. Кроме того, простые модели позволяют выявить суть явления, отделить важные факторы от второстепенных, провести параметрические исследования, определить пути совершенствования конструкции, установить границы безопасных режимов полета. Моделирование флаттера в АДТ основывается на подходах, которые применяют для построения кинематически подобных систем.

Кинематически подобные системы сохраняют геометрическое подобие друг другу не только в статическом положении, но и в течение всего времени их движения. Для реализации подобия этих движений необходимо знать, каким именно требованиям должны удовлетворять такие системы. Данная задача была решена Ньютоном.

Решение оказалось прямым следствием второго закона Ньютона.

По второму закону Ньютона для систем 1 и 2 имеем:

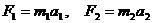
Подобие движений будет обеспечено, если ускорения систем всегда будут оставаться пропорциональными. Тогда:

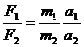
и, следовательно, в масштабных коэффициентах 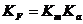, где

K_F - масштаб сил,

K_m - масштаб масс,

K_a - масштаб ускорений.

Выразив масштабы ускорений через масштабы времени и линейных размеров, формулу можно записать в окончательном ви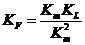де:

, где

K_t - масштаб времени,

K_L масштаб линейных размеров, обеспечивающий геометрическое подобие при движении обеих систем в соответствующие моменты времени.

Системы, параметры которых удовлетворяют формуле Ньютона, будут совершать кинематически подобные движения.

Следует особо подчеркнуть, что уравнение связывает четыре величины. Поэтому любые три из них могут быть заданы произвольно, а оставшаяся четвертая величина однозначно должна быть определена по формуле Ньютона. Последнее обстоятельство и является тем требованием, выполнение которого обеспечивает кинематическое подобие движения рассматриваемых систем.

Вопросы подобия

Для исследования в аэродинамических трубах малых скоростей флаттера самолетов с крыльями большого удлинения применяют отсечно-балочную модель. В моделях этой схемы (рис. 1) жесткостные характеристики крыла, фюзеляжа, оперения моделируются балками-лонжеронами переменного сечения (рис. 2), расположенными по осям жесткости.

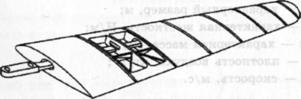
Рисунок 1. Отсечно-балочная модель крыла

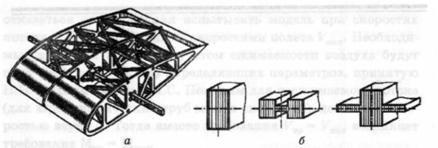
Рисунок 2. Основные элементы моделей: а) отсек; б) лонжероны с различной формой сечений

Аэродинамические обводы воспроизводят жесткими, отделенными друг от друга щелями, отсеками, закрепленными на балках-лонжеронах так, чтобы не стеснять их деформаций при колебаниях модели. На лонжероны и отсеки закрепляют доводочные грузы, обеспечивающие подобие модели по массово-инерционным характеристикам. Отсеки передают на лонжероны аэродинамические нагрузки.

Модели этой схемы успешно применяют в трубах малых скоростей для исследования флаттера самолетов, имеющих несущие и управляющие поверхности большого и умеренного удлинения.

Следует отметить, что модели отсечно-балочной схемы малопригодны для моделирования флаттера ЛА с несущими и управляющими поверхностями малого удлинения, когда на модели невозможно воспроизвести упругие характеристики натуры балкой. Такие модели также не следует использовать при числах М>0,6-0,7, потому что на стыках между отсеками модели могут возникать местные скачки уплотнения, тогда как в натурных условиях скачки такого типа возникать не будут.

О подобии по числу Струхаля

Дополним систему размерных параметров (1), определяющих явление флаттера, еще одной размерной величиной — частотой колебаний ω. Для удобства преобразуем размерность жесткости f, введя размерности массы (кг) и ускорения (м/с²):

L – характерный размер, м;

f – характерная жесткость, кг/с²;

m – характерная масса, кг; (4)

ρ – плотность воздуха, кг/м³;

V – скорость, м/с.

ω – частота колебаний, 1/с.

Из шести размерных параметров в технической системе единиц составим согласно «π» теоремы анализа размерностей три независимые безразмерные комбинации:

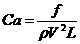- число Коши (5)

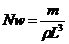- число Ньютона (6)

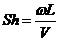- число Струхаля (7)

Используем тот факт, что величина 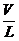так же как и величина 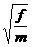имеет размерность ω 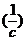, и поэтому комбинация:

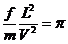
(8)

будет безразмерной величиной.

Запишем (7), (8) в масштабных коэффициентах:

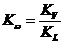(9)

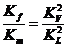(10)

откуда:

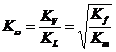(11)

Равенство (11) получено из анализа размерностей. При их выводе не требовалось учитывать индивидуальные особенности изучаемых колебаний. Поэтому масштаб частот K_ω должен быть одинаков для самых различных видов колебаний (в пустоте, в потоке воздуха, при флаттере и т.п.). Подчеркнем, что кроме условий Ca=item и Nw=item должны быть выполнены и другие необходимые для моделирования изучаемого явления критерии подобия.

Заметим, что частоты внешних воздействий на ЛА при моделировании, например, полета в неспокойном воздухе следует, конечно, задавать в соответствии с K_ω. Обратим внимание, что:

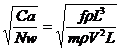=Sh (12)

Равенство (12) означает, что каждая из величин Ca, Nw, Sh может быть выражена через две другие:

,

,

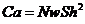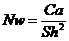т.е. величины Ca, Nw, Sh не являются независимыми.

По поводу полученного результата сделаем два замечания.

1. В «π» теореме устанавливается, что независимых безразмерных комбинаций из n размерных величин, описывающих явление, можно составить:

n-m, где

m - число основных единиц выбранной системы измерений.

Способ составления безразмерных комбинаций теоремой не регламентируется и поэтому их выбор может оказаться не единственным.

2. Числа Ca, Nw, хотя и не содержат ω - размерной величины, характеризующей колебания исследуемого объекта, но параметры модели, режимы ее испытаний и частоты колебаний однозначно определяются требованиями подобия Ca=item и Nw=item. И поэтому при модельных испытаниях подобие всех процессов в рамках, сделанных предположений, должно соблюдаться автоматически.

Флаттер органов управления

Из всех летных происшествий, когда на ЛА возникал флаттер, большая часть приходилась на флаттер органов управления. Особенно участились такие случаи при достижении ЛА трансзвуковых скоростей полета. В этот же период времени был обнаружен факт возникновения отрицательного демпфирования при колебаниях рулевых поверхностей, когда числа М достигали значений, близких к единице. Объяснялся этот факт неустойчивостью местных скачков уплотнения, перемещающихся вдоль хорды рулевых поверхностей при их вращательных колебаниях. В этих случаях для возникновения автоколебаний не требовалось участия в явлении иных степеней свободы, кроме вращения органа управления вокруг оси навески. Такие колебания получили название «флаттер с одной степенью свободы», «маховая тряска». Этим подчеркивалось их принципиальное отличие от случаев обычного «классического» флаттера, когда в явлении участвуют как минимум две степени свободы.

Поскольку главной причиной явления этого типа считалось движение местных скачков уплотнения, то автоколебания должны были начинаться при достижении строго определенного числа М_кр, почти независимо от величины скоростного напора q. Кроме того, автоколебания не могли быть «излечены» путем весовой балансировки органов управления. Иными словами, в таких случаях автоколебания лишались черт, присущих «классическим» формам флаттера.

Для исследования этого явления был поставлен опыт в скоростной аэродинамической трубе на специальной установке, которая должна была обеспечить вращательные колебания с одной степенью свободы отсека крыла относительно оси, параллельной передней кромке. Внешне картина автоколебаний выглядела именно так‑присутствовала одна степень свободы‑поворот отсека крыла вокруг оси вращения.

Но на самом деле это впечатление оказалось ошибочным, поскольку автоколебания удалось устранить путем установки на отсек крыла выносных балансиров. Это свидетельствовало об участии в колебаниях других степеней свободы, хотя при конструировании установки были приняты специальные меры, чтобы исключить колебания более чем с одной степенью свободы.

Примерно в это же время в зарубежной литературе появилось описание установки для исследования флаттера с одной степенью свободы, в которой для обеспечения колебаний только с одной степенью свободы были приняты экзотические меры. В качестве крыла использовалась высокопрочная стальная лента длиной 500 мм с обтекаемым сечением, имевшая хорду 50 мм. Лента была заделана по концам в подшипники, обеспечивавшие вращение вокруг продольной оси. Дополнительно она растягивалась усилием - 50000 Н, чтобы исключить возможность изгиба.

Очевидно, что установки такого типа могут предназначаться только для физических опытов с целью проверки принципиальных выводов теории. При этом очень важно, чтобы явление не искажалось сопутствующими факторами. Напротив, задача моделирования флаттера реальных ЛА требует воспроизводить натуру с максимально возможным числом степеней свободы. Поэтому от физических опытов по исследованию колебаний с одной степенью свободы нельзя требовать исчерпывающих сведений о безопасности от флаттера реальной конструкции, которая всегда является многостепенной.

В подтверждение этого сошлемся на летное происшествие при испытаниях одного из опытных самолетов. При достижении этим самолетом числа М = 0,93 возникли колебания киля с рулем направления, приведшие к разрушению законцовки киля и верхней части руля направления.

Для исследования этого случая была разработана и испытана модель киля с рулем. На модели приближенно моделировались жесткости на изгиб и кручение киля и руля направления. Кроме того, была предусмотрена возможность варьирования жесткости проводки управления рулем.

В исходном варианте на этой модели при М ~ 0,93 возникли мощные колебания киля и руля с частотой, совпавшей после пересчета на натуру по масштабным коэффициентам, с частотой колебаний, зафиксированной в полете. Величина достигнутого при этом скоростного напора возрастала при увеличении степени весовой балансировки руля направления. Была предпринята попытка выяснить, какова роль других (кроме вращения руля) степеней свободы в возникших колебаниях. С этой целью модель была расчалена несколькими тонкими расчалками, перпендикулярными плоскости киля, оставлявшими лишь свободу вращения руля и исключавшими возможность деформаций киля и руля (рис. 9). При этих условиях в обследованном диапазоне М и q колебания модели не возникали.

В заключение отметим, что, поскольку эти исследования проводились не на целых моделях ЛА, а на моделях его частей — килей (рис. 10), стабилизаторов и крыльев, то их масштаб длин K_L мог быть существенно увеличен.

За счет этого пропорционально увеличивалось число Рейнольдса (Re). За счет увеличения плотности воздуха в рабочей части трубы при одновременном увеличении масштаба жесткостей модели появилась возможность достигать натурных значений числа Re. В результате стало реальным одновременно соблюсти требования подобия как по сжимаемости, так и по вязкости воздуха (М_м = М_н, Re_M = Re_H). При этом было выяснено следующее. Поскольку скорость звука а и вязкость воздуха μ связаны с температурой воздуха Т в рабочей части (а ~ Т^1/2, m~ Т^3/4), то соотношения М_м = М_н, Re_M = Re_H накладывают дополнительные условия на свободу выбора масштаба плотности К_ρ и скоростного напора K_q - оба этих масштаба оказываются зависимыми от масштаба длины K_L.

Использование крупномасштабных моделей для исследований флаттера органов управления в промышленной аэродинамической трубе позволило решить и весьма важную практическую задачу — создать модели (рис. 11) с демпферами. Гидравлические демпферы применяют для устранения в потоке колебаний отклоняющихся поверхностей и часто оказываются единственным реальным средством борьбы с флаттером органов управления скоростных ЛА. При этом очевидное на первый взгляд решение — применить принцип конструктивного подобия и оснастить модели уменьшенными копиями гидравлических демпферов — на практике связано с техническими трудностями обеспечения необходимой герметичности всех полостей демпфера.

Сечениие А-А

Вопросы методики испытаний динамически подобных моделей при сверхзвуковых скоростях. Регулируемое сопло

Принципиальные трудности испытания динамически подобных моделей при сверхзвуковых скоростях обусловлены невозможностью плавной регулировки скорости потока (числа М) в процессе запуска скоростных аэродинамических труб. Как правило, аэродинамические трубы оснащены лишь набором жестких сопел, геометрия которых рассчитана для получения ряда дискретных значений чисел М, при которых реализовалось установившееся течение. Но при запуске аэродинамической трубы (до достижения расчетного для данного сопла числа М) течение неустановившееся. В нем возникают нерасчетные скачки уплотнения, из-за чего во время запуска аэродинамической трубы на модель действуют огромные силы, представлявшие серьезную опасность. Такая же ситуация имеет место и при остановке аэродинамической трубы.

При аэродинамических исследованиях избежать опасности разрушения удается путем применения высокопрочной стали, обеспечив, таким образом, достаточную прочность моделей. Для динамически подобных моделей такая возможность отсутствует из-за необходимости соблюдения подобия по жесткостным характеристикам, что неизбежно приводит к уменьшению прочности моделей.

Поэтому вводят модель в установившийся поток после выхода трубы на расчетный режим, а выводят модель из потока до начала остановки. Механизмы, обеспечивающие ввод моделей, созданы в нескольких вариантах: для испытания моделей консолей (рис. 16) и моделей объекта в «свободном» полете на буксире.

Рисунок 16. Модель крыла на механизме ввода

Рисунок 17. Механизмы ввода для аэродинамической трубы: 1 — плиты механизма ввода, 2 — створки, 3 — пневмозамки, 4 — каретка механизма

Механизмы ввода в поток представляет собой многофункциональную установку (рис. 17). Консоли моделей могут поочередно вводиться в рабочую часть в течение одного пуска. Модели целого самолета закрывают во время пуска прочными чехлами, которые затем дистанционно выводят из потока и освобождают модель.

Применение механизмов ввода для исследования флаттера при сверхзвуковых скоростях используют в том случае, когда АДТ не оснащена регулируемым соплом (PC), позволяющим плавно достигать необходимого числа М во всем рабочем диапазоне скоростей потока. Пол и потолок регулируемого сопла выполняют в виде гибких плит, которые с помощью десятков дистанционно управляемых мощных гидравлических домкратов изгибают по расчетной поверхности, создавая нужный контур сопла (рис. 18).

Рисунок 18. Схема регулируемого сопла: 1 — жесткий участок, 2, 3 — гидродомкраты, 4 - гибкий участок, 5,6,7 — гидродомкраты, 8 — жесткая опора, 9 — потолок рабочей части, 10 — серьга

Механизмы ввода используют и при наличии регулируемого сопла для ускорения эксперимента и экономии сжатого воздуха. Закрепленные на механизмах ввода модели испытывают поочередно, без остановки потока.

Литература

1. В.В. Лыщинский, Моделирование флаттера в аэродинамических трубах, Москва, Физматлит, 2009

Тема 6 МОДЕЛИРОВАНИЕ ФЛАТТЕРА В АЭРОДИНАМИЧЕСКОЙ ТРУБЕ

Исследования явления флаттера проводят в аэродинамических трубах (АДТ) с помощью моделей уменьшенного масштаба. При выполнении определенных критериев подобия между натурной конструкцией самолета и его уменьшенной моделью удается с требуемой точностью при меньших затратах времени и средств, без всякой угрозы для безопасности экипажа (которая существует при испытаниях натурной конструкции) исследовать такие опасные явления аэроупругости, как флаттер, дивергенция, реверс элеронов и др. Кроме того, простые модели позволяют выявить суть явления, отделить важные факторы от второстепенных, провести параметрические исследования, определить пути совершенствования конструкции, установить границы безопасных режимов полета. Моделирование флаттера в АДТ основывается на подходах, которые применяют для построения кинематически подобных систем.

Кинематически подобные системы сохраняют геометрическое подобие друг другу не только в статическом положении, но и в течение всего времени их движения. Для реализации подобия этих движений необходимо знать, каким именно требованиям должны удовлетворять такие системы. Данная задача была решена Ньютоном.

Решение оказалось прямым следствием второго закона Ньютона.

По второму закону Ньютона для систем 1 и 2 имеем:

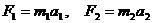
Подобие движений будет обеспечено, если ускорения систем всегда будут оставаться пропорциональными. Тогда:

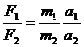
и, следовательно, в масштабных коэффициентах 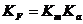, где

K_F - масштаб сил,

K_m - масштаб масс,

K_a - масштаб ускорений.

Выразив масштабы ускорений через масштабы времени и линейных размеров, формулу можно записать в окончательном ви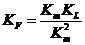де:

, где

K_t - масштаб времени,

K_L масштаб линейных размеров, обеспечивающий геометрическое подобие при движении обеих систем в соответствующие моменты времени.

Системы, параметры которых удовлетворяют формуле Ньютона, будут совершать кинематически подобные движения.

Следует особо подчеркнуть, что уравнение связывает четыре величины. Поэтому любые три из них могут быть заданы произвольно, а оставшаяся четвертая величина однозначно должна быть определена по формуле Ньютона. Последнее обстоятельство и является тем требованием, выполнение которого обеспечивает кинематическое подобие движения рассматриваемых систем.

Вопросы подобия

Для исследования в аэродинамических трубах малых скоростей флаттера самолетов с крыльями большого удлинения применяют отсечно-балочную модель. В моделях этой схемы (рис. 1) жесткостные характеристики крыла, фюзеляжа, оперения моделируются балками-лонжеронами переменного сечения (рис. 2), расположенными по осям жесткости.

Рисунок 1. Отсечно-балочная модель крыла

Рисунок 2. Основные элементы моделей: а) отсек; б) лонжероны с различной формой сечений

Аэродинамические обводы воспроизводят жесткими, отделенными друг от друга щелями, отсеками, закрепленными на балках-лонжеронах так, чтобы не стеснять их деформаций при колебаниях модели. На лонжероны и отсеки закрепляют доводочные грузы, обеспечивающие подобие модели по массово-инерционным характеристикам. Отсеки передают на лонжероны аэродинамические нагрузки.

Модели этой схемы успешно применяют в трубах малых скоростей для исследования флаттера самолетов, имеющих несущие и управляющие поверхности большого и умеренного удлинения.

Следует отметить, что модели отсечно-балочной схемы малопригодны для моделирования флаттера ЛА с несущими и управляющими поверхностями малого удлинения, когда на модели невозможно воспроизвести упругие характеристики натуры балкой. Такие модели также не следует использовать при числах М>0,6-0,7, потому что на стыках между отсеками модели могут возникать местные скачки уплотнения, тогда как в натурных условиях скачки такого типа возникать не будут.