Особенности моделирования информационных потоков

В системе массового обслуживания (СМО) описываются многие реальные системы: вычислительные системы, узлы сетей связи, системы посадки самолетов, поликлиники, супермаркеты, производственные участки − любые системы, где возможны очереди и (или) отказы в обслуживании. В распределенной автоматизированной системе сопровождения и контроля работ роль обслуживающего прибора играет компьютерное оборудование, роль заявок − выполняемые системой задачи. Источником заявок служат запросы на обработку и получение информации от прибора обслуживания. Моментом выдачи заявки является момент поступления запроса.

Целью использования СМО как модели является анализ качества функционирования указанных систем. В свою очередь, сети массового обслуживания (СеМО) используют для определения важнейших системных характеристик прогнозирования трафика:

· производительности оборудования;

· времени выполнения заявок;

· области допустимых значений нагрузки, при которых обеспечивается требуемое качество обслуживания и др.

Сеть массового обслуживания представляет собой совокупность конечного числа N обслуживающих узлов, в которой циркулируют заявки, переходящие в соответствии с маршрутной матрицей из одного узла в сервер через канал связи. Узел всегда является разомкнутой СМО (причем СМО может быть любого класса). При этом отдельные СМО отображают функционально самостоятельные части реальной системы, связи между СМО − структуру системы, а требования (заявки), циркулирующие по СеМО, − составляющие материальных или информационных потоков (сообщения (пакеты) в коммуникационной сети, задания в мультипроцессорных системах, сборочные единицы в производстве, контейнеры грузопотоков и т.п.).

В теории СеМО фундаментальным является понятие состояния сети. Важнейшая характеристика сетей массового обслуживания − вероятности их состояний. Для определения вероятностей состояний СеМО исследуют протекающий в сети случайный процесс. В качестве моделей протекающих в СеМО процессов наиболее часто используют марковские и полумарковские.

Марковским процессом с непрерывным временем описывают функционирование экспоненциальных СеМО (входящие потоки требований в каждую СМО пуассоновские, а времена каждого этапа обслуживания, реализуемого на любой СМО сети, имеют экспоненциальное распределение). Это позволяет считать, что этапы обслуживания независимы между собой и не зависят ни от параметров входящего потока, ни от состояния сети, ни от маршрутов следования заявок. Общая классификация сетей массового обслуживания приведена на рис.5.

Теория экспоненциальных СеМО наиболее разработана, и ее широко применяют, как для исследования сетей передачи данных, так и для исследования мультипроцессорных вычислительных систем. Разработаны практические формы расчета вероятностно-временных характеристик таких сетей и систем.

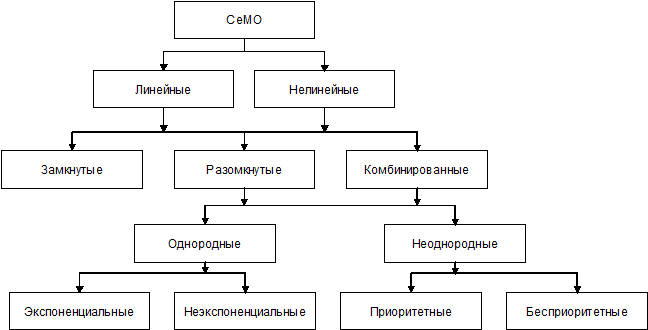
Рис. Классификация сетей массового обслуживания

Система массового обслуживания M/M/1

При рассмотрении системы массового обслуживания M/M/1 для стационарных вероятностей

,

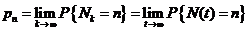при любых 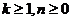в течение времени от 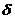(малое положительное число) до 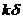общее число переходов из состояния п в п+1 должно отличаться от общего числа переходов из п+1 в п не более чем на 1.

В стационарном режиме вероятность того, что система находится в состоянии п и при следующем переходе попадает в состояние п+1, равна вероятности того, что система находится в состоянии п+1 и делает переход в состояние п:

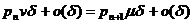
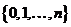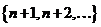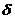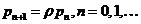Эти уравнения называются уравнениями глобального баланса, соответствующие множеству состояний и с точностью до о(d). Так как не зависит от и устремляя в (3.10), можно получить , где 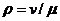, - скорость обслуживания (число запросов, обслуживаемых в единицу времени).

Используя уравнения глобального баланса:

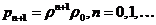
и если 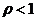(скорость обслуживания превышает скорость поступлений), все вероятности являются положительными, а сумма их равна единице, тогда:

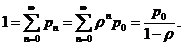
Это соотношение вместе с формулой (3.11) дает:

.

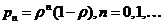Таким образом, среднее число запросов в системе в стационарном режиме вычисляется по формуле

,

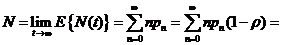
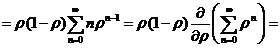
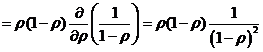а, используя равенство 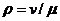можно получить, что:

.

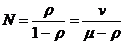В терминах системы пакетной передачи 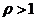означает, что vl>SP_кан, где v - скорость поступления, l - средняя длина пакета в битах, SP_кан - пропускная способность канала в битах в секунду.

Средняя задержка в системе (время ожидания запроса в очереди плюс время обслуживания), согласно теореме Литтла, равна

t_{з.ср .=} .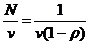

Подставляя 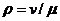, получится:

t_з.ср = 1/ (m - v).

Среднее время ожидания в очереди t_ож равно средней задержке минус среднее время обслуживания запроса , поэтому:

t_ож = .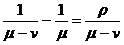

Для системы пакетной передачи, в которой скорость поступления (в пакетах в секунду) увеличивается от v, до Kv, где K — некоторый числовой коэффициент, распределение длины пакетов остается неизменным, а пропускная способность возрастает в K раз, так что среднее время передачи пакета становится равным 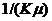вместо . Следовательно, коэффициент использования линии r и среднее число пакетов в системе остаются неизменными:

.

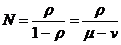Однако, средняя задержка пакета будет равна t_з.ср =N/Kv и уменьшится в К раз. Линия передачи данных, которая передает в К раз быстрее, будет передавать в К, раз больше пакетов в секунду со средней задержкой пакета в К раз меньшей. Этот общий результат применим и к компьютерным корпоративным сетям. Таким образом, когда пакет поступает в сеть, он обнаруживает перед собой в вероятностном смысле такое же число пакетов, как и в случае низкоскоростной линии передачи, но пакеты, стоящие впереди него, будут продвигаться в К раз быстрее.

Пусть n статистически одинаковых и независимых пуассоновских потоков пакетов передаются по линии связи со скоростью /n пакетов в секунду каждый. Длины пакетов во всех потоках независимы и имеют экспоненциальное распределение. Среднее время передачи равно . Если потоки сливаются в один пуассоновский поток с интенсивностью , как это происходит при статистическом уплотнении, средняя задержка пакета становится равной:

t_з.ср =1/( - ).

Если пропускная способность канала делится на n равных частей, по одной для каждого потока пакетов, как при временном или частотном уплотнении, то каждая часть ведет себя как система массового обслуживания M/M/1 со скоростью поступления /n и средней скоростью обслуживания /n. Следовательно, средняя задержка пакета равна t_з.ср = 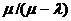, т.е. в n раз больше, чем при статистическом уплотнении.

Из этого следует, что уплотнение большого числа потоков путем распределения их по отдельным каналам линии передачи является очень неэффективным в смысле задержки. Эффективность сети становится хуже, если пропускная способность каналов распределяется не прямо пропорционально интенсивностям соответствующих потоков.