Алгоритм генерации гауссовской случайной величины

Алгоритм реализует генерацию значений гауссовской стандартной величины (ГСВ)ξ, имеющей параметры

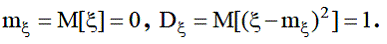
Работа алгоритма основывается на результатах центральной предельной теоремы, согласно которой суммаn значений одинаково распределенных и независимых случайных величин имеет в пределе (приn →∞)гауссовское распределение.

Имея датчик РСВ, значение ξ может быть получено как

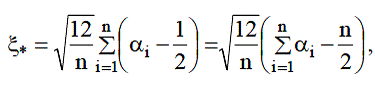
где αi – независимые значения равномерной случайной величины α, получаемые при последовательных обращениях к датчику РСВ. Величину n достаточно выбирать порядка 10...20. В вычислительном отношении удобно выбирать n = 12 , тогда получается простейший алгоритм генерации ГСВ

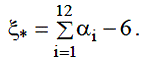
9.Моделирование случайных величин с произвольным законом распределения (1,2,3).

Метод нелинейного функционального преобразования.Особенностью данного метода является то, что он может использоваться для генерации величин, заданных аналитическим видом закона распределения.

Теорема.

Пустьслучайная величинаαимеет равномерное распределение винтервале [0, 1]и связана со случайной величиной ξ соотношением

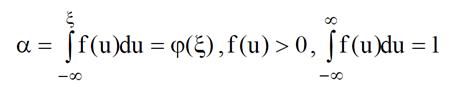
где f (u) – некоторая функция, удовлетворяющая указанным свойствам.

Тогдаслучайная величинаξимеет плотность распределения вероятностей вида f (u) и может быть найдена на основе обратного функционального преобразования

Для доказательства найдем функцию распределения ξ. Используем тот факт, что при f (u) > 0 величинаα монотонно возрастающая функция ξ.

Также и ξ в этом случае монотонно возрастающая функция α. Тогда для функции распределения ξ выполняется следующая цепочка равенств:

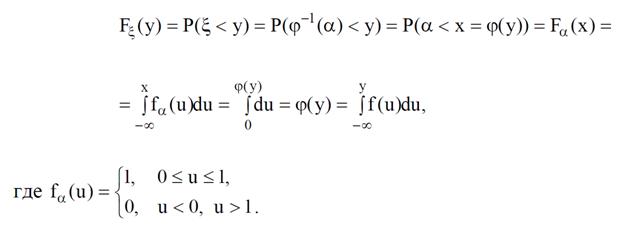
Очевидно, что Fξ(y) = ϕ(y) , что и требовалось доказать, так как это
означает, что ξ имеет плотность распределения вида f (u)(fξ(u) = f (u)).
Таким образом,последовательность случайных чиселξiс таким
распределением можно получить из соотношения вида

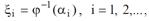где α_i− последовательность значений РСВ, получаемых при обращении к датчику α.

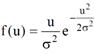Пример. Пусть− закон Релея. Тогда

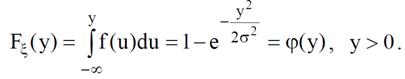Функциональная связь величин ξ и α определяется соотношением

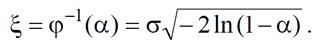
При непосредственной генерации можно использовать более экономное соотношение

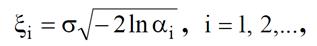
так как величина 1−α также имеет равномерное распределение на интервале [0, 1].

Метод исключений (метод Фон-Неймана).Особенностью данногометода является то, что он может использоваться для генерации величин, заданных как аналитическим видом закона распределения, так и эмпирически полученными распределениями.

Теорема.

Пустьфункцияg(x)≥0и на ее основе определено множество значений вещественных переменных G ={(x, y), 0 ≤ y ≤ g(x)}.

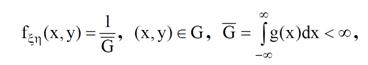
Пустьсовместная плотность распределения случайных величинξиη на множестве значений G равна

то есть имеет равномерный вид.

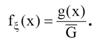Тогдаплотность распределения вероятностей случайной величиныξ равна

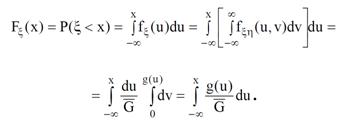Учтем, что для функции распределения ξ выполняется

Отсюда следует доказательство теоремы, так как
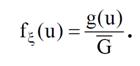