Геометрических фигур методом Монте-Карло

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ РАБОТ ПО ДИСЦИПЛИНЕ

“МОДЕЛИРОВАНИЕ СИСТЕМ”

Донецк,

ГВУЗ “ДонНТУ” 2011

Министерство образования и науки Украины

Донецкий национальный технический университет

Кафедра компьютерных систем мониторинга

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ РАБОТ ПО ДИСЦИПЛИНЕ

“МОДЕЛИРОВАНИЕ СИСТЕМ”

Часть 2

(для студентов специальности 7.080407

«Компьютерный эколого-экономический мониторинг»,

«Программирование медиасистем и компьютерный дизайн»)

Рассмотрены на заседании

кафедры Компьютерных

систем мониторинга

Направление подготовки – 0804 “Компьютерные науки”

Протокол № 6 от «11» февраля 2011 г.

Утверждено на заседании

учебно-издательского совета

Протокол № __ от «__» ____________ 2011 г.

УДК 502.5:004.358(076.5)

Методические указания к выполнению лабораторных работ по дисциплине “Моделирование систем”, часть 2 (для студентов специальности 7.080407 «Компьютерный эколого-экономический мониторинг», «Программирование медиасистем и компьютерный дизайн»).

Составители: д.т.н., проф. Аверин Г.В., к.т.н., доц. Звягинцева А.В. – Донецк: ДонНТУ, 2011. – 74 с.

Составители: д.т.н., проф. Аверин Г.В.

к.т.н., доц. Звягинцева А.В.

© Кафедра КСМ, ГВУЗ “ДонНТУ”

Лабораторная работа № 1

Определение площади

Геометрических фигур методом Монте-Карло

Цель работы: получение навыков проведения статистических экспериментов

Общие положення

Имитационная модель – это формальное (то есть выполненное на некотором формальном языке) описание логики функционирования исследуемой системы и взаимодействия отдельных ее элементов во времени, учитывающее наиболее существенные причинно-следственные связи, присущие системе, и обеспечивающее проведение статистических экспериментов.

В результате имитационных экспериментов исследователь получает набор экспериментальных данных, на основе которых могут быть оценены характеристики системы.

Иммитационная модель должна отвечать двум основным требованиям:

– отражать логику функционирования исследуемой системы во времени;

– обеспечивать возможность проведения статистического эксперимента.

В основе статистического эксперимента лежит метод статистических испытаний (метод Монте-Карло). Суть его состоит в том, что результат испытания ставится в зависимость от значения некоторой случайной величины, распределенной по заданному закону. Поэтому результат каждого отдельного испытания также носит случайный характер.

Проведя серию испытаний, получают множество частных значений наблюдаемой характеристики (то есть выборку). Полученные статистические данные обрабатываются и представляются в виде соответствующих численных оценок интересующих исследователя величин (характеристик системы).

Теоретической основой метода статистических испытаний являются предельные теоремы теории вероятностей (теорема Чебышева, теорема Бернулли, теорема Пуассона). Принципиальное значение предельных теорем состоит в том, что они гарантируют высокое качество статистических оценок при весьма большом числе испытаний.

Важно отметить, что метод статистических испытаний применим для исследования как стохастических, так и детерминированных систем.

Еще одной важной особенностью данного метода является то, что его реализация практически невозможна без использования ЭВМ.

В качестве иллюстрации к изложенному рассмотрим применение метода статистических испытаний для вычисления площади круга заданного радиуса. Данная задача относится к классу детерминированных, поскольку весьма сложно представить себе случайные факторы, под влиянием которых площадь неподвижной геометрической фигуры могла бы изменяться.

Пусть круг имеет радиус r = 5, и его центр находится в точке с координатами О(1, 2). Уравнение соответствующей окружности имеет вид:

(x – 1)² + (y – 2)² = 25. (1.1)

Для решения задачи методом Монте-Карло опишем вокруг круга квадрат. Его вершины будут иметь координаты (-4, -3), (6, -3), (-4, 7) и (6, 7). Координаты любой точки, лежащей внутри квадрата или на его границе должны удовлетворять неравенствам: -4 < х < 6 и -3 < у < 7. Квадрат будет иметь длину ребра, равную 10.

При решении данной задачи естественно исходить из того, что все точки в этом квадрате могут появляться с одинаковой вероятностью, то есть будем считать, что х и у распределены равномерно с плотностями вероятностии:

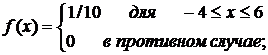(1.2)

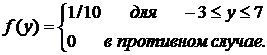(1.3)

Проведя некоторое количество испытаний (то есть получив множество случайных точек, принадлежащих квадрату), подсчитаем число точек, попавших внутрь круга или на окружность. Если выборка состоит из n наблюдений и из n точек m точек попали внутрь круга или на окружность, то оценку площади круга можно получить из соотношения:

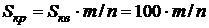. (1.4)

В таблице приведены оценки площади круга 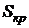, полученные для разных значений n, причем для каждого n выполнялось 5 прогонов (точное значение 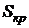= 78,54 см):

Прогоны отличаются друг от друга последовательностями случайных чисел, из которых формировались координаты точек.

На основании полученных результатов могут быть сделаны выводы, которые справедливы для любого имитационного эксперимента независимо от физической природы и типа моделируемой системы:

– каждый прогон модели можно рассматривать как одно наблюдение в проводимом эксперименте на модели;

– с увеличением продолжительности прогона (то есть продолжительности наблюдения) отклонение измеряемой величины от ее точного значения уменьшается, поскольку наблюдаемая система переходит в стационарное состояние;

– влияние переходных условий можно уменьшить, если увеличить количество прогонов модели (то есть количество экспериментов);

– существует предел, за которым увеличение продолжительности прогона модели уже не дает существенного повышения точности результата, измеряемой дисперсией.

Таблица 2.1. – Результаты оценки площади круга методом статических испытаний

Номер прогона	Оценки площади круга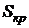
Число испытаний (n)
		1 000	5 000	10 000
		79,5		79,5
				78,88	78,8
		77,3	80,2	79,5	79,8
		79,12	71,29	78,22	78,6
		77,72	77,76		78,26
среднее	75,6	78,13	76,85	79,02	78,79
дисперсия	27,3	1,248	11,077	0,280	1,024

Основная цель рассмотренного примера – привлечь внимание к тому факту, что имитационное моделирование не ограничивается разработкой модели и написанием соответствующей программы, а требует подготовки и проведения статистического эксперимента. В связи с этим результаты имитационного моделирования следует рассматривать как экспериментальные данные, требующие специальной обработки и анализа.

Задание

Используя метод Монте-Карло определить площадь геометрической фигуры. Найти среднее и дисперсию экспериментальных данных по значениям площади. Сравнить значения полученной площади фигуры с её точным значением, используя для этого математические формулы.

Таблица 1.7 – Варианты заданий

№ ва-рианта	Вид фигуры
А	В	С	D
	Нижняя часть фигуры, образованная окружностью радиуса 2 и кубической параболой	эллипс с центром в начале координат с полуосями а=1, в=2	Сегмент, образованный окружностью с центром в начале координат радиусом 2 и прямой, проходящей через точки А(2, 0), В(0, 2)	Фигура, образованная параболой у=х2 и прямыми у=0 и х=2
	Фигура, образованная окружностью радиусом 1, параболой у=x2 и прямой y=0	Фигура, образованная окружностью радиусом 1 и параболой у=x2	Фигура, образованная параболой у=2x2, гиперболой y=1/x и прямыми у=0 и х=2	Первая полувол-на синусоиды у=sin x
	Фигура, образованная первой полувол-ной синусоиды у=sin x, функцией у=соsx и прямой х=0	Кольцо с центром в начале координат и радиусом 2 и 1.	Эллипс с центром в начале координат с полуосями а=1, в=2 и вырезанный круг с радиусом 1.	Круг радиуса 1с вырезанным треугольником с вершинами А(-0,5, 0), В(0,5, 0) С(0, 1)
	Треугольник с координатами вершин А (1,1), В (2, -2), С (-1, -1) с отверстием в виде вписанной окружности	Фигура, образованная окружностью радиусом 1 и вписанным в него квадратом	Фигура, образованная первой полуволной синусоиды у=sinx и y sin=2x	Фигура, образованная окружностью радиуса 1 с центром в начале координат и окружностью радиуса 0,5 с центром в точке А(0, 0,5)
	Объем сферы радиуса 2	Объем цилиндра диаметра 2 и высотой 1.	Объем конуса с диаметром основания 2 и высотой 2.	Площадь поверхности цилиндра диаметра 2 и высотой 1.
	Площадь под кривой, характеризующей плотность нормального распределения со средним, равным 0 и дисперсией 1.	Площадь поверхности пирамиды с квадратным основанием, стороной 1 и высотой 1	Площадь поверхности конуса с диаметром основания 2 и высотой 2.	Площадь под кривой еxp(-x2)

1.6 Рекомендуемая литература

1. Гультяев А. Имитационное моделирование в среде Windows. Практическое пособие. – СПб.: Корона-принт, 1999.-288с.

2. Максимей И.В. Имитационное моделирование на ЭВМ. М.: Радио и связь, 1988.

3. Технология системного моделирования/Под ред. С.В. Емельянова, В.В. Калашникова и др. М.: Машиностроение; Берлин: Техник, 1988.

4. Советов Б.Я., Яковлев С.А. Моделирование систем. 2-е издание, перераб. и доп. М.: Высшая школа, 1998.

1.7 Контрольные вопросы

1. Охарактеризовать методику проведения статистического эксперимента.

2. Расписать метод статистических испытаний (метод Монте-Карло).

3. Как зависит точность эксперимента от количества прогонов модели.

4. В каких случаях целесообразно применять имитационное моделирование.

Преимущества и недостатки использования имитационного моделирования.
Лабораторная работа № 2

Порядок выполнения работы

1. Изучить согласно варианту особенности объекта (явления), установить его природу, построить описательную модель и указать основные принципы и особенности его моделирования.

2. Дать характеристику условий формирования, функционирования, особенностей поведения, эволюции системы и т.д. Расписать наиболее существенные факторы (с указанием диапазонов их изменения), влияющие на его формирование и дальнейшее развитие (угасание).

а) для группы ПКД – графического образа объекта (явления) с использованием 3ds max, photoshop, Adobe Flash, HTML5, Illustrator, Corel, CorelDraw, AutoCAD и т.п.

Изучить графический образ объекта и явления. Построить простейшую структурную модель объекта на основе линий, окружностей, овалов, точек и т.д. Предложить способы описания данного графического объекта геометрическими уравнениями. Например, линии: 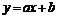; окружности: 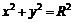, крупной точки 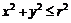и т.д.

Предложить способы нанесения формы, цвета, теней и т.д. на простейшие геометрические объекты.

Предусмотреть возможность анимации и движения данного объекта (явления) во времени (пространстве).

Описать возможный алгоритм перемещения объекта. Результаты работы оформить в виде словесного алгоритма (блок-схемы) и динамической картинки изображения на компьютере.

б) для группы КЭМ – абстрактной модели с использованием Statistica, Matlab и Simulink, MathCAD, Delphi, C++, C Sharp и т.п.

Построение простейшей математической модели объекта, например, модель физического маятника следует основывать на уравнении колебаний; моделирование преломления света в линзе – с учетом уравнений оптики; подпрыгивание мяча – используя уравнения кинематики; биение сердца – на основе экспериментальных данных о изменении сердечного ритма; нашествия саранчи – путем оценки случайного перемещения объекта к источнику пищи; перетаскивания гусеницы – путем определения равнодействующей действующих сил и т.д.

3.1 Построение статистического образа.

3.2 На его основе сделать

а) динамическую анимацию, визуализацию движения объекта в пространстве и времени (для группы ПКД);

б)

3.1. Построить простейшую математическую (имитационную, статистическую, стохастическую, детерминированную и т.п.) модель объекта (КЭМ).

3.2 Осуществить анализ поведения объекта моделирования.

3. С использованием презентационных средств Power Point или flash подготовить доклад о проделанной работе продолжительностью 5 – 7 минут. Обработанный материал представить в виде отчета, в приложениях которого поместить текст доклада и презентацию. К бумажному отчету приложить магнитный носитель с записью электронного варианта самого отчета (реферата), доклада и презентации к нему.

Варианты заданий

Пользуясь литературой и источниками Интернет, осуществить поиск информации по одной из нижеперечисленных тем согласно варианту задания. Обработанный материал представить в виде отчета о проделанной работе и подготовить соответствующий доклад с использованием презентационных средств. Список тем для поиска информации представлен в таблице 1.1.

Таблица 1.1. – Перечень тем для поиска, обработки и систематизации информации

Для группы ПКД	Для группы КЭМ
Вариант	объект (явление, процесс)	Вариант	объект (явление, процесс)
	Природные объекты (явления):		Физические системы:
	молния		маятник
	прибой		часы с кукушкой
	гроза		движение жидкости в сужающейся трубке
	возгорание и распространение огня (пожар)		подпрыгивание мяча
	капель (таяние снега весной)		выстрел снаряда под углом
	паводки-половодье-наводнение (и межень). Структура поверхности реки при её обмелении и поднятия уровня воды		гравитационная система “Земля-Луна”
	снежинка		обращение спутника вокруг Земли
	иней в виде рисунка на окне		преломление света в линзе
	солнечное затмение		движение тела по горке “Мертвая петля” (“Чертова петля”)
	образование и исчезновение радуги		движение подводной лодки под водой и её всплывание
	северное сияние		процесс горения лампочки от батарейки
	образование и исчезновение тумана		полет “Бумажного змея”
	кольца Сатурна		вращающийся “волчок”
	вихри		пружинные весы - кантер
	галактики		качели
	шторм		компас
	образование пустыни (засуха)		парашют
	горная гряда		передача звука. Колокол
	выпадение и окончание дождя		бинокль
	стоки рек		таяние кубика льда в стакане воды
	рельеф и береговые линии		поведение дольки шоколада в бакалее шампанского
	изморозь на траве		чашечные весы
	падение метеоритов		модель состояния газа в баллоне
	снеговая лавина		вода при подъеме в капиллярах разных диаметров
	колебания уровня воды в водоемах		модель “Барометр Гетте”
	буря (торнадо)		передача тепла через стенку
	штормовые волны		воздушный шар (подъем, полет, опускание)
	извержение вулканов		солнечные часы
	град		Биологические и экологические системы:
	тайфуны		процесс роста подснежника
	метель		процесс цветения воды
	наводнение		модель “Хищник-жертва”
			процесс перетаскивания гусеницы муравьями
	отражение объектов в реке (“Мир из-под воды”)		процесс поиска меда пчелой
	звездное небо		движение крови по сосудам
	фазы луны (полнолуние, молодой месяц и т.д.)		биение сердца
	восход и заход солнца		колебание дерева на ветру
	протуберанцы на солнце		планирование птицы
	водопад		нашествие саранчи
	рост кристаллов		Чрезвычайные ситуации и опасные явления:
	метеоритный дождь		наводнение
	Техногенные системы и изобретения человека:		засуха
	“переливание” на свету разлитой нефти (масла)		метель
	цветомузыка		ураган
	калейдоскоп		изменение климата на Земле
	построение рисунка спичками		загрязнение реки
	динамические заставки Windows (плавающие рыбки, падающий снег и т.д., их периодическая смена)		лесной пожар
	нанотехнологии		землетрясение
	глобус		Социально-экономические системы:
	вязание узора одной нитью		рост численности населения
	сборка кубика-рубика (головоломка, пятнашка)		динамика курса доллара
	озерные ландшафты, водохранилища		динамика изменения потребления энергии и выброс парниковых газов
	горизонт		оценка потенциала человеческого развития
	броуновское движение газа в цилиндре с поршнем		распространение эпидемии
	Биологические системы:		заболеваемость населения
	набухание почек		Информационные системы:
	бабочка		процесс записи информации на винчестер
			процесс считывания музыки с медиаплеера
	рост грибов		модель сети Интернет
	рост ветвей деревьев (пределы роста, засыхание ветвей, вид крон деревьев)		хранение информации в оперативной памяти
	рост цветка во времени, его распускание и увядание (в сжатом (ускоренном) промежутке времени)		модели передачи информации через Интернет-почту
	ДНК		моделирование процесса набора информации на клавиатуре
	геометрия артерий и вен. Кровообращение		модель работы устройства “мышь”
	бронхи		модель считывания информации при сканировании
	Фантастические рисунки:		модель вывода информации на ксерокс
	подводный мир		Химические системы:
	НЛО		процесс горения углеродного топлива
	футбол роботов		процесс горения дымного пороха
	водяная планета		хлорирование воды
	огненная планета		взаимодействие соляной кислоты с раствором хлорида натрия
	дизайн машины будущего		каталитическое окисление аммиака кислородом воздуха – “Огненная метель”
	машина времени		получение кислорода из перманганата калия
	мир разумных кристаллов		получение водорода в лаборатории
			гашение извести
			вытеснение кислорода из воды хлором
	космические станции		покрытие металлических предметов никелем и золотом
	Винни-Пух		периодическая система Менделеева
	заяц и волк (из мультфильма “Ну погоди!”)		модель атома
	Дюймовочка и крот		модель молекул
	полет в поясе астероидов		Техногенные системы и изобретения человека:
	Стиль живописи и абстрактные рисунки:		игра в бильярд
	живопись Китая		игра в боулинг
	живопись эпохи Возрождения		система управления холодильником
	живопись эпохи Просвещения		стабилизатор напряжения
	живопись эпохи Барокко		источник бесперебойного питания
	живопись эпохи Классицизма		модель ртутного градусника
	живопись эпохи Романтизма		фейерверк
	живопись эпохи Палеолита		модель “светофор” (с дополнительной стрелкой, ручного управления, обычный)
	живопись эпохи Мезолита		аэрозольный баллончик
	абстрактные рисунки		модель сливного бочка
	икебана		работа и конструкция ледокола

Требования к заданию.

1.2 Рекомендуемая литература

1. Б. Мандельброд. Фрактальная геометрия природы. Пер. с англ. А.Р. Логунова. М.: Институт компьютерных исследований. 2002. 666 с.

2. Я.И. Перельман. Занимательная физика. Книга 1. М.: Наука, 1979. – 126 с.

3. Я.И. Перельман. Занимательная физика. Книга 2. М.: Наука, 1983. – 153 с.

4. Я.И. Перельман. Знаете ли вы физику? М: Наука, 1992. – 275 с.

5. Я.И. Перельман. Занимательные задачи и опыты. 1959. –529 с.

6. Я.И. Перельман. Занимательная астрономия. М.: Технико-теоретическая литература, 1954. – 212 с.

7. Занимательная биология и химия найти

8. Я.И. Перельман. Занимательная математика. Ленинград.: Время, 1927. – 97 с.

9. Я.И. Перельман. Занимательная алгебра. М.: Наука, 1967. – 200 с.

10. Я.И. Перельман. Живая математика. М.: Наука, 1967. – 160 с.

11. Гультяев А.К. MATLAB 5.2. Имитационное моделирование в среде Windows: Практическое пособие. – 286 с.

12. Тудор Оприш. Занимательная бионика. Бухарест: Альбатрос., 1986. – 163 с.

13. Л.В. Тарасов. Физика в природе. М.: Просвещение, 1988. – 351 с.

Лабораторная работа №3

Вероятностные модели

Общие положения

В основу многих вероятностных моделей процессов и явлений могут быть положены законы распределения случайных величин. Например, известно, что относительная частота рождений младенцев мужского пола заметно не отличается от значения 0,515, если учтено достаточно большое число рождений. Эта частота не зависит от местности, где проводятся наблюдения, или от этнического состава населения. В свою очередь, если определять относительную частоту распада изотопа радия 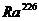за 100 лет, то всегда будет получаться величина 0,04184.

Для очень многих событий установлены те или иные законы распределений. Например, распределение Пуассона применяют при исследовании рисков отказов оборудования, возникновения пожаров, производственных аварий, природных катастроф типа тайфунов, смерчей; распределения Вейбулла, Парето – при исследовании землетрясений, наводнений, извержений вулканов, крупных техногенных катастроф, катастрофических пожаров; гамма-распределение – при изучении риска смертельного травматизма, числа промышленных аварий и т.д.

В физике имеется масса примеров, которые связаны с оценкой состояния физических систем на основе определения вероятности событий, свойственных данным системам. Известно, что значения скоростей молекул подчиняются распределению Максвелла, ошибки наблюдений – нормальному распределению, случайные блуждания частиц – распределению арксинуса, сила притяжения (отталкивания), действующая на частицу газа, который представляет собой совокупность заряженных ионов – распределению Хольцмарка и т.д.

В системах телекоммуникаций замирания в канале связи при отсутствии прямой видимости между абонентом и базовой станцией имеют рэлеевский закон распределения; аддитивные помехи (шумы) часто описываются нормальным (гауссовским) законом распределения; временные интервалы между вызовами в телефонных сетях связи обычно имеют экспоненциальный закон распределения.

На практике часто приходится выбирать вид модельного распределения не имея достаточного объема данных, чтобы можно было бы проверить его адекватность. Выбор вида распределения обычно основывается на прошлом опыте, на знании механизма конкретного явления или на теоретических предпосылках.

Краткие сведения о распределениях вероятностей случайных величин

Известно, что основной вероятностной характеристикой случайных величин является плотность распределения вероятности. Для различных вероятностных распределений зависимости для определения плотности вероятности имеют вид:

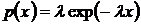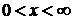, – для показательного закона распределения;

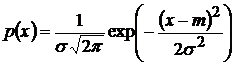– для нормального (гауссова) закона распределения;

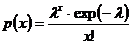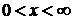, – для пуассоновского закона распределения;

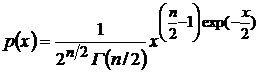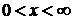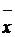
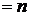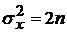, , , – для закона распределения хи-квадрат (частный случай при 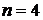– рэлеевское распределение - ;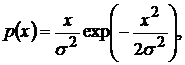

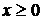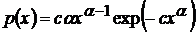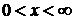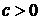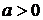, , , – для закона распределения Вейбулла;

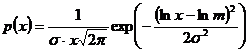– для логнормального закона распределения;

Источники случайных чисел

Физические источники настоящих случайных чисел не отличаются многообразием. Шумы, такие как детекторы событий ионизирующей радиации, дробовой шум в резисторе или космическое излучение могут быть источниками случайных чисел. Однако устройства, использующие эти явления, применяются редко. Более простым решением является создание некоторого набора из большого количества случайных чисел и опубликование его в некотором словаре в таблицах. Однако такие наборы обеспечивают ограничительные последовательности случайных чисел по сравнению с тем количеством, которое требуется на практических приложений.

Чаще всего используют для генерации случайных чисел различные алгоритмы. Эти алгоритмы заранее определены и, следовательно, генерируют последовательность чисел, которая теоретически не может быть статистически случайной. В то же время, если выбрать хороший алгоритм, полученная численная последовательность будет удовлетворять большинству тестов на случайность. Числа, генерируемые алгоритмами и удовлетворяющие статистическим критериям, называют псевдослучайными числами.

В основе моделирования случайных величин лежат методы имитационных случайных чисел с помощью генераторов.

Очевидно, что абсолютно случайные числа нельзя получить, используя определённый алгоритм. Однако можно создать такую последовательность чисел, которая будет обладать многими свойствами случайных чисел. Такие числа называются псевдослучайными. Впервые способы создания псевдослучайных чисел предложил Джон фон Нейман в 1946 г.

Генератор псевдослучайных чисел (ГПСЧ) представляет собой алгоритм, генерирующий некоторую последовательность чисел, которые почти независимы друг от друга и подчиняются заданному вероятностному распределению (обычно равномерному).

Современная информатика широко использует псевдослучайные числа в самых разных приложениях: в методе Монте-Карло, при имитационном моделировании, в криптографии и т.д. При этом от качества применяемых ГПСЧ напрямую зависит качество получаемых результатов.

Детерминированные ГПСЧ

Детерминированный алгоритм не может генерировать абсолютно случайные числа, он может только генерировать последовательность с некоторыми случайными свойствами.

Для создания таких алгоритмов используют различные методы, например, линейный конгруэнтный метод, метод Фибоначчи с запаздываниями, регистр сдвига с линейной обратной связью, регистр сдвига с обобщенной обратной связью.

Из современных ГПСЧ широкое распространение также получил алгоритм «вихрь Мерсенна», предложенный в 1997 году Мацумото и Нисимурой и основанных на свойствах простых чисел Мерсенна. Его достоинствами являются колоссальный период (2¹⁹⁹³⁷ − 1), равномерное распределение в 623 измерениях, быстрая генерация случайных чисел (в 2-3 раза быстрее, чем другие ГПСЧ). Однако, существуют алгоритмы, распознающие последовательность, порождаемую вихрем Мерсенна, как неслучайную.

Варианты заданий

Ва- ри- ант	Виды законов распределений случайных сигналов
Показа- тельный	Нормальный	Рэлеев- ский	Вейбула	Периодический сигнал
	+	+, m=2;s=1	–	+	синусоидальный
	+	+, m=0;s=2	+	–	косинусоидальный
	–	+, m=5;s=4	+	+	ступеньчатый
		+, m=3;s=2,5	–		П-образный
	+	+, m=7;s=3	+	–	из равносторонних треугольников, имеющих общую точку соприкосновения
	+	+, m=10;s=7	–	+	из полукругов
	+	+, m=4;s=3	+	–	пила в виде прямоугольных трапеций
	+	+, m=0;s=3	–	+	пила в виде прямоугольных треугольников с гипотенузой справа
	–	+, m=5;s=7	+	+	пила из парабол и прямых линий
	–	+, m=2,5;s=2	+	+	сигнал из косинусоиды по модулю
	–	+, m=2;s=1,8	+	+	сигнал из равнобедренных треугольников, перекрывающих друг друга (холмы)
	+	+, m=3;s=1,5	–	+	пила в виде прямоугольных треугольников с гипотенузой слева
	+	+, m=0;s=3	+	–	сигнал “хоккейная клюшка”
	–	+, m=5;s=4	+	+	сигнал в виде отдельных отрезков под углом 45° (слеш)
	+	+, m=3;s=2,8	+	–	S-образный сигнал
	–	+, m=0;s=5	+	+	Сигнал из накладывающихся друг на друга перевернутых восьмерок
	+	+, m=7;s=4,5	–	+	сигнал из равнобедренных трапеций
	+	+, m=0;s=5	+	–	X-образный сигнал (сигнал “ромбики”)
	–	+, m=7;s=3	+	+	Сигнал растянутой спирали
	+	+, m=2;s=1	–	+	Сигнал “перекрывающиеся кольца”

Контрольные вопросы:

1. Какими способами можно получить случайный процесс с экспоненциальным распределением?

2. Какими способами можно получить случайный процесс с рэлеевским распределением?

3. Как можно оценить математическое ожидание и дисперсию случайной величины по соответствующим графикам плотности распределения вероятностей?

4. Какова связь между средним квадратом и дисперсией случайной величины?

5. Каким образом можно найти математическое ожидание случайной величины, зная её плотность распределения вероятностей?

6. Каким образом можно найти средний квадрат случайной величины, зная её плотность распределения вероятностей?

7. Как определить по графику плотности распределения вероятностей вероятность попадания случайной величины в заданный промежуток её значений?

8. Какие реальные случайные процессы имеют нормальное (гауссово) распределение, рэлеевское распределение, равномерное распределение, распределение Пуассона?

9. Каковы основные характеристики генератора случайных чисел в ЭВМ: закон распределения, интервал изменения случайных чисел?

10. В чем заключается центральная предельная теорема теории вероятностей?

11. Каковы характерные особенности модели белого шума?

1.2 Рекомендуемая литература

1. Е.И. Гурский Теория вероятностей с элементами математической статистики: уч. пос. для вузов / Е.И. Гурский. – М.: Вс. шк., 1971. – 328 с.

2. Дж. Купер. Вероятностные методы анализа сигналов и систем / Дж. Купер, К. Макгиллем; пер. с англ. В.Т. Горяинова. – М.: Мир, 1989. – 376 с.

3. В.П. Бакалов. Цифровое моделирование случайных процессов / В.П. Бакалов. – М.: Сайнс-пресс, 2002. – 88 с. – (Серия «Конспекты лекций по радиотехническим дисциплинам» ; вып. 4).

4. Боровиков В. STATISTICA для профессионалов. СПб.: Питер. 2001. – 655 с.

5. Гультяев А.К. Matlab 5.2. Имитационное моделирование в среде Windows: практическое пособие.

Лабораторная работа №4

Общие положения

Под потоком событий в теории случайных процессов понимается последовательность событий, происходящих одно за другим в какие-то моменты времени. Примерами могут служить: поток вызовов на телефонной станции; поток включений приборов в бытовой электросети; поток заказных писем, поступающих в почтовое отделение; поток сбоев (неисправностей) персонального компьютера; поток выстрелов, направляемых на цель во время стрельб и т.п. События, образующие поток, в общем случае могут быть различными, но чаще всего рассматривают потоки однородных событий, различающихся только моментами появления во времени.

Рассмотрим потоки событий, обладающие некоторыми особенно простыми свойствами. Сред