Анализ систем в частотной области.

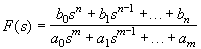
Изображение полюсов и нулей функции цепи F(s) на комплексной плоскости позволяет наглядно проследить за характером частотных зависимостей модуля и аргумента комплексной функцииF(jw) — ее амплитудно- и фазочастотной характеристиками — во всем частотном диапазоне w (от нуля до бесконечности). Отдельные сомножители полиномов числителя и знаменателя F(s) (22.1) (s – s_0k) и (s – s'_0k) при s = jw изображаются на комплексной плоскости векторами, направленными из точек расположения полюсов и нулей в точку мнимой оси, соответствующую данной частоте w (рис. 22.3).

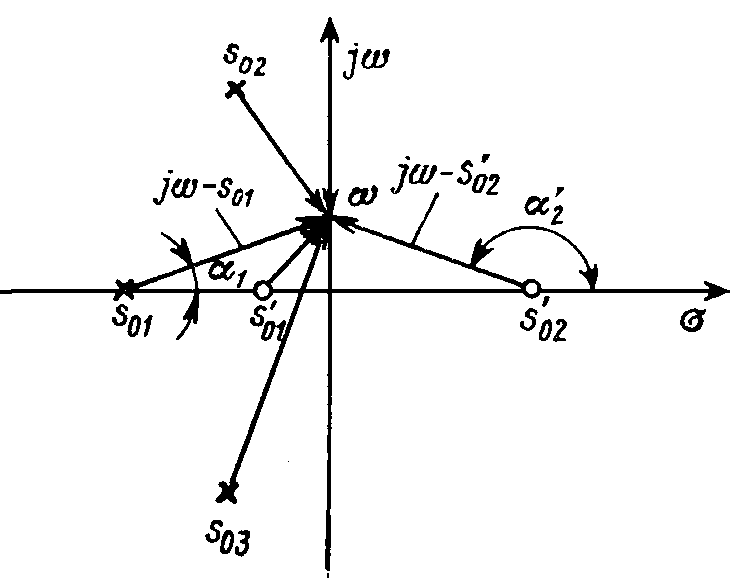
Модуль функции F(jw) представляется отношением произведения модулей векторов jw – s'_0k, отвечающих нулям функции F(s), к произведению модулей векторов jw – s_0k, соответствующих ее полюсам. Аргумент F(jw) аналогично определяется разностью суммы аргументов a'_k векторов jw – s'_0k и суммы аргументов a_k векторов jw – s_0k (см. рис. 22.3).

Так, вещественным полюсам и нулям с ростом частоты соответствует монотонное увеличение модулей отдельных сомножителей jw – s_0k и монотонное увеличение аргумента от 0 при w = 0 доp /2 при w = ¥. Для комплексного полюса или нуля s_0k = d_0k + jw_0k изменение модуля сомножителя имеет немонотонный характер — в точке оси w = w_0k, ближайшей к данной особой точке, модуль принимает минимальное значение, равное ½d_0k½. Это определяет заметные изменения модуля и фазы вблизи соответствующего полюса и нуля. Чем ближе полюс или нуль к мнимой оси, тем резче выражены изменения амплитудно- и фазочастотной характеристики в его окрестности.

Передаточные функции цепей с симметричным относительно мнимой оси расположением всех нулей и полюсов (например, рис. 22.2, б) имеют постоянный модуль при всех значениях w.

Рассмотрим два четырехполюсника, изображенных на рис. 22.4, а,б.

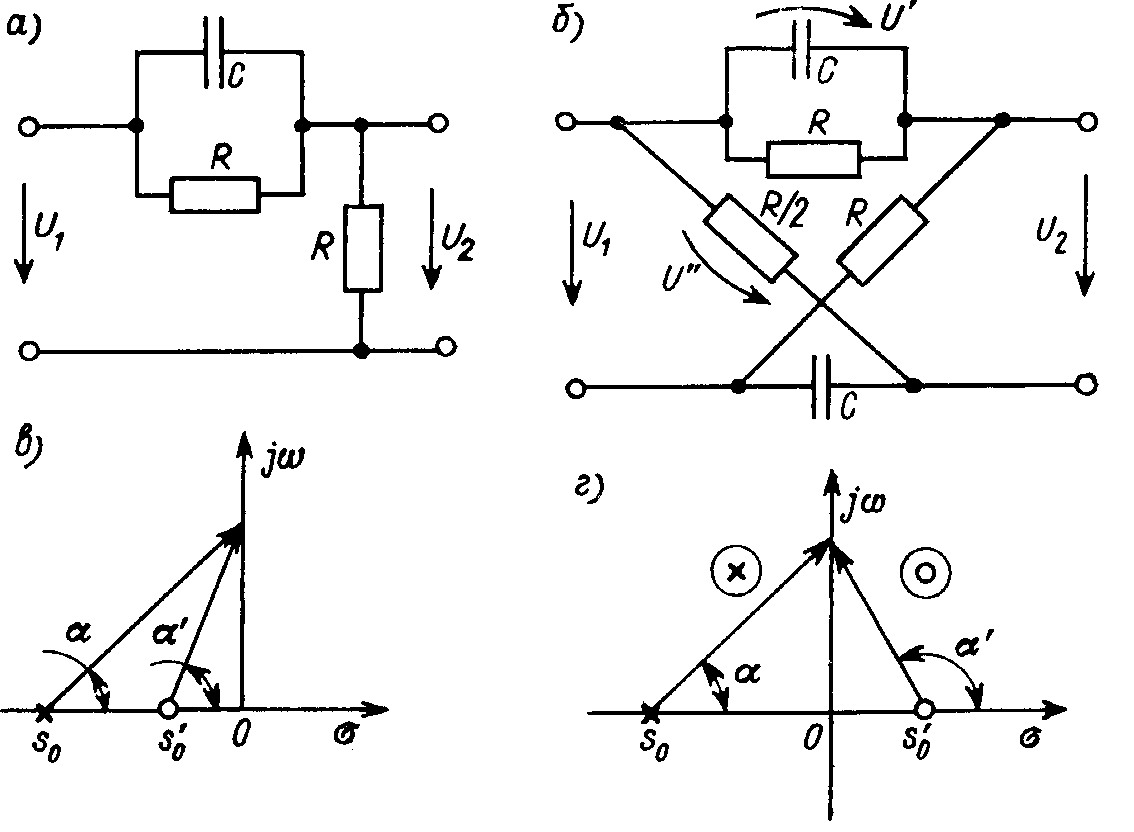
Первый представляет собой делитель напряжения, в плечах которого включены сопротивления 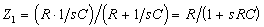и Z₂ = R. Поэтому его передаточная функция равна

.

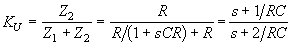Передаточную функцию по напряжению второго четырехполюсника найдем как разность падений напряжения на плечах моста, каждая из параллельных ветвей которого также является делителем напряжения U₁:

.

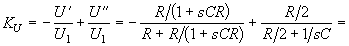
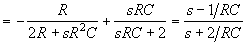Сопоставляя характер расположения полюсов и нулей двух цепей (рис. 22.4, в,г), приходим к выводу, что при одинаковых амплитудно-частотных характеристиках они обладают различными фазочастотными характеристиками.

11. Анализ устойчивости ТС: определения, критерии устойчивости, примеры анализа.

Под устойчивостью системы понимается способность ее возвращаться к состоянию установившегося равновесия после снятия возмущения, нарушившего это равновесие. Неустойчивая система непрерывно удаляется от равновесного состояния или совершает вокруг него колебания с возрастающей амплитудой.

Теорема Ляпунова – для того, чтобы система была устойчивой, нужно и достаточно, чтобы корни характеристик полинома системы (полюса) должны иметь отрицательные действительные части.

Критерий устойчивости Михайлова предназначен для оценки устойчивости системы по его характеристическому уравнению.

Порядок расчета устойчивости по критерию Михайлова:

Записывается характеристическое уравнение замкнутой системы:

.

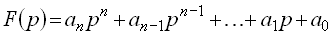Производится замена 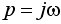и выделяются вещественная 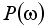и мнимая 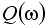слагаемые.

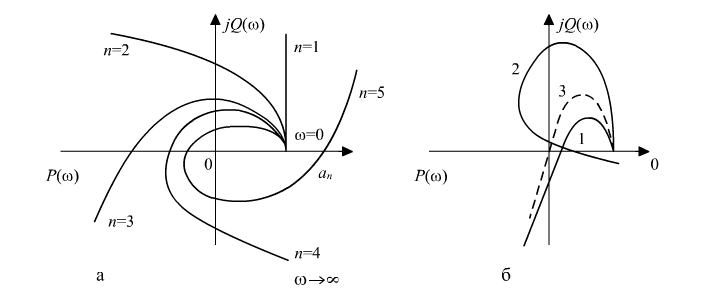Рис. 5.3. Годографы Михайлова для систем: а - устойчивых, б - неустойчивых

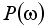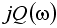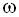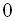В осях координат , при изменении от до 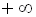строят характеристический частотный вектор (годограф Михайлова).

По виду годографа Михайлова судят об устойчивости системы. Устойчивые годографы проходят поочередно 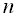квадрантов. На границе устойчивости системы годограф проходит через начало координат.

Системе, находящейся на границе устойчивости, соответствует годограф, проходящий через начало координат комплексной плоскости (кривая 3).

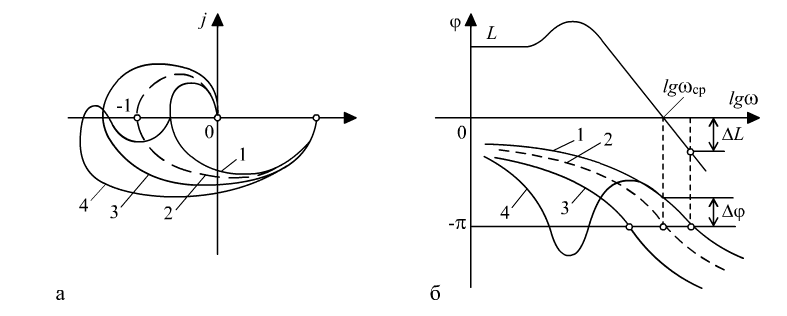
Критерий устойчивости Найквиста – позволяет судить об устойчивости замкнутой системы, если имеется информация об устойчивости разомкнутой системы.

Разомкнутая система устойчивая – надо, чтобы годограф не охватывал (-1;0)

Разомкнутая система неустойчивая – надо, чтобы годограф охватывал область (-1;0), число пересечений годографа отриц. действит. полуоси. Сверху вниз должно быть на k/2 больше направлений, где k-число полюсов передаточной ф-ии разомкнутой системы.