Классификация по способу представления объекта

Наряду с формальной классификацией, модели различаются по способу представления объекта:

§ Структурные или функциональные модели

Структурные модели представляют объект как систему со своим устройством и механизмом функционирования. Функциональные модели не используют таких представлений и отражают только внешне воспринимаемое поведение (функционирование) объекта. В их предельном выражении они называются также моделями «чёрного ящика». Возможны также комбинированные типы моделей, которые иногда называют моделями «серого ящика».

6. Операторные модели систем (частотные, преобразование Лапласа, Z-преобразование).

Операторные модели систем (частотные, преобразование Лапласа, Z-преобразование).
Преобразова́ние Лапла́са — интегральное преобразование, связывающее функцию 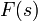комплексного переменного (изображение) с функцией 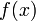вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.

Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так, свёртка двух функций сводится в пространстве изображений к операции умножения, а линейные дифференциальные уравнения становятся алгебраическими.

Z-преобразованием (преобразованием Лорана) называют свёртывание исходного сигнала, заданного последовательностью вещественных чисел во временно́й области, в аналитическую функцию комплексной частоты. Если сигнал представляет импульсную характеристику линейной системы, то коэффициенты Z-преобразования показывают отклик системы на комплексные экспоненты 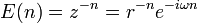, то есть на гармонические осцилляции с различными частотами и скоростями нарастания/затухания.

7. Свойства преобразования Лапласа.

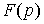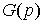В приводимых ниже формулах и являются преобразованиями Лапласа от функци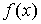й и 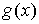соответственно.

1. Линейность. .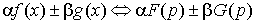

2. Теорема подобия. .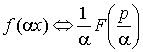

3. Дифференцирование оригинала. .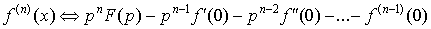

Именно это свойство и обеспечило такую популярность преобразованию Лапласа: оно операцию дифференцированияоригинала 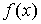заменяет операцией умноженияизображения на p. Это, конечно, сильно упрощает решение задач, где есть производные.

4. Дифференцирование изображения. .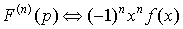

5. Интегрирование оригинала. .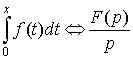

Наряду со свойством 3, это свойство является основным для приложений преобразования Лапласа, так как оно заменяет сложную операциюинтегрирования оригинала операцией деления изображения на p.
6. Интегрирование изображения. .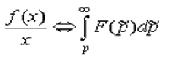

7. Теорема запаздывания. .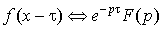

8. Теорема смещения. .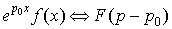

9. Теорема умножения. .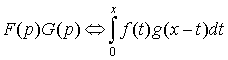

Комбинация 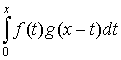называется сверткойфункци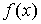й и 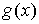и обозначают

символом 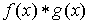. Эта операция также встречается очень часто при решении прикладных задач, и преобразование Лапласа позволяет заменить операцию свертки двух оригиналов операцией умножения их изображений.