Решение задачи об оптимальной диете: симплекс-метод в случае задачи на минимум

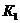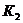Решение задач линейного программирования, связанных с минимизацией целевой функции, имеет некоторые особенности, которые мы рассмотрим здесь на примере задачи об оптимальной диете. Пусть в некоторой упрощённой ситуации фермеру-животноводу необходимо спланировать закупку кормов, и при этом на рынке имеется два вида подходящих ему кормов и по цене соответственно 3 и 4 денежные единицы за единицу веса. Фермер проконсультировался со специалистом по питанию животных и получил следующие рекомендации: в сутки каждое животное должно получать не менее 5 единиц углеводов, 3 единиц белков и 4 единиц витаминов (в некоторых соответствующих единицах). После этого фермер изучил состав питательных веществ кормов 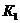и 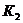, и выписал результат в виде таблицы (в тех же единицах):

Кол-во в одной единице веса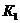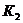
Углеводы
Белки
Витамины

Перед фермером возникла задача: в каком объёме закупать корма 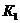и 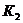, чтобы реализовать рекомендации специалиста и при этом потратить минимум денег?

Экономическое описание задачи у нас имеется, составим математическую модель. Обозначим ( , ) – объёмы закупок кормов 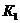и 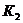в сутки на каждое животное. Аналогично предыдущему разделу мы получаем задачу линейного программирования: найти пару чисел ( , ), удовлетворяющую ограничениям

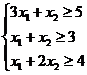(5.1)

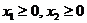
и минимизирующую целевую функцию

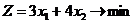. (5.2)

В этой задаче – только две неизвестные, поэтому имеется графический способ решения. Он проводится по схеме, объяснённой выше, и разобран здесь не будет.

Решение симплекс-методом осуществляется примерно так же, как и в предыдущем примере, поэтому разъясняться будут только его особенности для данного примера.

Итак, вначале мы заменяем все неравенства равенствами (теперь нам надо вычитать переменные, т.к. знак неравенств – другой):

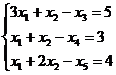(5.3)

, ,

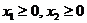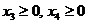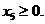
Тем самым, от задачи (5.1)-(5.2) мы переходим к равносильной ей задаче (5.3)-(5.2).

Начинаем аналогичные шаги нашей игры. Выражение базисных переменных 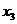, , 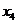первого шага через свободные , будет следующим:

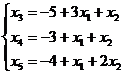(5.4)

Значит, базисное решение на первом шаге имеет вид (0, 0, -5, -3, -4) и не является допустимым!Не имеет никакого смысла вычислять значение целевой функции на нём и рассуждать, можно ли его улучшить (как мы это делали раньше). Для начала нам нужно добиться, чтобы базисное решение стало допустимым, т.е. чтобы все его компоненты стали неотрицательными. Из рассмотрения правых частей (5.4) ясно, что для этого можно увеличивать или (или оба одновременно, но мы опять будем изменять лишь одну переменную). В данном случае имеет смысл увеличивать , т.к. коэффициент при в целевой функции (5.2) меньше (не будем забывать, что в нынешнем примере мы минимизируем целевую функцию). Итак, пусть 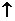и 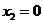. Тогда условия допустимости примут вид 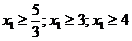. Естественно, мы возьмём самое наименьшее из возможных значений = 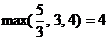. Далее становится новой базисной переменной, а на замену ей выходит переменная (значение 4 возникло из уравнения для в (5.4)). Итак, базисные переменные второго шага – , , 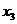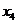; а свободные переменные – , . Выражаем базисные переменные через свободные (сначала − из последнего равенства в (5.4), а затем подставляем в остальные равенства этой системы):

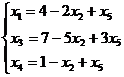(5.5)

И вот уже базисное решение второго шага получается допустимым – (4, 0, 7, 1, 0), и мы можем изучать его на оптимальность. Для этого выразим целевую функцию через свободные переменные второго шага (подставив в (5.2) выражение для из первого уравнения системы (5.5)):

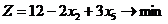
Видно, что мы ещё не достигли оптимума: в выражении для целевой функции имеется отрицательный коэффициент при одной из свободных переменных, увеличивая которую, мы сможем ещё уменьшить целевую функцию. Ясно, что в случае рассматриваемых задач на минимум условие завершения работы симплекс-метода состоит в том, что в выражении для целевой функции через свободные переменные все коэффициенты неотрицательны.Если это так, тосоответствующее базисное решение – оптимально.

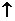У нас сейчас имеется коэффициент (-2) при , поэтому положим и =0. Аналогично изложенному выше, мы, с одной стороны, стремимся как можно сильнее увеличить (тем самым, как можно сильнее уменьшить Z ), но, с другой, нас ограничивают условия допустимости 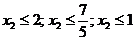. Значит, берём .

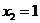Опуская детали, укажем, что на следующем шаге имеем следующее выражение базисных переменных этого шага , , 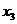через свободные переменные , :

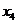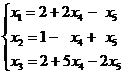
При этом выражение для целевой функции будет таким: 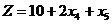. Теперь очевидно, что базисное решение (2, 1, 2, 0, 0) даёт самое наименьшее возможное значение целевой функции 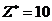. (В самом деле, для данного базисного решения 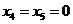и любое его изменение означает изменение 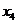, в сторону увеличения (т.к. они неотрицательны!) и увеличение целевой функции 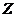.) Окончательно, в исходной формулировке решение даёт пара чисел 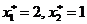; таким образом, нашему фермеру целесообразно закупать ежесуточно для каждого животного две единицы веса корма 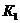и одну единицу веса корма 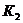. Задача решена.

Раздел 6

Двойственная задача линейного программирования на примере задачи торга

Вернёмся к экономическому примеру раздела 2 − заводу, выпускающему два вида продукции. Мы рассматривали задачу линейного программирования, связанную с выбором оптимального плана. Сейчас мы определим некоторую связанную с ней задачу, которую назовём двойственной по отношению к исходной.

Представим себе, что на календаре – 90-е годы, экономический кризис; и представим некоторую фирму, оптом скупающую у предприятий сырье с целью выгодной перепродажи за границу. И вот её представители начинают переговоры с рассматриваемым нами заводом. Их цель: скупить (по возможности дёшево) всё наше сырьё. Мы также отстаиваем свою выгоду. Начинается торг. Пусть 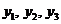− обсуждаемые цены за единицу сырья 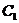, , 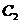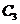. Пусть на наших складах хранится запас сырья на месяц, и переговоры ведутся именно об этих объёмах. Тогда, с учётом запаса сырья в расчёте на одни сутки, мы получаем, что цель фирмы-перекупщика в ходе торга – это

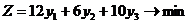(6.1)

(т.е. минимизация цены суточного запаса трёх видов сырья). Наш завод имеет дело со следующей альтернативой: либо использовать сырьё для производства и получить прибыль с конечной продукции, либо продать всё сырье перекупщику. Разумеется, мы выберем второй вариант только в том случае, если он будет нам более выгоден. Запишем это требование математически. Для этого обратимся к матрице технологических коэффициентов:

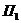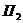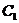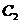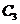Отсюда видно, что если мы используем 1 ед. сырья 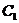, 1 ед. сырья 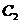и 2 ед. сырья 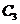в производстве (одной единицы продукции 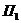, разумеется), то получим прибыль в 2 денежные единицы (по условию). Значит, перекупщик должен предложить нам не меньше за всё это сырьё, т.е. мы потребуем, чтобы выполнялось неравенство 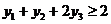. Аналогично, рассматривая выгодность сделки по отношению к второму виду продукции, получаем неравенство 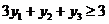. (Очевидно, что равенства нас устраивают, т.к. мы получаем ту же самую прибыль безо всяких усилий!). Итак, в совокупности наши условия на переговорах имеют вид:

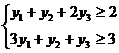(6.2)

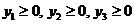
Задача линейного программирования (6.1)-(6.2) называется, по определению, двойственной по отношению к исходной задаче (2.1)-(2.2) из раздела 2.

Правило построения двойственной задачи может быть усмотрено из следующей таблицы:

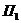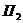		запасы
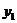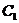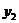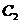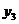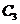	Прибыль

(6.3)

Сравнивая данную таблицу с формулировками задач (2.1)-(2.2) и (6.1)-(6.2), мы видим, что в исходной задаче ограничения и целевая функция записываются «по строкам», а в двойственной – «по столбцам». При этом в исходной задаче все ограничения – неравенства « 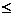» и целевая функция максимизируется, а в двойственной задаче все ограничения – « 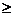» и целевая функция минимизируется. Ясно, что исходная задача однозначно восстанавливается по двойственной. Таким образом, имеются естественные пары взаимно-двойственных задач.

Раздел 7