Графический метод решения в случае двух переменных
В случае, когда в задаче линейного программирования искомых неизвестных величин только две (как в рассмотренном выше примере), возможно элементарное графическое решение. В самом деле, множество пар вещественных чисел (  ,
,  ) можно отождествить с множеством точек плоскости (посредством введения декартовой прямоугольной системы координат). Множество планов производства будет изображаться точками первой координатной четверти. План производства, удовлетворяющий всем ограничениям, называется допустимым планом. Выясним, какую фигуру образуют все допустимые планы задачи (2.1)-(2.2). Как известно из школьной математики, множество решений линейного неравенства с двумя переменными есть полуплоскость. Например, множество решений неравенства
) можно отождествить с множеством точек плоскости (посредством введения декартовой прямоугольной системы координат). Множество планов производства будет изображаться точками первой координатной четверти. План производства, удовлетворяющий всем ограничениям, называется допустимым планом. Выясним, какую фигуру образуют все допустимые планы задачи (2.1)-(2.2). Как известно из школьной математики, множество решений линейного неравенства с двумя переменными есть полуплоскость. Например, множество решений неравенства  есть замкнутая полуплоскость с границей (прямой линией)
есть замкнутая полуплоскость с границей (прямой линией)  . Нарисовать эту границу легче всего построив точки пересечения данной прямой с осями координат: (12,0) и (0,4). (В уравнении берём сначала
. Нарисовать эту границу легче всего построив точки пересечения данной прямой с осями координат: (12,0) и (0,4). (В уравнении берём сначала 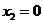 , затем
, затем  .) Затем через две эти точки проводим прямую. Получаем прямую DC на рис. 1. А вот выбрать, какая же из двух образующихся полуплоскостей будет искомой можно, заметив, что при фиксированном
.) Затем через две эти точки проводим прямую. Получаем прямую DC на рис. 1. А вот выбрать, какая же из двух образующихся полуплоскостей будет искомой можно, заметив, что при фиксированном  неравенство ограничивает
неравенство ограничивает  сверху: тем самым, искомая полуплоскость лежит снизу от прямой. Проделаем то же самое и с двумя другими неравенствами системы. (Числа 1, 2 и 3 на рисунке обозначают номер соответствующего неравенства в системе (2.2).) Пересечение трёх получающихся полуплоскостей с первой четвертью и будет искомым множеством допустимых планов – в нашем случае выпуклым пятиугольником OABCD:
сверху: тем самым, искомая полуплоскость лежит снизу от прямой. Проделаем то же самое и с двумя другими неравенствами системы. (Числа 1, 2 и 3 на рисунке обозначают номер соответствующего неравенства в системе (2.2).) Пересечение трёх получающихся полуплоскостей с первой четвертью и будет искомым множеством допустимых планов – в нашем случае выпуклым пятиугольником OABCD:

(Рис. 1)
Как теперь определить ту точку пятиугольника, для которой значение целевой функции будет максимальным? Для этого рассматривают так называемые линии уровня целевой функции – семейство параллельных прямых  . Вдоль каждой из этих прямых значение целевой функции одно и то же. Три из них обозначены на рисунке пунктирными линиями, а стрелкой обозначено направление роста целевой функции. (С линиями уровня вы уже, на самом деле, знакомы – вспомните линии постоянного давления на картах погоды, или линии постоянной высоты на картах местности.) Будем двигать линию уровня параллельно себе, как на рисунке, приближая её к многоугольнику допустимых планов (подобно чертёжной рейсшине). При этом значение целевой функции будет уменьшаться, и первая точка касания линии уровня с множеством допустимых планов (точка C на рисунке) и будет, очевидно, искомым оптимальным планом. Итак, в нашем случае это будет точка С(3,3) со значением целевой функции
. Вдоль каждой из этих прямых значение целевой функции одно и то же. Три из них обозначены на рисунке пунктирными линиями, а стрелкой обозначено направление роста целевой функции. (С линиями уровня вы уже, на самом деле, знакомы – вспомните линии постоянного давления на картах погоды, или линии постоянной высоты на картах местности.) Будем двигать линию уровня параллельно себе, как на рисунке, приближая её к многоугольнику допустимых планов (подобно чертёжной рейсшине). При этом значение целевой функции будет уменьшаться, и первая точка касания линии уровня с множеством допустимых планов (точка C на рисунке) и будет, очевидно, искомым оптимальным планом. Итак, в нашем случае это будет точка С(3,3) со значением целевой функции  . Таким образом, максимально возможную для завода ежесуточную прибыль 15 денежных единиц мы будем получать, если организуем ежесуточное производство трёх единиц продукции каждого вида.
. Таким образом, максимально возможную для завода ежесуточную прибыль 15 денежных единиц мы будем получать, если организуем ежесуточное производство трёх единиц продукции каждого вида.
Раздел 4
Симплекс-метод
Опишем теперь аналитический симплекс-метод решения задач линейного программирования, который в отличие от рассмотренного выше графического метода применим к задачам с любым числом неизвестных.
Первым этапом этого метода является переход от исходной задачи к эквивалентной ей задаче линейного программирования, в которой все ограничения имеют вид равенств. Идея здесь замечательна в своей простоте: каждое неравенство-ограничение мы заменяем равенством-ограничением, вводя дополнительную переменную с неотрицательными значениями (собственно, как и все остальные переменные в нашей задачи). Например, очевидно, что числа  и
и  удовлетворяют неравенству
удовлетворяют неравенству  тогда и только тогда, когда для некоторого неотрицательного числа
тогда и только тогда, когда для некоторого неотрицательного числа 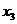 выполняется равенство:
выполняется равенство:  . Вводя аналогично переменные
. Вводя аналогично переменные 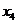 и
и  , перепишем систему (2.2) эквивалентно следующим образом:
, перепишем систему (2.2) эквивалентно следующим образом:
 (4.0)
(4.0)
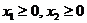 ,
, 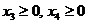 ,
, 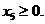
Нашу целевую функцию (2.1) мы можем теперь рассматривать и как функцию пяти переменных (  ,
,  , ..,
, ..,  ) (при этом она не зависит от последних трёх переменных). Ясно, что задачи (2.1)-(2.2) и (2.1)-(4.0) эквивалентны, и что оптимальное решение первой из них получается в виде первых двух компонент оптимального решения второй.
) (при этом она не зависит от последних трёх переменных). Ясно, что задачи (2.1)-(2.2) и (2.1)-(4.0) эквивалентны, и что оптимальное решение первой из них получается в виде первых двух компонент оптимального решения второй.
Итак, на втором этапе симплекс-метода мы будем решать задачу (2.1)-(4.0). Перепишем систему (4.0), выразив три «новые» переменные через первоначальные:
 (4.1)
(4.1)
В подобных случаях симплекс-метод использует следующие термины: переменные (их количество совпадает с числом уравнений), которые нам удалось выразить через остальные, называются базисными; а переменные, фигурирующие в правых частях систем вида (4.1) (т.е. через которые мы выразили базисные) носят название свободных. Смысл последнего термина ясен: эти переменные могут меняться почти что произвольно – будучи ограниченными лишь условиями неотрицательности всех переменных; при этом базисные переменные «следуют» за ними. В нашем конкретном случае системы (4.1) переменные 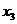 ,
, 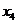 ,
,  являются базисными переменными; а
являются базисными переменными; а  ,
,  − свободными. Дальнейший ход симплекс-метода напоминает некоторую интересную игру, и я позволю себе привлечь некоторые … хоккейные аналогии. Итак, пять наших переменных
− свободными. Дальнейший ход симплекс-метода напоминает некоторую интересную игру, и я позволю себе привлечь некоторые … хоккейные аналогии. Итак, пять наших переменных  ,
,  , ..,
, ..,  мы уподобим хоккеистам, свободные из которых играют на площадке, а базисные наблюдают за игрой на скамейке запасных и готовы сменить кого-то из свободных. Пятиугольник допустимых планов (см. рис. 1) будет «площадкой» для пары (
мы уподобим хоккеистам, свободные из которых играют на площадке, а базисные наблюдают за игрой на скамейке запасных и готовы сменить кого-то из свободных. Пятиугольник допустимых планов (см. рис. 1) будет «площадкой» для пары (  ,
,  ) (разумеется, наша аналогия с хоккеем не будет полной). Таким образом, пара (
) (разумеется, наша аналогия с хоккеем не будет полной). Таким образом, пара (  ,
,  ) свободно двигается в рамках площадки, а движение остальных игроков (точнее, их голов и взглядов) следует за ними в соответствии с равенствами (4.1)! В чём же цель этих движений свободных игроков; иными словами, где расположены ворота (по-английски, «ворота» и «цель» выражаются словом goal, отсюда вратарь-голкипер − goalkeeper)? Цель, разумеется, состоит в максимизации целевой функции F ; стало быть, ворота − это искомый оптимальный план производства, отмеченный на рис. 1 точкой C!
) свободно двигается в рамках площадки, а движение остальных игроков (точнее, их голов и взглядов) следует за ними в соответствии с равенствами (4.1)! В чём же цель этих движений свободных игроков; иными словами, где расположены ворота (по-английски, «ворота» и «цель» выражаются словом goal, отсюда вратарь-голкипер − goalkeeper)? Цель, разумеется, состоит в максимизации целевой функции F ; стало быть, ворота − это искомый оптимальный план производства, отмеченный на рис. 1 точкой C!
Будем двигаться дальше. Как и в хоккее, в симплекс-методе можно будет заменять полевых игроков запасными до тех пор, пока ворота не будут взяты. При этом количество полевых игроков должно оставаться постоянным (в нашем примере, два). Каждый раз будет вычисляться так называемое базисноерешение: такой вектор (  ,
,  , ..,
, ..,  ), удовлетворяющий (4.0), у которого значения всех свободных переменных нулевые. Выскажем сразу следующее утверждение:
), удовлетворяющий (4.0), у которого значения всех свободных переменных нулевые. Выскажем сразу следующее утверждение:
Утверждение. Можно доказать, что среди всевозможных базисных решений задачи (2.1)-(4.0) всегда имеется оптимальное решение этой задачи. Таким образом, оптимальные решения достаточно разыскивать лишь среди базисных решений.
Итак, начинаем игру.
1-й шаг.
Будем фиксировать размещение игроков и базисное решение в следующей таблице:
| Шаг метода | Базисные | Свободные | Базисное решение |
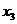 , , 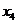 , ,  |  , ,  | (0, 0, 12, 6, 10) |
На каждом шаге нам необходимо будет выражение целевой функции через свободные переменные. В данный момент мы имеем выражение (2.1) и значение целевой функции на первом базисном решении равно нулю. Разумеется, из (2.1) видно, что его можно увеличить, увеличивая любую из свободных переменных  ,
,  . Здесь и в дальнейшем мы будем в такой ситуации изменять только одну из свободных переменных. Как правило, имеет смысл изменять переменную с наибольшим по модулю коэффициентом в выражении для целевой функции: в данный момент, переменную
. Здесь и в дальнейшем мы будем в такой ситуации изменять только одну из свободных переменных. Как правило, имеет смысл изменять переменную с наибольшим по модулю коэффициентом в выражении для целевой функции: в данный момент, переменную  . Обозначим этот процесс символически
. Обозначим этот процесс символически  (при этом
(при этом  остаётся нулём). Из выражения (2.1) видно, что нам хотелось бы сделать
остаётся нулём). Из выражения (2.1) видно, что нам хотелось бы сделать  как можно больше; но каковы пределы роста
как можно больше; но каковы пределы роста  ? Они определяются требованиями неотрицательности переменных в левых частях (4.1):
? Они определяются требованиями неотрицательности переменных в левых частях (4.1): 





Отсюда находим, что самое большое возможное значение  равно
равно 
Итак, мы положим  =4 и «отяжелевший» игрок
=4 и «отяжелевший» игрок  отправляется на скамейку запасных – становится базисной переменной. Выделим в (4.1) то уравнение, которое «породило» ограничение с четвёркой (единственное или, в общем случае, одно из нескольких):
отправляется на скамейку запасных – становится базисной переменной. Выделим в (4.1) то уравнение, которое «породило» ограничение с четвёркой (единственное или, в общем случае, одно из нескольких):

Тогда алгоритм симплекс-метода именно базисной переменной 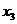 предписывает выйти на замену
предписывает выйти на замену  , т.е. стать свободной переменной. Итак, на втором шаге игры свободные переменные
, т.е. стать свободной переменной. Итак, на втором шаге игры свободные переменные  ,
, 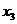 , а базисные
, а базисные  ,
, 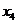 ,
,  . Теперь нам надо получить аналог системы (4.1) на втором шаге, т.е. выразить новые базисные переменные через новые свободные. Начинаем мы всегда с подчёркнутого уравнения, из которого выражаем
. Теперь нам надо получить аналог системы (4.1) на втором шаге, т.е. выразить новые базисные переменные через новые свободные. Начинаем мы всегда с подчёркнутого уравнения, из которого выражаем  Далее подставляем это выражение в правые части оставшихся уравнений системы (4.1) и получаем искомую систему
Далее подставляем это выражение в правые части оставшихся уравнений системы (4.1) и получаем искомую систему
 (4.2)
(4.2)
Замечание. Симплекс-метод обычно состоит из серии таких шагов, и вычислительные ошибки сводят на нет всю дальнейшую работу. Поэтому я рекомендовал бы вести записи вычислений предельно аккуратно: выписывать базисные и свободные переменные в порядке роста индексов; в системах вида (4.1), (4.2) записывать сначала числа одно под другим, потом свободные переменные в указанном порядке одно под другим.
В частности, при такой записи мы сразу видим в столбце чисел новое базисное решение: (0, 4, 0, 2, 6). Запишем его в обновлённую таблицу.
2-й шаг.
| Шаг метода | Базисные | Свободные | Базисное решение |
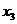 , , 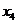 , ,  |  , ,  | (0, 0, 12, 6, 10) | |
 , , 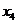 , ,  |  , , 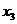 | (0, 4, 0, 2, 6) |
Запишем, наконец, выражение целевой функции через новые свободные переменные (подставив в (2.1) выражение для  из (4.2)):
из (4.2)):  .
.
Вспомним, что свободные переменные принимают лишь неотрицательные значения, и что мы стремимся к максимизации F. Для второго базисного решения  ; стало быть, для него значение целевой функции равно 12. Но ясно, что поскольку коэффициент при
; стало быть, для него значение целевой функции равно 12. Но ясно, что поскольку коэффициент при  положителен, мы можем добиться большего, увеличивая
положителен, мы можем добиться большего, увеличивая  . Итак, пусть
. Итак, пусть  а
а  .
.
Аналогично вышеизложенному, положим  Тем самым, переменная
Тем самым, переменная  становится базисной (переходит на скамейку запасных), а переменная
становится базисной (переходит на скамейку запасных), а переменная 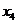 − свободной. (Поскольку именно выражение для
− свободной. (Поскольку именно выражение для 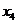 в (4.2) «породило» ограничение с тройкой.) Далее, как и ранее, из этого выражения находим
в (4.2) «породило» ограничение с тройкой.) Далее, как и ранее, из этого выражения находим  И, наконец, подставляя последнее выражение в остальные уравнения (4.2), получим систему
И, наконец, подставляя последнее выражение в остальные уравнения (4.2), получим систему
 (4.3)
(4.3)
Видно, что очередным базисным решением будет вектор (3, 3, 0, 0, 1) и, стало быть, можно продолжить нашу таблицу.
3-й шаг.
| Шаг метода | Базисные | свободные | Базисное решение |
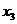 , , 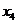 , ,  |  , ,  | (0, 0, 12, 6, 10) | |
 , , 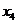 , ,  |  , , 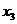 | (0, 4, 0, 2, 6) | |
 , ,  , ,  | 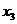 , , 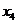 | (3, 3, 0, 0, 1) |
Выражение для целевой функции через свободные переменные третьего шага будет следующим:  . Таким образом, значение F на третьем базисном решении равно 15 и, более того, лучшего нам не добиться: переменные
. Таким образом, значение F на третьем базисном решении равно 15 и, более того, лучшего нам не добиться: переменные 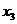 ,
, 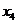 принимают лишь неотрицательные значения. Шайба в воротах и наша игра закончена!
принимают лишь неотрицательные значения. Шайба в воротах и наша игра закончена!
Итак, целевая функция принимает наибольшее возможное значение  при
при  . (Разумеется, наш ответ совпал с ответом, полученным графическим методом.)
. (Разумеется, наш ответ совпал с ответом, полученным графическим методом.)
Можно сформулировать в общем виде признак «взятия ворот», т.е. критерий оптимальности базисного решения, полученного на некотором шаге симплекс-метода:
Базисное решение задачи линейного программирования на максимум является оптимальным (т.е. даёт искомый максимум), если в выражении целевой функции через свободные переменные данного шага все коэффициенты неположительны (т.е. отрицательны или равны нулю).
Раздел 5
