Графический метод решения ЗЛП

Если задача линейного программирования в стандартной форме

содержит всего лишь две переменные x₁ и x₂ (т.е. n=2),

то ее можно решить следующим способом, основанным

на ее геометрической интерпретации.Каждое неравенство

системы ограничений и условие неотрицательности представляют

собой полуплоскость. Пересечение полуплоскостей образует

выпуклое многоугольное множество

(многогранник допустимых решений).

Целевая функция графически изображается

множеством параллельных прямых, называемых

линиями уровня, каждой из которых соответствует

конкретное значение z.Для решения задачи линия

уровня сдвигается в пределах области допустимых

решений (многогранника допустимых решений)

в направлении вектора-градиента

gradz = f¢(x) = 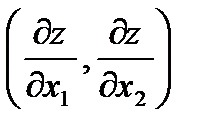до самой крайней

точки области для задачи максимизации, и

в направлении антиградиента– gradz= 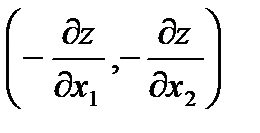для

задачи минимизации. Координаты этой точки и

определяют решение ЗЛП (оптимальный план задачи).

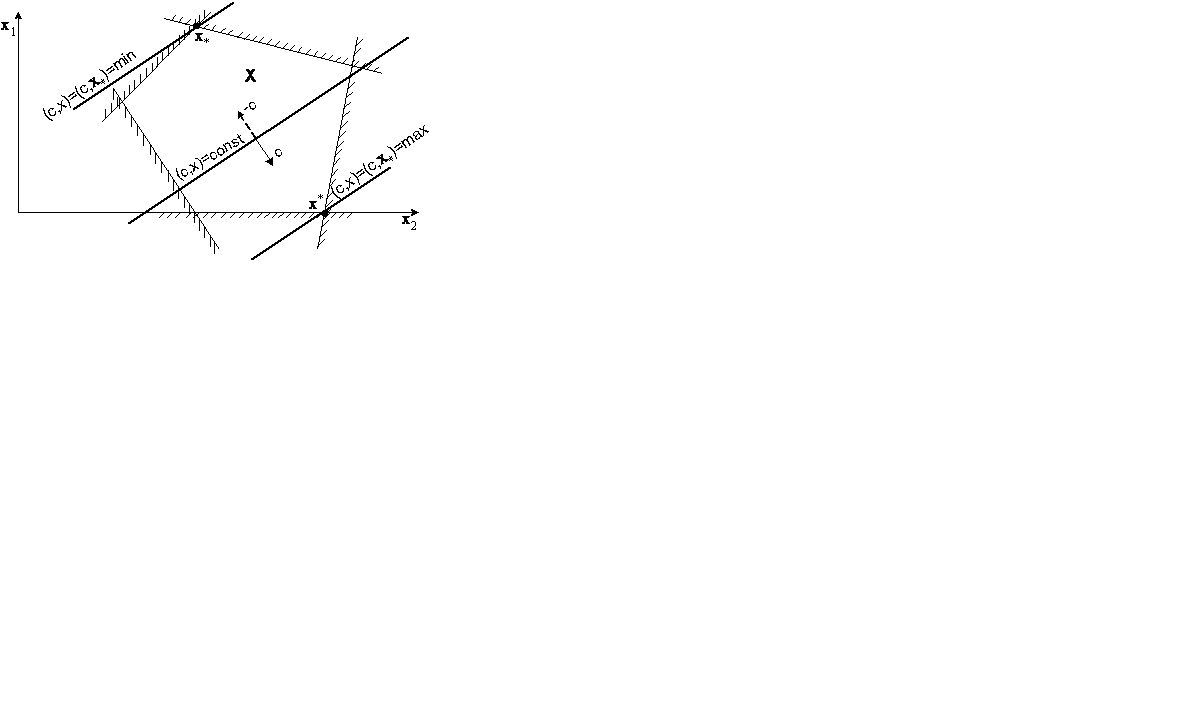
Рис1. Геометрическая интерпретация ЗЛП в стандартной форме

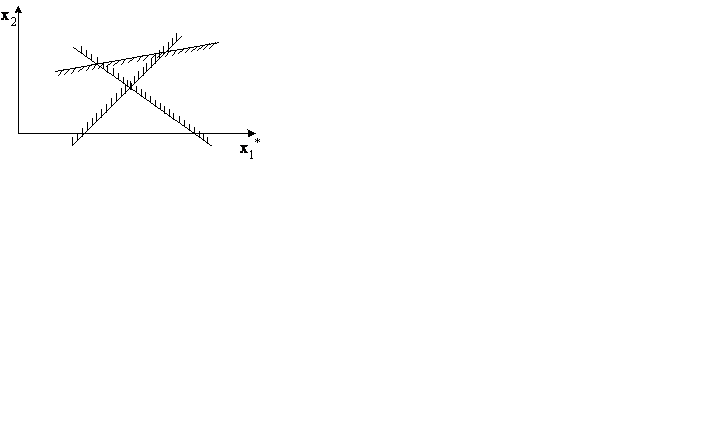
Рис.2 Пример пустой области допустимых решений (X)

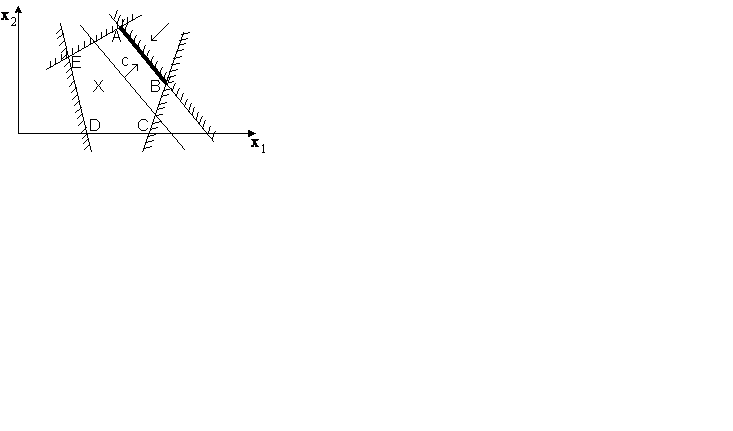
Рис.3 Пример ЗЛП, имеющий бесконечное множество решений (ребро АВ многогранника допустимых решений ABCDE)

48. симплекс-метод решения ЗЛП: идея метода и построение первоначального базисного плана. Симплексная таблица.

идея заключается в том, что, начиная с некоторого исходного невырожденного базисного плана , осуществляется последовательно направленное перемещение по опорным решениям задачи – вершинам ОДР к оптимальному плану. При этом значение целевой функции для задач на максимум не убывает. Через конечное число шагов получим оптимальное решение или установим неограниченность целевой функции на ОДР.

Допустим, имеется исходная ЗЛП в канонической форме:
F(X)=c₁X₁+c₂X₂+...+c_nX_n =>max

a_1,1X₁+a_1,2X₂+...+a_1,nX_n=b₁
a_2,1X₁+a_2,2X₂+...+a_2,nX_n=b₂
. . . . . . . . . . . . . . . . . . . . .
a_m,1X₁+a_m,2X₂+...+a_m,nX_n=b_m

В общем случае m любых переменных можно выразить через оставшиеся (n-m) переменных, например - X₁...X_m через X_m+1...X_n:

X₁=B₁-(A_1,m+1X_m+A_1,m+2X_m+2+...+A_1,nX_n)
...........................................................
X_m=B_m-(A_m,m+1X_m+1+A_m,m+2X_m+2+...+A_m,nX_n)

ЗдеськоэфициентыВ_i иА_i,j выражаютсячерезb_i иa_i,j.
Переменные X₁... X_m называются базисными, а X_m+1...X_n- свободными.
Если положить X_m+1=...=X_n=0, то X_i=B_i и если при этом все B_i =0, то и X_i =0, и такой вектор: X=(B₁, B₂, ..., B_m, 0, 0 ,..., 0) называется базисным Выражение целевой функции через свободные переменные:
F=C₀-(C_m+1X_m+1+...+ C_nX_n)
Здесь коэффициенты C₀, C_m+1, ..., C_n выражаются через с_j, B_i, a_{i, j}.

Начальная симплекс-таблица

Составим по этим данным так называемую начальную симплекс-таблицу.

Базис. Перем.	Своб. Перем.	X1	.......	Xi	.......	Xm	Xm+1	.......	Xk	.......	Xn
X1	B1		.......		.......		A1,m+1	.......	A1,k	.......	A1,n
X2	B2		.......		.......		A2,m+1	.......	A2,k	.......	A2,n
.....	.....	.....	.....	.....	.....	.....	.....	.....	.....	.....	.....
Xi	Bi		.......		.......		Ai,m+1	.......	Ai,k	.......	Ai,n
.....	.....	.....	.....	.....	.....	.....	.....	.....	.....	.....	.....
Xm	Bm		.......		.......		Am,m+1	.......	Am,k	.......	Am,n
F(X)	C0		.......		.......		Cm+1	.......	Ck	.......	Cn

Замечание: В простейшем случае в качестве базисных переменных можно взять такие m переменных, каждая из которых входит только в одно ограничение, причем с положительным знаком, а все свободные члены b_i>0.

48-1. симплекс-метод решения ЗЛП: проверка плана на оптимальность.

Критерием оптимальности рассматриваемого плана является выполнение условия

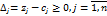
Возможны три случая:

1. Все оценки 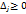тогда найденный базисный план оптимален.

2. Для некоторого j оценка 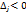и все элементы 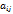соответствующего столбца 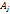неположительные,. В этом случае задача неразрешима, те целевая функция не ограничена на множестве допустимых планов(z стремится к бесконечности)

3. Среди оценок 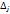есть отрицательные, причем для каждого номера j с 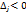в соответствующем столбце 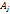имеются положительные элементы 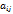. Тогда план не явл-ся оптимальным и следует искать новый базисный план, при котором значение целевой функции z было бы не меньше.

49.симплекс-метод решения ЗЛП: переход к новому плану.

1. Выбрать свободную переменную, которую надо ввести в базис (выбор разрешающего столбца): это столбец, с минимальным значением С_j (пусть это k-й столбец)

2. Выбрать базисную переменную, которую надо вывести из базиса (выбор разрешающей строки): рассмотрим k-й столбец и все его элементы, которые больше нуля, т.е. A_i,k>0; для всех этих элементов находим отношение B_i/A_i,k и выбираем строку, которая соответствует минимальному значению этого отношения (пусть это i-я строка); соответствующая i-я переменная X_i выводится из базиса; при нескольких одинаковых отношениях берем любую строку; элемент A_i,k называется разрешающим элементом.

3. Пересчитать симплекс-таблицу: составляем новую симплекс-таблицу заменив в составе базисных переменных X_i на X_k; заполняем сначала новую k-ю строку, записывая в нее элементы старой i-ой строки, поделенные на разрешающий элемент; после заполнения k-ой строки заполняем оставшиеся строки; для этого k-ю строку умножаем последовательно на такие числа, чтобы после сложения ее с каждой строкой старой таблицы в k-ом столбце получить везде ноль (кроме единицы в k-ой строке).