Суть и причины автокорреляции

Автокорреляция — корреляционная зависимость между текущими уровнями некоторой переменной и уровнями этой же переменной, сдвинутыми на несколько периодов времени назад

Автокорреляция случайной составляющей ε — корреляционная зависимость текущих 𝜀_𝑖 и предыдущих и 𝜀_𝑖−𝐿 значений случайной составляющей. Величина L называется запаздыванием, сдвигом во времени или лагом. Лаг определяет порядок автокорреляции. Автокорреляция случайной составляющей нарушает 3-ю предпосылку нормальной линейной модели регрессии: случайные отклонения 𝜀_𝑖 и 𝜀_𝑗 (i ≠ j) не коррелируют (отсутствует автокорреляция): 𝑀(𝜀_𝑖 , 𝜀_𝑗)= 0, 𝑖 ≠ 𝑗. Обычно автокорреляция встречается при использовании данных временных рядов. Допустим, что случайная составляющая обусловлена только невключением в модель объясняющих переменных. Тогда, если значение 𝜀_𝑖 в i-м наблюдении должно быть независимым от его значения в предыдущем (i - L)-oм наблюдении 𝜀_𝑖−𝐿 , то и значение любой факторной переменной, «скрытой» в ε, должно быть некоррелированным с ее значением в предыдущем наблюдении.

Причины: ошибки спецификации; инерция в изменении экономических показателей; эффект паутины; сглаживание данных.

Автокорреляция может быть как положительной, так и отрицательной. Положительная автокорреляция означает постоянное в одном направлении действие неучтенных факторов на результат. Отрицательная автокорреляция означает разнонаправленное действие неучтенных в модели факторов на результат, что приводит к отрицательной корреляции между последовательными значениями случайной составляющей. То есть за положительными значениями случайной составляющей 𝜀_𝑖 в одном наблюдении следуют отрицательные значения 𝜀_𝑗 и в следующем, и наоборот. Заметим, что отрицательная автокорреляция в экономике встречается относительно редко.

29. Последствия автокорреляции в определенной степени сходны с последствиями гетероскедастичности. Среди них при применении МНК выделяют следующие. 1. Оценки параметров, оставаясь несмещенными и линейными, перестают быть эффективными. Поэтому, они перестают обладать свойствами наилучших линейных несмещенных оценок. 2. Дисперсии оценок коэффициентов являются смещенными. Дисперсии часто, являются заниженными, что влечет за собой увеличение t-статистик. 3. Оценка дисперсии регрессии S² является смещенной оценкой истинного значения σ² , во многих случаях занижая его. 4. Выводы по t- и F-статистикам, определяющим значимость коэффициентов регрессии уравнения и коэффициента детерминации R² , возможно, будут неверными. Вследствие этого ухудшаются прогнозные качества модели.

30. Обнаружение автокорреляции случайной составляющей. Оценкой случайной составляющей является остаток — разность между фактическим и рассчитанным по оцененному уравнению регрессии значениями признака-результата. Так как автокорреляция случайных составляющих имеет место, в основном, когда исходные данные являются временными рядами, обозначим номер наблюдения как t: (t = 1,…,n). Тогда для t-го наблюдения остаток будет равен 𝑒_𝑡 = 𝑦_𝑡 − 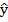_𝑡 . Возможные методы обнаружения автокорреляции остатков, (следовательно, и случайных составляющих): Метод рядов, Критерий Дарбина-Уотсона – наиболее известный критерий обнаружения автокорреляции. (существуют 4 ограничения использования данного метода)

Устранение автокорреляции

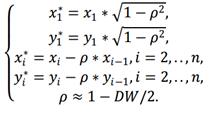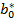Используем авторегрессонную схему первого порядка AR(1). Вместо переменных x, y рассмотрим новые переменные x*, y*, значения которых вычисляются по правилу: Пусть =b₀(1 − 𝜌). Коэффициент 𝜌 = 1 − 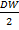= 0,4205. С помощью обычного МНК по переменным x* и y* оцениваем коэффициенты уравнения 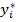= 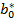+ 𝑏₁ 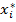. Далее находим 𝑏₀ = 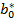/(1 − 𝜌).

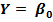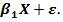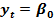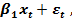
Так как автокорреляция чаще всего вызывается неправильной спецификацией модели, то необходимо, прежде всего, скорректировать саму модель. Для простоты изложения AR(1) рассмотрим модель парной линейной регрессии: + Тогда наблюдениям t и (t - 1) соответствуют формулы: + + 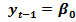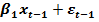Пусть случайные отклонения подвержены воздействию авторегрессии первого порядка: 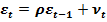, где — случайные отклонения, удовлетворяющие всем предпосылкам МНК, а коэффициент 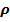известен. 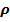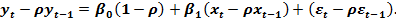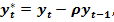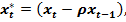Вычтем из второй формулы соотношение третьей, умноженное на : Положив 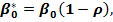получим: .

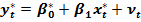Так как по предположению коэффициент 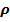известен, то очевидно, у*, x_t, v_t вычисляются достаточно просто. В силу того что случайные отклонения v_t удовлетворяют предпосылкам МНК, оценки параметров в 0 и в 1 будут обладать свойствами наилучших линейных несмещенных оценок.