Стандартная схема анализа функциональных зависимостей состоит в осуществлении ряда последовательных процедур.

· Подбор начальной модели. Он осуществляется на основе экономической теории, предыдущих знаний об объекте исследования, опыта исследователя и его интуиции.

· Оценка параметров модели на основе имеющихся статистических данных.

· Осуществление тестов проверки качества модели (обычно используются t-статистики для коэффициентов регрессии, F-статистика для коэффициента детерминации, статистика Дарвина-Уотсона для анализа отклонений и ряд других тестов).

· При наличии хотя бы одного неудовлетворительного ответа по какому-либо тесту модель совершенствуется с целью устранения выявленного недостатка.

· При положительных ответах по всем проведенным тестам модель считается качественной. Она используется для анализа и прогноза объясняемой переменной.

Несколько важных замечаний. 1. Необходимо предостеречь от абсолютизации полученного результата, поскольку даже качественная модель является подгонкой спецификации модели под имеющийся набор данных. Реальна картина, когда исследователи, обладающие разными наборами данных, строят разные модели для объяснения одной и той же переменной. 2. Проблематичным является и использование модели для прогнозирования значений объясняемой переменной. Иногда хорошие с точки зрения диагностических тестов модели обладают весьма низкими прогнозными качествами. 3. Одно из главных направлений эконометрического анализа — постоянное совершенствование моделей. Важно, какого-то глобального подхода, определяющего заранее возможные пути совершенствования модели, нет и быть не может. Нужно помнить, что совершенной модели не существует. В силу постоянно изменяющихся условий протекания экономических процессов не может быть и постоянно качественных моделей. Новые экономические условия требуют пересмотра даже весьма устойчивых моделей.4. Достаточно спорным является вопрос, как строить модели: а) начинать с самой простой и постоянно усложнять ее; б) начинать с максимально сложной модели и упрощать ее на основе проводимых исследований. Оба подхода имеют как достоинства, так и недостатки. Например, если следовать схеме а), то происходит обыкновенная подгонка модели под эмпирические данные. При теоретически более оправданном подходе б) поиск возможных направлений совершенствования модели зачастую сводится к полному перебору, что делает проводимый анализ неэффективным. На этапах упрощения модели возможно также отбрасыва-ние объясняющих переменных, которые были бы весьма полезны в упрощенной модели.

Вывод: построение модели является индивидуальным в каждой конкретной ситуации и опирается на серьезные знания экономической теории и статистического анализа.

Суть гетероскедастичности.

Гетероскедастичность - ситуация, когда дисперсия ошибки в уравнении регрессии изменяется от наблюдения к наблюдению. В этом случае приходится подвергать определенной модификации МНК (иначе возможны ошибочные выводы). Для обнаружения гетероскедастичности обычно используют 3 теста: тест ранговой корреляции Спирмена, тест Голдфеда-Квандта и тест Глейзера.

Гетероскедастичность может иметь место и при использовании в качестве данных наблюдений временных рядов (𝑥_𝑡 , 𝑦_𝑡). Если значения 𝑥_𝑡 и 𝑦_𝑡 увеличиваются со временем, то, возможно, и дисперсия случайной составляющей также будет расти со временем. Наличие гетероскедастичности можно проследить из графика зависимости квадрата остатков 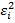от значения объясняющего признака 𝑥_𝑖. Если все отклонения находятся внутри полосы постоянной ширины, параллельной оси абсцисс, гетероскедастичность не наблюдается. Во всех остальных случаях гетероскедастичность наблюдается.

21. Последствия гетероскедастичности:

· Оценки коэффициентов по-прежнему останутся несмещёнными и линейными

· Оценки не будут эффективными (т. е, они не будут иметь наименьшую дисперсию по сравнению с другими оценками данного параметра), Они не будут даже асимптотически эффективными. Увеличение дисперсии оценок снижает вероятность получения максимально точных оценок

· Дисперсии оценок будут рассчитываться со смещением.

Поэтому выводы, получаемые на основе соответствующих t- и F- статистик, а также интервальные оценки коэффициентов регрессии будут ненадежными. Следовательно, статистические выводы, могут быть ошибочными и приводить к неверным заключениям по построенной модели.

Наличие гетероскедастичности случайных ошибок приводит к неэффективности оценок, полученных с помощью метода наименьших квадратов. Кроме того, в этом случае оказывается смещённой и несостоятельной классическая оценка ковариационной матрицы МНК- оценок параметров. Следовательно, статистические выводы о качестве полученных оценок могут быть неадекватными. В связи с этим тестирование моделей на гетероскедастичность является одной из необходимых процедур при построении регрессионных моделей.

22. Обнаружение гетероскедастичности в каждом конкретном случае является сложной задачей. Для знания дисперсий отклонений необходимо знать распределение случайной величины Y, соответствующее выбранному значению 𝑥_𝑖 . Практически, для каждого конкретного значения 𝑥_𝑖 определяется единственное значение 𝑦_𝑖 , что не позволяет оценить дисперсию случайной величины Y. Поэтому, не существует какого-либо однозначного метода определения гетероскедастичности.

Для определения наличия в выборке гетероскедастичностс используются тесты: графический анализ остатков, тест ранговой корреляции Спирмена, тест Глейзера и тест Голдфельда-Квандта. Выбор обусловлен относительной простотой тестов и наиболее частым их употреблением.

Тест Голдфелда Квандта. Тест выполняется в предположении, что стандартное отклонение 𝜎_𝑖 = 𝜎(𝜀)_𝑖 пропорционально значению переменной X в этом наблюдении, т.е. 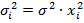, 𝑖 = 1,2, … ,𝑛. Второе предположение - 𝜀_𝑖 имеет нормальное распределение и отсутствует автокорреляция остатков. Последовательность теста Голдфелда-Квандта: 1. Все 𝑛 наблюдений удорядочиваются по величине X. 2. Вся упорядоченная выборка после этого разбивается на три группы (подвыборки) размерностей k, (𝑛 - 2k), k соответственно.3. Оцениваются отдельно регрессии для первой подвыборки (k первых наблюдений) и для третьей подвыборки (k последних наблюдений). Если предположение о пропорциональности дисперсий отклонений значениям X верно, то дисперсия регрессии по первой подвыборке (сумма квадратов отклонений) 𝑆₁ = 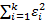будет существенно меньше дисперсии регрессии по третьей подвыборке (суммы квадратов отклонений) 𝑆₃ = 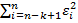. 4. Для сравнения дисперсий 𝑆₁ и 𝑆₃ строится следующая F-статистика: F= 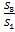∙ 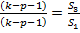, где p – число объясняющих переменных в каждом уравнении регрессии.

При сделанных предположениях относительно случайных отклонений, построенная 𝐹 -статистика имеет распределение Фишера с числами степеней свободы 𝜈₁ = 𝜈₂ = 𝑘 − 𝑝 − 1. 5. Если 𝐹набл = 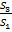> 𝐹кр = 𝐹_{𝛼;𝜈1;𝜈2} , то гипотеза об отсутствии гетероскедастичности отклоняется. Здесь 𝛼 — выбранный уровень значимости. Отметим, этот тест предназначен для анализа больших массивов данных и не всегда его результаты совпадают с результатами других тестов при недостаточном числе наблюдений.