Корреляционная зависимостьуровней ряда

Автокорреляцией уровней называется корреляционная зависимость между последовательными уровнями динамического ряда. Величины

называются коэффициентами автокорреляции уровней первого и второго порядков, соответственно. Обычно автокорреляцию изучают, начиная со сдвига на один шаг времени, затем на два и т.д. Практическими исследованиями установлено: максимальный порядок рассчитываемого коэффициента корреляции не должен быть больше , где n – число уровней исходного ряда.

Если временной ряд имеет только тенденцию и случайную компоненту, то максимальное или немного меньшее значение наблюдается у коэффициента автокорреляции первого порядка, так как тесно связанными оказываются каждые два соседних уровня. Если наблюдаются близкие к единице значения коэффициентов автокорреляции более высоких порядков, то это свидетельствует о наличии во временном ряде периодических колебаний, период которых равен порядку соответствующего коэффициента корреляции.

Лагом называется число шагов, по которым вычисляется коэффициент автокорреляции. В приведенных формулах, вычисляется с лагом или, по-другому, сдвигом в один шаг, а – в два шага. В буквальном смысле, в переводе с английского лаг – запаздывание.

Автокорреляционной функцией временного ряда называется последовательность коэффициентов автокорреляции первого, второго, третьего и последующих порядков.

Кореллограммой называется график зависимости значений автокорреляционной функции от величины лага (порядка коэффициента автокорреляции).

При наличии во временном ряде тенденции (тренда) и периодических изменений уровней ряда, между значениями уровней существует корреляция. Другими словами, периодическая зависимость формально может быть определена как корреляционная зависимость некоторого порядка L, где L– лаг. Так, период колебаний равен порядку L соответствующего коэффициента корреляции. Таким образом, сезонные компоненты могут быть найдены из автокореллограммы.

Пусть проведено аналитическое выравнивание уровней ряда и построена кривая устойчивой динамики экономического показателя – тренд. Теперь необходимо оценить качество построенной модели, т.е. проверить ее точность и адекватность реальному экономическому процессу. Точность модели оценивается близостью расчетных данных – фактическим. Проверка адекватности модели проводится на основе анализа свойств остатков При этом адекватность считается более важной характеристикой, чем точность.

Наиболее часто используемой характеристикой точности модели динамического ряда является дисперсия остатков или среднеквадратическая ошибка. В частности, для линейной модели тренда имеем

Если вычисляемая ошибка является несмещенной, т.е. 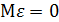, то Среднеквадратическая ошибка всегда несколько больше средней абсолютной ошибки имеющей похожий со среднеквадратической ошибкой смысл. Обе они характеризуют среднюю удаленность расчетных данных от фактических.Модель временного ряда считается точной, если не больше 5% среднего значения показателя .

Для оценки точности используется так же относительная ошибка аппроксимации

Модель считается точной, если

Оценка адекватности модели.

Проверка предпосылок МНК

Если уровни ряда выявлены верно, т.е. в соответствие с экономическим смыслом задачи, то остатки должны удовлетворять требованиям МНК. Оценка адекватности модели базируется на проверке выполнения предпосылок МНК (были сформулированы ранее).

1) Проверка выполнения условия 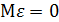проводится на основе нулевой гипотезы . Строится t-статистика

где – среднее арифметическое, . Гипотеза принимается, если – критерий Стьюдента с уровнем значимости α и количеством степеней свободы .

2) Проверка случайности ряда остатков может быть проведена разными способами.

2.1) Критерий серий. Расположим величины в порядке возрастания и найдем медиану , т.е. срединное значение при нечетном nи среднее арифметическое двух срединных значений –при четном n. Далее будем строить серии, т.е. последовательности из ряда остатков подряд расположенных членов, для которых имеют один и тот же знак. Если модель правильно отражает исследуемую зависимость, то она часто пересекает ломаную линию исходных данных и тогда серий много, а их длина невелика.

Сравнивая исходную последовательность с медианой, будем ставить знак +, если и знак –, если Если , то не учитывается. В результате получим последовательность плюсов и минусов, с общим числом, не превосходящим n членов ряда. Для того чтобы последовательность была случайной требуется, чтобы протяженность самой длинной серии была не слишком большой, а общее число серий наоборот – большим.

Пусть протяженность самой длинной серии а общее число серий . Последовательность остатков признается случайной, если:

а) – протяженность самой длинной серии;

б) , где – целая часть числа, – общее число серий. Если хотя бы одно из двух требований не выполняется, то гипотеза о случайности остатков отвергается и, следовательно, подтверждается наличие зависящей от времени неслучайной компоненты в разложении модели

Критерий поворотных точек.

Рассматриваем ряд остатков. Считаем точку поворотной точкой и присваиваем ей значение 1, если или . В противном случае точка не считается поворотной и ей присваивается значение 0.

Свойство случайности с уровнем значимости 0,05 выполняется, если фактическое количество поворотных точек больше расчетного (целого):

.

3) Отсутствие автокорреляции проверяется с помощью критерия Дарбина-Уотсона (Д-У). Рассчитывается величина

Допустим, что средний уровень остатков равен нулю, т.е. , тогда (первый коэффициент автокорреляции). Если допустить, что (чем больше объем выборки, тем точнее это соотношение), то

Отсюда видно, что если , т.е. автокорреляция остатков отсутствует, то .При полной автокорреляции равно 0, если или 4, если .

Обратимся к основной формуле. Если , то теоретически присутствует положительная автокорреляция, если , то имеет место отрицательная связь. В этом случае переходят к анализу величины и в дальнейшем используется . Расчетное значение критерия (или ) сравнивается с табличными: нижним и верхним критическими значениями статистики Д-У. Анализ наличия/отсутствия автокорреляции можно проводить и непосредственно.

Если окажется то принимается положительная автокорреляция, а модель признается неадекватной.

Если окажется то автокорреляция отвергается.

Если окажется или , то ничего определенного о автокорреляции остатков сказать нельзя и требуются дальнейшие исследования, например, вычисление коэффициента корреляции первого порядка, увеличение числа наблюдений, уточнение уравнения тренда и др.

Если окажется то принимается отрицательная автокорреляция, а модель признается неадекватной.

Пример. Пусть вычисленный коэффициент автокорреляции первого порядка есть . Для заданного количества параметров при факторных признаках и известном количестве наблюдений известны критические значения и , которые разбивают отрезок на пять частей. Вычислим величину . Проведем анализ.

На отрезке – положительная автокорреляция.

На отрезке – область неопределенности.

На отрезке – нет автокорреляции.

На отрезке – область неопределенности.

На отрезке – отрицательная автокорреляция.

Поскольку, в нашем случае , то можно сделать вывод о том, что автокорреляция отсутствует.

Если между уровнями ряда обнаружена автокорреляция, то каждый уровень можно рассматривать как функцию предыдущих значений уровней. Уравнение, определяющее такую зависимость, называется уравнением авторегрессии. Самый простой вид такой зависимости выражает линейная функция .

Отсутствие автокорреляции обеспечивает эффективность и состоятельность оценок коэффициентов модели.

4) Соответствие распределения остатков закону Гаусса проверяется с помощью R/S-критерия

Если расчетное значение R/S попадает между табулированными, то гипотеза о нормальном распределении остатков принимается. Для числа наблюдений

– для n =10 =>R/S = 2.67 … 3.685

– для n =20 =>R/S = 3,18 … 4,49

– для n =30 =>R/S = 3,47 … 4,89

при уровне значимости 0,05, то H₀ – гипотеза о ненормальном распределении отвергается и принимается H₁ – гипотеза о нормальном распределении .

Модель признается адекватной, если выполнены все требования, предъявляемые к остаткам. Описанная выше техника оценки параметров модели и уравнения в целом без изменений переносится и на временные ряды, в частности, если коэффициент детерминации существенно отличен от нуля, то это означает неравенство нулю коэффициентов регрессии и трендовую компоненту можно использовать для прогноза.