Принципы отбора факторов модели

Не включенные в модель и, соответственно, неучтенные в ней прочие факторы могут составить значительную долю в общей вариации результативного признака. Эта недостача в определенной мере учитывается коэффициентом .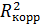

Многофакторный регрессионный анализ решает три задачи:

1) определяет специфику модели – вид функции неслучайных переменных 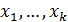, включенных в модель;

2) выявляет тесноту связи между факторами;

3) устанавливает влияние отдельных факторов на результативный признак.

При отборе факторов модели представляет интерес матрица коэффициентов парной корреляции

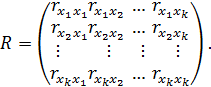
В случае линейной зависимости множественной регрессии исследуется так же расширенная матрица

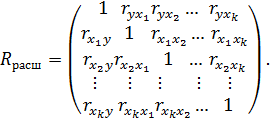
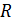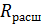Элементы матриц и позволяют сделать отбор факторов и определить их минимальное, но достаточное количество для описания результативной переменной.

Многофакторная модель линейной регрессии может быть представлена как

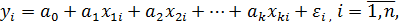
или в матричном ви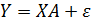де , где

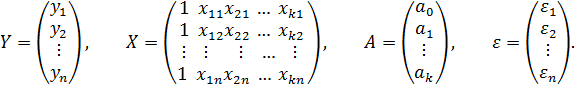
Факторы, включаемые в модель, должны быть количественно измеримы. Так, если фактор изначально качественный, то ему нужно придать количественную определенность. Подобная ситуация возникает, когда при построении регрессионных моделей помимо количественных переменных необходимо отразить и некоторые атрибутивные признаки (регион, образование, пол и т.д.). Такого рода переменные называются качественными или фиктивными. Они отражают неоднородность статистической совокупности и используются для более качественного моделирования по совокупности неоднородных объектов наблюдения. Учет влияния фиктивных переменных осуществляется с помощью булевых переменных, которые могут принимать только одно из двух возможных значений: 0 или 1.

Однако в некоторых случаях бывает целесообразно разделить неоднородную совокупность на однородные и применять моделирование к отдельным однородным совокупностям данных.

Пример.Пусть эконометрическая модель включает такие факторы: а) пол работника (мужской, женский); б) уровень образования (среднее, высшее); в) категория жилья (общежитие, отдельная квартира); г) социальный статус (замужем, не замужем); д) стаж работы (лет, месяцев); е) среднемесячная зарплата; ж) величина прожиточного минимума в регионе. Какие из этих факторов являются количественными, а какие качественными?

Ответ. Первые четыре фактора являются качественными, поскольку не могут быть измерены. Последние три, напротив, могут быть измерены и потому являются количественными.

Пример. При продаже-покупке квартиры в городе ее цена y может зависеть от полезной площади xи таких качественных факторов как: 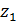– дом кирпичный, 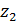– дом панельный. Придадим качественным (фиктивным) переменным количественное значение:

Теперь уравнение регрессии можно представить в виде 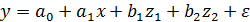. Пусть теоретическая функция регрессии (цена квартиры) имеет вид 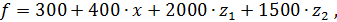тогда цены отдельных типов квартир даются формулами: 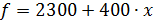– дом кирпичный; 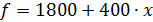– дом панельный.

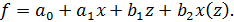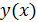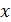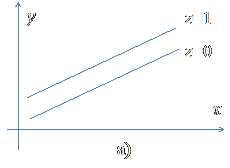
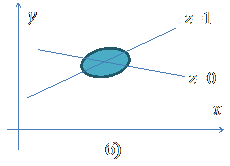
Важное требование, предъявляемое к эффективности линейной эконометрической модели, состоит в том, что взаимодействия фактора xи фиктивных переменных быть не должно. В противном случае анализ зависимости результата от факторов сильно усложняется, а уравнение регрессии принимает вид Аппроксимация зависимости при корреляции и фиктивной переменной 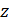весьма затрудняется. Эту ситуацию можно проиллюстрировать, см. рис. а) и б).

На рисунке а) схематически представлена зависимость результативного признака yот x при отсутствии связи между x и z, а на рисунке б) – при наличии такой связи.

Факторы, включаемые в модель должны быть некоррелированы. При сильнойинтеркорреляции объясняющих факторов, когда 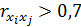, невозможно определить их раздельное влияние на результативный признак. В этом случае характеристики уравнения регрессии плохо интерпретируются, а их оценки ненадежны. Так, в уравнени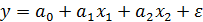и , при 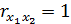с изменением 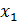будет меняться и 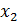. 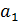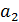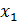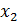Тогда и нельзя интерпретировать как показатели силы раздельного влияния и на 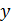. Дублирующие факторы из модели необходимо исключить. Из двух факторов 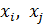, для которых 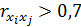, исключить следует тот, который имеет менее выраженный экономический смысл и слабее связан с результативным признаком y.

Отбор факторов модели осуществляется в два этапа:

1) включаются факторы, исходя из экономической природы явления, а экономически немотивированное включение в модель факторов – нецелесообразно;

2) на основе анализа корреляционной матрицы исключаются дублирующие факторы, т.е. факторы, имеющие неслучайную связь с уже отобранными.

Следует понимать, что матрица коэффициентов парной корреляции позволяет исключить лишь явнуюколлинеарность двух факторов.

В случае линейной зависимости между факторами и результативной переменной анализ корреляционной матрицы и выборочных коэффициентов множественной корреляции исчерпывает анализ мультиколлинеарности.