Оценка значимости параметров и качества модели

Пусть эмпирическое уравнение регрессии имеет вид . Перепишем это уравнение в виде . – отклонение результатаi-го наблюдения от среднего значения независимой переменной y;

– отклонение линии регрессии в наблюдаемойi-й точке от среднего значения ;

–отклонение результатаi-го наблюдения отмодельного значения, определяемого по линии регрессии в точке x_i.

Прямая является одной из возможных,для которых выполняется условие . Таким образом, коэффициент детерминации позволяет определить в какой степени прямая найденная по МНК дает лучший результат для объяснения зависимой переменной yчем горизонтальная прямая .

Возведем обе части переписанного уравнения регрессии в квадрат и просуммируем, тогда получим

Можно показать (покажите), что . Тогда при анализе статистической модели общую дисперсиюокончательно рассматривают как сумму объясненной и остаточной дисперсий:

Общая сумма квадратов отклонений = сумма квадратов отклонений, объясненная регрессией + остаточная сумма квадратов отклонений.

Сумма квадратов отклонений связана с числом степеней свободы n варьирования признака. Число же степеней свободы связано с объемом выборки n(величиной совокупности).

Общая сумма квадратов интерпретируется как мера общего разброса зависимой переменной yотносительно . Для образования общей суммы квадратов отклонений (левая часть дисперсионного равенства) из nвозможных отклонений: свободно варьируются только отклонений. Поскольку все значения 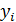связаны условием , то одно (любое) из nотклонений является следствием остальных отклонений. Таким образом, для вычисления левой части суммы квадратов необходимо только отклонений (независимых вариаций). Итак, число степеней свободы (в однофакторной модели) общей дисперсии равно . Объясненная сумма квадратов интерпретируется как мера разброса, объясненная с помощью регрессии; она имеет только одну степень свободы. Действительно, поскольку при заданном наборе , рассчитываемое значение , является лишь функцией коэффициента регрессии 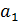в силу связи , то . Что касается количества степеней свободы суммы квадратов случайной переменной , то в общем случае, мы о нем ничего сказать не можем.

В случае однофакторной модели линейной регрессии имеет место теорема о равенстве степеней свободы общей суммы квадратов сумме квадратов факторной и остаточной составляющих: . Отсюда, число степеней свободы остаточной суммы квадратов составляет .

Средние квадраты отклонений или дисперсиив однофакторной моделив расчете на одну степень свободы даются формулами:

Здесь и далее через S² обозначается дисперсия в расчете на одну степень свободы, в отличие от средней по совокупности дисперсии s².

Чем меньше остаточная дисперсия, тем меньше влияние неучитываемых в модели факторов и тем лучше модель регрессии подходит к исходным данным. Отношение факторной (объясненной) и остаточной (необъясненной) дисперсий в расчете на одну степень свободы позволяет сделать вывод о значимости (существенности) уравнения регрессии в целом. Так, если

то нулевая гипотеза 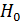об отсутствии связи признаков отклоняется и уравнение регрессии признается значимым.

Для малых выборок средние ошибки случайных отклонений даются формулами:

Надежность оценок коэффициента корреляции 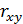и коэффициентов 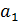и 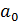в модели линейной регрессии 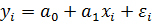зависит от их средних квадратических отклонений (случайных ошибок) и определяется с помощью критерия Стьюдента.

Расчетные значения

сравниваются, с определенным по таблице, при уровне значимости и числе степеней свободы значением . В частности, .

Замечание. При оценке надежности параметров регрессии можно использовать грубое правило: если стандартная ошибка больше модуля, исследуемого параметра, то он не может быть принят как значимый.

В парной линейной регрессии . Действительно, поскольку факторную сумму квадратов можно представить в виде , а остаточную сумму квадратов как – , то . Кроме того . Таким образом, .

Так как , , , то признается значимость коэффициента корреляции 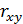и неслучайная природа коэффициентов 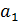и .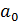

Для построения доверительных интервалов необходимо вычислить предельные ошибки оцениваемых величин. Поскольку , , имеют одно и то же распределение Стьюдента, то предельные ошибки, очевидно, даются соотношениями

, .

После решения вопроса о значимости коэффициента корреляции 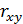, коэффициентов 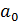, 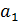и уравнения регрессии в целом можно установить доверительные интервалы этих величин в генеральной совокупности. Для каждого показателя имеем:

Доверительные вероятности параметров регрессии можно представить в виде

5 этап. Оценим точность модели вычислением среднего относительного отклонения расчетных данных от фактических. Допустимый предел значений должен быть не более 10%. Вычисляем относительную ошибку аппроксимации

Модель хорошо отражает зависимость между изучаемыми факторами xиy, если ошибка менее 10%. В нашем случае, средняя относительная ошибка аппроксимации, как мера рассеяния эмпирических точек вокруг теоретической линии регрессии меньше 10%, что говорит о высокой точности модели и свидетельствует о достаточном объеме выборки. Для повышения точности модели, количество наблюдений следует увеличить.

6 этап. Полученные оценкипараметров , при условии значимости их величин, позволяют использовать уравнение регрессиидля прогноза.

Обозначим через значение прогнозируемого показателя для фактора , тогда используя формулу для того же фактора, мы допускаем ошибку Здесь , определяемые по неизвестной нам генеральной совокупности коэффициенты. Поскольку оценки являются реализациями случайных величин-выборок, то наблюдаемая ошибка прогноза так же является реализацией случайной величины. При этом имеются дваисточника неопределенности ошибки прогноза: 1) отклонения от значений, вычисленных по генеральной совокупности; 2) неопределенность ошибки .

Если выполнены предпосылки МНК (мы это предполагаем), то имеет место соотношение

верное в силу несмещенности оценок параметров регрессии , , . Точность прогноза зависит от дисперсии ошибки прогноза

Здесь учтено, что – неслучайная (хотя и не известная) величина.