Спецификация моделей регрессии

Спецификация эконометрической модели включает: определение цели моделирования; определение списка переменных модели; разделение переменных на экзогенные – независимые, управляемые и планируемые, задаваемые извне автономно от модели и эндогенные -зависимые, формируемые внутри системы; обоснование вида уравнения модели (линейная, нелинейная, однофакторная, многофакторная).

В экономических процессах факторные признаки могут быть как детерминированными, так и стохастическими. Для классической эконометрической модели они всегда предполагаются заданными.

Независимые переменные, обусловливающие изменения других, называют так же факторными признаками (факторами), а объясняемые зависимые переменные – результативными.

Наиболее часто ошибка спецификации модели связана с неправильным выбором аналитической функции и недоучетом в уравнении регрессии некоторого существенного фактора. Ошибкой спецификации будет так же использование парной регрессии вместо множественной.

Рассмотрим совокупность всех теоретически возможных значений, связанных величин xиy, пишут так же 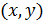. Группу – называют факторными экзогенными признаками, а группу – результативными эндогенными признаками.

Зависимости между факторными и результативными признаками можно разделить на две категории: 1) функциональные (линейные, нелинейные); 2) корреляционные (однофакторные, многофакторные). Функциональная зависимость дает точное соответствие между фактором и результатом. К функционально связанным экономическим факторам можно отнести, например, цену товара и выручку от его реализации. Корреляционная зависимость не дает точного соответствия между фактором и результатом. Воздействие фактора на результат проявляется лишь при массовом наблюдении – в среднем. При корреляционной зависимости устанавливается лишь тенденция изменения результативного признака под воздействием факторного. К корреляционно связанным экономическим факторам можно отнести, например, затраты на рекламу некоторого товара и выручку от его реализации.

Основной задачей корреляционного анализа является установление связи между случайными переменными 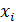– факторами модели и экономическим результатом y. Для этого проводится оценка тесноты связи, путем вычисления и последующего анализа коэффициентов парной корреляции, а так же проверка значимости или достоверности параметров модели и всего уравнения в целом. Корреляция не выясняет причину связей между факторами, а только устанавливает численное значение этих связей.

Регрессиейв математической статистике принято называть зависимость среднего значения какой-либо величины y от некоторойдругой величины или от нескольких величин х_i.Если у взаимосвязанных величин вариацию имеет только одна переменная, а другая (другие) является детерминированной, то такую связь называют не корреляционной, а регрессионной.Основной задачей регрессионного анализа является построение уравнения регрессии.

В условиях нормально распределенной генеральной совокупности (а это мы всегда предполагаем) при выборке объема 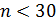нормированное отклонение выборочной средней от генеральной средней и соответствующая вероятность, подчинены закону распределения Стьюдента. В частности, для рассмотренного выше коэффициента корреляции 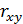, его среднеквадратическое отклонение 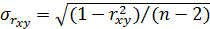подчинено закону распределения Стьюдента, здесь – выборочное значение коэффициента корреляции. Для выборки с 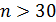c увеличением n распределение Стьюдента асимптотически приближается к нормальному так, что , . Т.е. математическое ожидание и дисперсия, оцениваемой характеристики, приближаются к своим значениям по генеральной совокупности.

Вопросы для обсуждения

1. Охарактеризуйте предмет эконометрики.

2. Какие задачи решают корреляционный и регрессионный анализы?

3. Какие зависимости называются стохастическими?

4. Какие типы данных используются в эконометрическом исследовании?

5. Опишите основные этапы построения эконометрической модели.