Распределение оценок для малых выборок

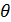Даже, если оценка некоторой характеристики по данным выборки: несмещена, состоятельна и эффективна – она все равно является лишь приближенным значением истинной характеристики . Госсет, известный под псевдонимом – Стьюдент, в 1908 году, установил закон распределения оценок для малых выборок. Этот закон называется законом Стьюдента. Таким образом, оценки характеристик (параметров), полученных на основе малых выборок, подчиняются статистике Стьюдента. Статистикой называют распределение выборочной характеристики 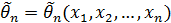, под которой понимают всякую функцию результатов наблюдений над случайной величиной x,по которой судят о значении оценки 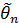характеристики .

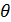Как правило, исследователь работает с выборочной совокупностью случайных переменных. Далее только ее и будем иметь в виду. Однако выборка должна быть репрезентативной, представительной и настолько большой, насколько это возможно и насколько этого требует качество решаемой задачи.

Средняя величина ошибки характеристики зависит от объема выборки n, вариации, изучаемой характеристики в генеральной совокупности и способа отбора. Выборка объема 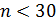считается малой. В условиях малой выборки дисперсия по выборочной совокупности может оказаться сильно смещенной и не может рассматриваться в качестве оценки дисперсии по генеральной совокупности. Приведем краткие сведения о статистике Стьюдента.

Распределением Стьюдента называется случайная величина:

где – случайная величина, распределенная по нормальному закону , а – не зависящая от случайная величина, имеющая -распределение с степенями свободы. есть распределение суммы квадратов независимых случайных величин , распределенных по закону . Напомним, что распределение случайной величины называется нормальным с параметрами и , т.е. ), если соответствующая ей плотность вероятности дается формулой: , где 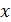– значение изучаемой характеристики.

Плотность вероятности хи-квадрат распределения имеет вид:

Распределение хи-квадрат асимптотически нормально:

где имеет распределение . Это означает, что при достаточно большом объеме выборки n можно приближенно считать . Фактически это соотношение выполняется уже при . Плотность вероятности распределения Стьюдента имеет вид:

Вероятность того, что нормированное отклонение выборочной средней от генеральной средней не превысит t, будет равна площади, ограниченной кривой распределения Стьюдента в интервале от до t:

Из формулы видно, что в условиях малой выборки вероятность появления ошибки зависит как от t так и от объема выборки, поскольку .

Распределение Стьюдента при увеличении объема выборки n приближается к нормальному распределению . При 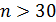расхождения в распределении Стьюдента и Гаусса – невелики.

Замечание. При распределение Стьюдента называется распределением Коши:

Математическое ожидание и дисперсия случайной величины с плотностью распределения Коши не существует в силу того, что

В то же время, для всех : . При : .