ТЕМА III – ЛОГИЧЕСКАЯ ОРГАНИЗАЦИЯ МАТЕМАТИЧЕСКОГО МАТЕРИАЛА.

Понятие математической деятельности человека.

Этапы развития научной теории.

Математическое понятие, его свойства

Определение математического понятия

Понятие математической деятельности человека.

При обучении детей математике целесообразно придерживаться концепции формирования и развития мыслительной деятельности определенной структуры – математической деятельности. Исследования показывают, что любой учащийся способен осуществлять математическую деятельность, адекватную его уровню мышления.

Математическая деятельность проявляется с первых шагов знакомства его с множествами: установление взаимно – однозначного соответствия между элементами двух множеств, определение числа элементов во множестве, осуществление операции объединения двух непересекающихся множеств. От операций с конкретными множествами (А 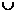В=С) учащийся переходит к операциям с числами (a+b=c) (отвлекаясь от конкретных предметов), осуществляется математическая деятельность на более высоком уровне. Далее, например, от формулировки переместительного закона сложения для конкретных чисел (2+3=3+2) переходят к обобщенному понятию этого закона (a+b=b+a) - это математическая деятельность на еще более высоком уровне. Приведенные примеры показывают, что для усвоения конкретного понятия математическая деятельность учащегося проходит определенные этапы своего развития.

Для того, чтобы помочь учащемуся правильно осуществлять математическую деятельность при изучении математики, учителю самому необходимо разобраться в логической структуре науки математики.

Ученые заметили, что некоторые конкретные системы, несмотря на свое видимое различие, имеют много общего в отношениях между своими объектами и свойствах отношений. Рассмотрим простой пример.

Пример 1.

1). Выберем объекты исследования:

Множество натуральных чисел: N={1,2,3,…n…}

Множество множеств: М={ }

2). Введем операции с элементами в каждом множестве:

Сложение натуральных чисел: a+b

Объединение множеств:

3). Введенные операции во множествах M и N обладают свойствами:

1) a+b=b+a –переместительное 2) (a+b)+c=a+(b+c) - сочетательное

1) - переместительное 2) - сочетательное

4). Введем отношения в множествах N и M:

Равенство натуральных чисел: а=b

Равносильность множеств:

5). Введенные отношения во множествах M и N обладают свойствами:

1) a=а – рефлексивности отношения равенства; 2) (а=b) (b=a) – симметричности отношения равенства; 3) - транзитивности отношения равенства.

1) - рефлексивности отношения равносильности; 2) - симметричности отношения равносильности; 3) - транзитивности отношения равносильности.

Рассмотренный пример показывает, насколько сходны свойства некоторых операций и некоторых отношений во множествах различной природы. Такого рода свойства отношений, структуру связей математических объектов ученые абстрагируют и изучают.