Задачи математической статистики
Статистические данные представляют собой данные, полученные в результате обследования большого числа объектов или явлений; следовательно, математическая статистика имеет дело с массовыми явлениями.Первая задача математической статистики - указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов.Вторая задача математической статистики - разработать методы анализа статистических данных в зависимости от целей исследования. задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов.Генеральной (основной) совокупностью называют совокупность, объектов из которых производится выборка.Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности.
Способы выборкиПовторная называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.Бесповторная называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.
2. Дисперсия дискретной случайной внличины и ее свойстваДисперсией дискретной случайной величины X называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D(X)=M(X-M(X))^2.
СвойстваD(C)=0_D(CX)=C^2D(X)_D(X+Y+Z)=D(X)+D(Y)+D(Z)_D(C+X)=D(X)
Билет№ 16
Классификация уравнений второго порядка
Линейные уравнения второго порядка в частных производных подразделяют на параболические, эллиптические и гиперболические.
Линейное уравнение второго порядка, содержащее две независимые переменные, имеет вид:
где A, B, C — коэффициенты, зависящие от переменных x и y, а многоточие означает члены, зависящие от x, y, u и частных производных первого порядка: 
и 
. Это уравнение похоже на уравнение конического сечения:
Так же, как конические сечения разделяются на эллипсы, параболы и гиперболы, в зависимости от знака дискриминанта 
, классифицируются уравнения второго порядка в заданной точке:
1. 
— Гиперболическое уравнение,
2. 
— Эллиптическое уравнение,
3. 
— Параболическое уравнение
16.2 Равновозможные – если каждое событие в силу симметрии опыта не более возможно, чем остальные. Пространство элементарных событий Ω – множество всех элементарных событий, исходов. Исходы, составляющие событие, - благоприятствующие данному событию. . Классическое определение вероятности:
Пусть пространство Ω – полная группа равновозмож-ных n исходов. Ω={w1,w2…wn}. Пусть событие А состоит из m исходов А={wi1,wi2…wim}. Тогда вероятностью Р(А) события А считают отношение m благоприятных исходов к числу n всех исходов опыта
P(A)=m/n
Свойства вероятности:
0<=P(A)<=1
P(Ω)=1
P(Ø)=0
Билет№2
1. Возведение в степень. Формула Муавра
При возведении комплексного числа в любую целую степень модуль комплексного числа возводится в ту же степень, а аргумент умножается на показатель степени.
Zª=rª(cosAφ+i*sin Aφ)
Данная формула называется формулой Муавра. Она верна и для целого отрицательного значения n, а также для n = 0.
2.Математическое ожидание случайной величины
Математическое ожидание - число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание случайной величины обозначается M .
Математическое ожидание дискретной случайной величины , имеющей распределение
| x1 | x2 | ... | xn |
| p1 | p2 | ... | pn |
называется величина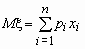 
, если число значений случайной величины конечно.
Если число значений случайной величины счетно, то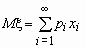 
. При этом, если ряд в правой части равенства расходится, то говорят, что случайная величина не имеет математического ожидания.
Математическое ожидание непрерывной случайной величины с плотностью вероятностей p(x) вычисляется по формуле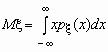 
. При этом, если интеграл в правой части равенства расходится, то говорят, что случайная величина не имеет математического ожидания.
Если случайная величина является функцией случайной величины , = f(x), то
.
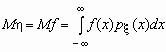Аналогичные формулы справедливы для функций дискретной случайной величины:
, 
.
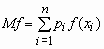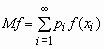Билет №10
Медиана — это такое значение признака, которое разделяет ранжированный ряд распределения на две равные части — со значениями признака меньше медианы и со значениями признака больше медианы. Для нахождения медианы, нужно отыскать значение признака, которое находится на середине упорядоченного ряда.
В ранжированных рядах несгруппированные данные для нахождения медианы сводятся к поиску порядкового номера медианы. Медиана может быть вычислена по следующей формуле:
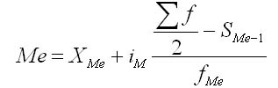
где Хm — нижняя граница медианного интервала;
im — медианный интервал;
Sme— сумма наблюдений, которая была накоплена до начала медианного интервала;
fme — число наблюдений в медианном интервале.